Приклад розв’язання другої задачі динаміки

Розглянемо так звану задачу балістики. Із точки О у вакуумі вилітає матеріальна точка маси m зі швидкістю 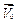, що утворює із горизонтом кут (рис.2.12). Знайти закон руху точки.

Розв’язання.

1) Оберемо спосіб задання руху точки. Векторний спосіб задання руху застосовуютьо тільки при доведенні теорем. Натуральний спосіб задання руху використовують лише у тому випадку, коли відома траєкторія точки. В нашій задачі необхідно знайти траєкторію точки, тому натуральний спосіб завдання руху застосувати не можна. Обираємо координатний спосіб задання руху. Початок координат розташуємо у точці О, вісь Ox направимо горизонтально, вісь Oy – вертикально вгору.

2) Проаналізуємо сили, які діють на точку. Розглянемо довільне положення точки М на траєкторії. На точку діє сила тяжіння . Силою опору нехтуємо.

Якщо б на точку не діяла сила тяжіння, вона рухалась би по прямій, що співпадає із напрямком . Точка М рухається у площині Оxy, тому складемо два диференціальних рівняння руху

; . (а)

Спростимо рівняння (а):

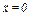; . (b)

Інтегруємо рівняння (b) :

; (с)

Інтегруючи ще раз, отримаємо :

x = ; y = - ; (d)

Сталі інтегрування знайдемо із початкових умов руху:

при t=0 , , 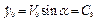, 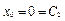. Тоді закон руху матеріальної точки матиме вигляд:

x = 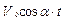; y = - .

2.1.4. Вільні та невільні системи матеріальних точок. В'язі та їх реакції

Системою матеріальних точок називається сукупність матеріальних точок, положення і рух яких пов'язані між собою.

Всі тіла, які ми бачимо навколо себе можна розглядати, як системи матеріальних точок. Розрізняють вільні та невільні системи матеріальних точок.

Вільними називаються такі матеріальні об'єкти, на рух яких не накладені наперед задані обмеження. І навпаки.

В'язями називають тіла, які обмежують свободу руху точок матеріальної системи безпосереднім контактом з її точками.

Це визначення є нестрогим. Тому при характеристиці в'язі частіше за все звертаються до її аналітичного визначення. Кожну в'язь можна описати рівнянням.

Сила, з якою в'язь діє на матеріальний об'єкт називається реакцією в'язі і відноситься до сил пасивних, на відміну від сил активних або тих, що задаються.

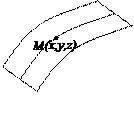
рис.2.13

Розглянемо деякі приклади. Поверхня, по якій рухається точка М, є для неї в'яззю (рис.2.13). Якщо рівняння поверхні можна представити у вигляді

f(x, y, z)=0, (2.13)

в'язь називається стаціонарною. В рівняння в'язі час явно не входить, поверхня нерухома.

Якщо поверхня рухається, в рівняння поверхні входить час f(t, x, y, z)=0, (2.14)

в'язь називається нестаціонарною.

Якщо в рівняння в'язі не входять проекції швидкостей точок системи, то в'язь називається геометричною. Якщо ж в'язь задається рівнянням виду

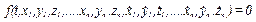, (2.15)

то вона називається нестаціонарною кінематичною.

рис.2.14	рис.2.15

Як приклад в'язі можна розглянути дріт, по якому рухається кільце М (рис.2.14). Криву АВ можна розглядати як перетин двох поверхонь. В'язь АВ характеризується двома рівняннями:

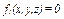, . (2.16)

Розглянемо рух точки М, прикріпленої до пружини (рис.2.15). Рух пружини залежить від закону руху точки М. В цьому випадку в'язь неможливо описати рівнянням руху точки М, тому її можна вважати вільною.

Повернемося до розгляду вільних систем матеріальних точок. Система матеріальних точок називається вільною, якщо на рух її точок не накладені наперед задані, тобто незалежні від закону руху обмеження. Прикладом вільної системи матеріальних точок є сонячна система, якщо комети, планети, Сонце розглядати як матеріальні точки. Таке уявлення про сонячну систему введено Ньютоном. Закони Ньютона справедливі лише для вільних матеріальних об'єктів.

Як про курйоз можна згадати про уявлення Птоломея про всесвіт, за яким центром всесвіту вважалася Земля, а Сонце, зірки та планети рухалися навколо Землі за допомоги системи коліс. Птоломей вважав сонячну систему невільною.

Система матеріальних точок називається невільною, якщо на рух точок системи накладені в'язі.

На земній поверхні спостерігається взаємодія тіл при їх русі. Тому всі тіла, які ми спостерігаємо навколо себе, є прикладом невільних систем. Виникає питання, як використати закони Ньютона, знайдені ним для вільних систем, для вивчення систем невільних? Різницю між вільними та невільними системами можна усунути, вводячи аксіому про звільнення від в'язей.