Центр мас, кількість руху системи матеріальних точок

Надамо формулам (2.25) і (2.26) вигляд, більш зручний для практичного застосування при розв'язанні задач.

Розглянемо рух точок системи відносно нерухомого центра 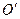як складний, що складається із поступального руху разом із рухомими осями 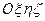і руху відносно цих осей (рис.2.21). Тоді на основі теореми про

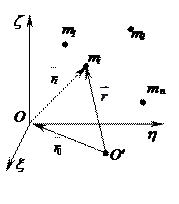
складання швидкостей абсолютна швидкість i–тої точки системи рівна

рис.2.21

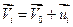(а)

де 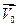– швидкість поступального переносного руху, рівна швидкості початку рухомої системи координат; 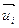– швидкість відносного руху .

Кінетичну енергію системи, взявши до уваги (а), можна виразити наступним чином:

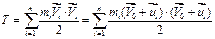. (b)

Виконавши перетворення, отримаємо

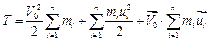. (с)

При раціональному виборі точки О – початку рухомої системи координат 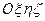вираз (с) можна спростити, виключивши із нього третій доданок.

Дійсно,

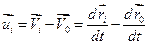. (d)

Далі

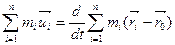. (е)

Визначимо початок рухомої системи координат, прирівнявши до нуля суму, що стоїть у правій частині рівності (е):

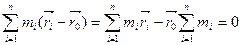. (f)

Звідки

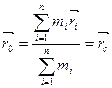. (2.28)

Точка положення якої визначається радіус-вектором 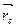, називається центром мас, або центром інерції матеріальної системи. За іншим визначенням, центр мас - це центр паралельних сил, що надають рух точкам системи з однаковим прискоренням або поступальний рух незмінній системі.

Рух системи матеріальних точок відносно осей координат, які рухаються поступально разом з центром мас, називається рухом відносно центра мас.

Сума мас окремих точок системи називається масою системи

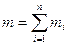. (2.29)

Рівність (с) при виборі початку рухомої системи координат у центрі мас можна записати так :

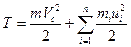. (2.30)

Рівність (2.30) виражає теорему Кеніга: кінетична енергія системи матеріальних точок рівна кінетичній енергії поступального руху системи разом з її центром мас, що складена з кінетичною енергією системи відносно центра мас.

Теорема Кеніга підтверджує, що основні властивості системи містяться у виразі її кінетичної енергії.

Із поняттям про центр мас зв’язано поняття про кількість руху системи.

Із рівностей (2.28) і (2.29) випливає:

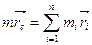. (g)

Продиференціювавши цю рівність за часом, отримаємо вираз для кількості руху системи:

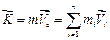. (2.31)

Кількість руху системи матеріальних точок рівна векторній сумі кількостей руху всіх точок системи . Із (2.31) видно, що кількість руху системи можна підрахувати як добуток маси системи на швидкість її центра мас.

В залежності від способу руху матеріальної системи різняться і вирази для кінетичної енергії.

1. При поступальному русі 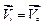, тоді:

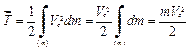
2. При обертальному русі.

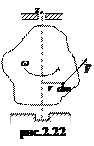
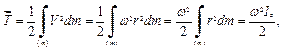
де 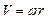- модуль формули Ейлера, а 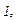- осьовий момент інерції

3. При плоско-паралельному русі.

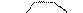
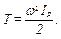
причому 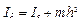. Тоді

.

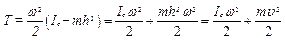2.1.7. Основні властивості довільної системи сил, які діють на абсолютно тверде тіло

Елементарна робота сил, які діють на абсолютно тверде тіло

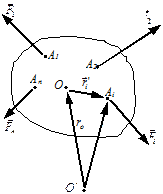
Щоб практично використовувати теорему про зміну кінетичної енергії, потрібно вміти обчислювати роботу сил, прикладених до абсолютно твердого тіла. Розглянемо тверде тіло, на яке діє система п сил (рис.2.24). Знайдемо суму елементарних робіт, які виконують сили на елементарних переміщеннях. Елементарна робота і-ї сили дорівнює

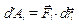. (а)

рис.2.24.

Оберемо в тілі полюс – точку О. З нерухомої точки O', розташованої поза тілом, проведемо радіус-вектори в довільну точку тіла А_і та в полюс О. З рис.2.24 видно, що .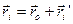

Звідки

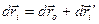(b)

Підставимо (b) в (а), знайдемо

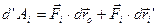.(с)

З кінематики відомо, що швидкість будь-якої точки тіла дорівнює

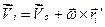. (d)

де 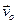- швидкість полюсу, 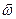- миттєва кутова швидкість обертання тіла навколо полюса. Вираз (d)можна представити інакше:

.

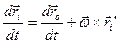Помноживши на dt обидві частини рівняння, отримаємо

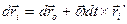. (е)

Тут 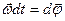- елементарний кут повороту навколо осі, що проходить через точку О та змінює своє положення в просторі з часом. Прийнявши це позначення, представимо формулу (е) у вигляді

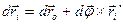. (f)

Порівнюючи (b) та (f), знайдемо

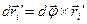. (g)

Підставимо (g) в (с), отримаємо

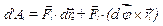. (h)

З аналітичної геометрії відомо, що скалярно-векторний добуток рівний об'єму паралелепіпеда, побудованого на векторах-множниках. В паралелепіпеді будь-яку грань можна розглядати, як основу, тому в скалярно-векторному добутку можна змінювати множники за правилом циклічної перестановки. Другий доданок в (h) можна переписати так:

,

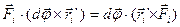після чого формула (h) приймає вигляд:

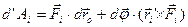. (і)

Щоб знайти повну роботу, що виконують сили, які діють на абсолютно тверде тіло, треба просумувати роботи, виконані кожною силою:

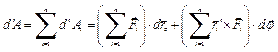. (j)

Векторна сума сил, діючих на абсолютно тверде тіло, називається головним вектором системи сил

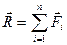. (2.32)

Векторний добуток, який стоїть під знаком другої суми, позначається

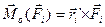(2.33)

та називається моментом сили 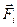відносно точки О.

Векторна сума моментів сил відносно точки О, що позначається

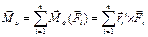, (2.34)

називається головним моментом сил відносно точки О. Точка О є центром моментів.

Підставимо в (j) вирази (2.32) та (2.34), отримаємо

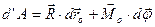. (2.35)

Рівність (2.35) виражає теорему про роботу сил, які діють на абсолютно тверде тіло: елементарна робота довільної системи сил, прикладених до абсолютно твердого тіла, дорівнює сумі двох доданків – елементарній роботі, що виконується головним вектором системи сил на поступальному переміщенні тіла разом с полюсом, складеній з елементарною роботою, що виконується головним моментом системи сил на обертальному переміщенні тіла навколо полюса.

Теорема про зміну кінетичної енергії матеріальної системи. Приріст кінетичної енергії системи матеріальних точок за деякий проміжок часу дорівнює сумі робіт зовнішніх і внутрішніх сил, що діють на точки системи протягом того ж проміжку часу. Доведемо цю теорему.

За теоремою про зміну кінетичної енергії для і-ої точки матеріальної системи маємо

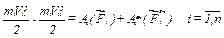
Виходячи з означення кінетичної енергії системи маємо:

,

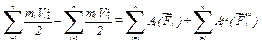тоді .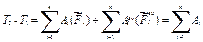

Статика

Статикою називається розділ теоретичної механіки, в якому вивчаються способи перетворення систем сил в інші, що еквівалентні їм, а також умови рівноваги різних систем сил, які діють на абсолютно тверде тіло.

Одним з основних понять статики є сила.

Сила - це міра взаємодії між тілами, яка має напрямок, величину і точку прикладання.