Теорема про зміну кінетичної енергії системи матеріальних точок

Кінетичною енергією системи матеріальних точок називається сума кінетичних енергій точок , що створюють систему :

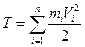. (2.25)

Якщо система являє собою неперервне середовище, то, розбиваючи його на n елементів маси 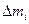, знайдемо наближено кінетичну енергію

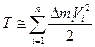(а)

де 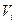– швидкість внутрішньої точки елемента 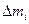. Покладемо, що елемент надзвичайно малий і швидкості всіх його точок наближено однакові.

Щоб знайти точне значення кінетичної енергії неперервного середовища, збільшимо число елементів n до нескінченності, стягуючи кожний в точку. Після граничного переходу отримаємо

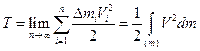(2.26)

Розповсюдимо теорему про зміну кінетичної енергії на систему матеріальних точок: зміна кінетичної енергії системи матеріальних точок за деякий проміжок часу дорівнює роботі, що створюється силами, що діють на точки системи за той же проміжок часу.

Розглянемо систему, що складається із n дискретних точок із масами 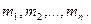У кожній точці системи можна застосувати теорему про зміну кінетичної енергії. Для і-тої точки системи можна записати:

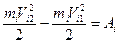(b)

Просумуємо рівність (в) за числом точок у системі. Отримаємо

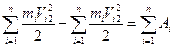. (с)

На підставі (2.25) надамо формулі (с) вигляд

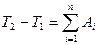(2.27)

де 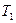і 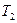– кінетична енергія системи у початковий і кінцевий моменти часу. Рівність (2.27) виражає теорему про зміну кінетичної енергії системи матеріальних точок .

Щоб застосувати теорему до розв'язання задач, потрібно вміти обчислювати кінетичну енергію систем твердих тіл для різних випадків їх рухів.