Еквівалентні системи сил. Елементи статики

З формули (2.35) видно, що елементарна робота сил, діючих на абсолютно тверде тіло, залежить від головного вектора та головного моменту системи сил. Звідси випливає, що одну й ту ж елементарну роботу на однакових довільних переміщеннях можуть виконувати різні системи сил, при цьому вони викликатимуть однакову механічну дію, надаючи кінетичній енергії тіла однакові прирости.

Дві системи сил називаються еквівалентними, якщо вони виконують однакову елементарну роботу на довільних, але однакових переміщеннях абсолютно твердого тіла.

Покажемо, що еквівалентні системи сил мають однакові головні вектори та головні моменти.

Припустимо, що є дві системи сил з головними векторами та головними моментами 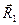, 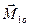; 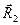, 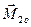. Доведемо, що головні вектори та головні моменти однакові, якщо ці системи еквівалентні.

Розглянемо елементарну роботу, яка виконується системами 1 та 2. За умовою системи сил еквівалентні, тому вони виконують одну й ту ж роботу:

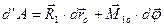,(а)

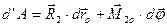.(b)

Віднімемо від рівності (b) рівність (а):

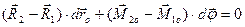. (с)

Рівність (с) має виконуватись при довільному переміщенні, та 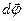довільні та незалежні.

Покладемо 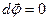, , 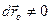тіло при цьому рухається поступально. Тоді рівняння (с) прийме вигляд

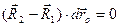(d)

Але вектор 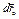довільний. Можна обрати його так, щоб він був паралельним різниці 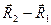. Тоді для виконання рівності (d) необхідно, щоб перший множник скалярного добутку (d) був рівний нулю:

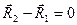або .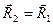

Аналогічно можна показати, що в еквівалентних системах мають бути рівними головні моменти .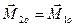

Якщо дві системи еквівалентні, то в них однакові головні вектори та головні моменти.