Миттєвий центр швидкостей та способи його знаходження.
Із (1.60) можна зробити висновок, що в кожний момент часу існує точка, для якої 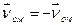 , тобто швидкість якої дорівнює нулеві. Цю точку називають миттєвим центром швидкостей (МЦШ).
, тобто швидкість якої дорівнює нулеві. Цю точку називають миттєвим центром швидкостей (МЦШ).
Отже, МЦШ – називається точка плоскої фігури швидкість якої дорівнює нулю в даний момент часу.
Якщо полюс вибрати в миттєвому центрі швидкостей, то на підставі (1.60) 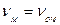 .
.
Швидкості точок плоскої фігури можна розглядати як швидкість її обертального руху навколо миттєвого центра швидкостей. Тому миттєвий центр швидкостей називають ще миттєвим центром обертання.
Найчастіше МЦШ позначають 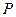 .
.
Розглянемо побудову миттєвого центра швидкостей. Для цього існує кілька способів.
1. Якщо відома швидкість 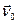 певної точки
певної точки 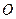 фігури і миттєва кутова швидкість
фігури і миттєва кутова швидкість 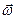 , то миттєвий центр
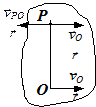
, то миттєвий центр 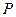 швидкостей (рис.1.24) знайдемо на прямій
швидкостей (рис.1.24) знайдемо на прямій 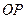 , перпендикулярній до
, перпендикулярній до 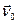 .
.
|
| рис. 1.24 |
Дійсно, виберемо 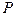 за полюс і знайдемо швидкість точки
за полюс і знайдемо швидкість точки 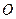 :
:
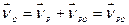 ;
;
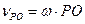 і
і 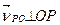 .
.
Звідси 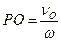 . (1.61)
. (1.61)
Миттєвий центр швидкостей лежить на прямій 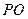 , перпендикулярній до вектора
, перпендикулярній до вектора 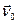 , на відстані
, на відстані 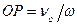 . Відрізок
. Відрізок 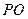 відкладається від точки
відкладається від точки 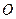 у напрямі, що визначається знаком вектора
у напрямі, що визначається знаком вектора 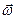 .
.
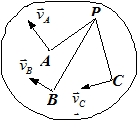
|
| рис.1.25 |
2. Нехай відомі прямі, уздовж яких напрямлені швидкості двох точок А і В плоскої фігури (рис.1.25), і відома швидкість точки 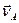 . Розглянемо швидкості
. Розглянемо швидкості 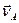 і
і 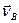 як швидкості обертального руху навколо миттєвого центра обертання. Ці швидкості мають бути перпендикулярні до радіусів обертання
як швидкості обертального руху навколо миттєвого центра обертання. Ці швидкості мають бути перпендикулярні до радіусів обертання 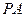 і
і 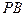 . Отже, проводимо
. Отже, проводимо 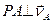 і
і 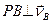 .
.
У точці їх перетину знаходиться миттєвий центр 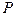 швидкостей. Застосувавши формулу (1.61), дістанемо:
швидкостей. Застосувавши формулу (1.61), дістанемо:
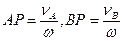
Звідси
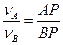 (1.62)
(1.62)
Відношення швидкостей двох точок плоскої фігури дорівнює відношенню їхніх відстаней від миттєвого центра швидкостей. Формулу (1.62) можна записати інакше:
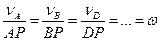 . (1.63)
. (1.63)
Установленими формулами широко користуються при розв’язуванні задач, у яких треба визначити швидкості точок тіла при плоскопаралельному русі (наприклад, точки D). Для цього досить з’єднати точку 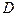 з миттєвим центром і провести перпендикуляр до
з миттєвим центром і провести перпендикуляр до 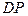 . Напрям швидкості
. Напрям швидкості 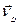 знаходимо згідно з напрямом обертання плоскої фігури навколо полюса. Модуль вектора
знаходимо згідно з напрямом обертання плоскої фігури навколо полюса. Модуль вектора 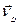 обчислюємо з пропорції (1.63).
обчислюємо з пропорції (1.63).
3. Існує ще кілька окремих випадків визначення миттєвого центра швидкостей:
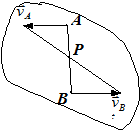
а) швидкості двох точок тіла паралельні, нерівні і мають один напрям (рис.1.26,а);
б) швидкості двох точок тіла паралельні, нерівні і мають різні напрями (рис.1.26,б);
в) швидкості двох точок тіла паралельні, рівні, напрямлені в один бік (рис.1.27). У цьому разі миттєва кутова швидкість 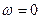 і тіло в цей момент часу виконує миттєвий поступальний рух;
і тіло в цей момент часу виконує миттєвий поступальний рух;
г) у деяких випадках можна знайти положення миттєвого центра швидкостей з умови кочення без ковзання: миттєвий центр знаходиться в точці дотику тіла з нерухомою поверхнею (рис.1.28).
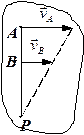
| 
|
| а | б |
| рис.1.26 | |
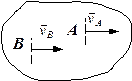
| 
|
| рис.1.27 | рис.1.28 |
Зауважимо, що під час руху тіла положення миттєвого центра швидкостей змінюється. Геометричне місце миттєвих центрів швидкостей, віднесене до рухомої або нерухомої системи координат, називають відповідно рухомою або нерухомою центроїдою. Центроїдою називається геометричне місце миттєвих центрів швидкостей. З цією геометричною інтерпретацією плоскопаралельного руху пов’язана теорема Пуансо.
Теорема Пуансо. Під час руху плоскої фігури рухома центроїда котиться по нерухомій без ковзання.
Наприклад, при кочені циліндра по горизрнтальній площині (рис. 1.28) нерухома центроїда – горизонтальна пряма, а рухома – коло. В кожний момент часу рухома і нерухома центроїди мають загаліну точку дотику – миттєвий центр швидкостей Р, тобто точку, швидкість якої дорівнює нулю.
Це окремий випадок більш загальної теореми Пуансон, яку ми будемо розглядати, вивчаючи обертання твердого тіла навколо нерухомої точки.
Нарешті, слід відмітити, що плоскопаралельний рух розглядали як окремий випадок руху вільного твердого тіла.
План швидкостей
Розглянемо графічний метод визначення швидкостей різних точок плоскої фігури. Це метод побудови плану швидкостей.
План швидкостей – це графічне зображення векторів швидкостей точок плоскої фігури в даний момент часу.
Для побудови плану швидкостей треба знати величину і напрям швидкості однієї точки, а також напрям швидкості якої-небудь іншої точки плоскої фігури.
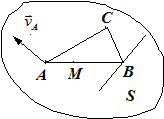
Визначимо швидкості всіх точок фігури 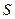 (рис.1.29), якщо відомі вектор швидкості
(рис.1.29), якщо відомі вектор швидкості 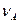 точки
точки 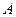 і те, що вектор
і те, що вектор 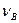 напрямлений вздовж прямої
напрямлений вздовж прямої 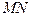 .
.
Скористуємося формулами (1.59) і (1.60). Визначимо спочатку швидкість точки В, напрям якої відомий. Виберемо полюс у точці А.
Тоді
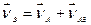 ; (а)
; (а)
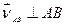 . (в)
. (в)
Побудуємо рівність (а). Вектор 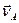 відомий цілком, а вектори
відомий цілком, а вектори 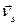 і
і 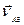 відомі за напрямом. Виберемо масштаб і побудуємо трикутник за відомою стороною
відомі за напрямом. Виберемо масштаб і побудуємо трикутник за відомою стороною 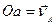 (рис. 1.30) і відомими напрямами двох інших сторін:
(рис. 1.30) і відомими напрямами двох інших сторін: 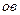 проводимо паралельно напряму
проводимо паралельно напряму 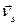 ,
, 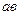 - перпендикулярно до
- перпендикулярно до 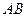 . Дістаємо
. Дістаємо
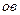 =
= 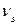 ;
; 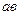 =
= 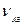 (c)
(c)
| 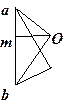
|
| рис.1.29 | рис.1. 30 |
Щоб визначити швидкість довільної точки С, з’єднаємо її з точками А та В. Маємо
 ; (d)
; (d)
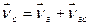 ; (e)
; (e)
Швидкість точки невідома; швидкості точок А та В повністю відомі; 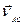 і
і 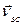 відомі за напрямом. Розв’язуємо графічно систему векторних рівнянь (d) і (е). На плані швидкостей через точки а і в проводимо прямі, паралельні швидкостям
відомі за напрямом. Розв’язуємо графічно систему векторних рівнянь (d) і (е). На плані швидкостей через точки а і в проводимо прямі, паралельні швидкостям 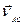 і
і 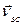 (відповідно перпендикулярні до прямих
(відповідно перпендикулярні до прямих 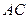 і
і 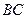 ):
): 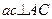 ,
, 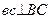 . Точка перетину
. Точка перетину 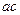 і
і 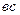 є точка С – кінець вектора
є точка С – кінець вектора 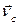 . З’днаємо точку С з точкою О. Швидкість точки С побудована (
. З’днаємо точку С з точкою О. Швидкість точки С побудована ( 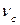 =
= 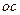 ).
).
Як видно із побудови, 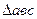 на плані швидкостей подібний до
на плані швидкостей подібний до 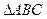 плоскої фігури і повернутий відносно нього на кут
плоскої фігури і повернутий відносно нього на кут 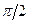 .
.
Тепер легко знайти швидкість будь-якої точки плоскої фігури. Наприклад, щоб знайти швидкість точки М, яка знаходиться на прямій АВ (див. рис. 1.29) визначимо відповідну їй точку 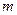 на плані швидкостей, з’єднаємо цю точку з полюсом
на плані швидкостей, з’єднаємо цю точку з полюсом 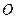 (
( 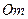 - швидкість точки М).
- швидкість точки М).
Положення точки 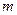 на плані швидкостей зручно визначати так:
на плані швидкостей зручно визначати так:
відрізки 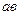 ,
, 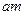 тощо на плані швидкостей є швидкості обертального руху
тощо на плані швидкостей є швидкості обертального руху 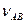 ,
, 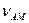 та ін. Відомо, що
та ін. Відомо, що 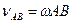 ,
, 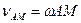 . Тому для визначення положення точки
. Тому для визначення положення точки 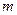 маємо співвідношення
маємо співвідношення
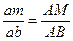 . (f)
. (f)
Із плану швидкостей можна визначити також миттєву кутову швидкість. На підставі (f) дістаємо
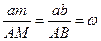 . (g)
. (g)
Дата добавления: 2020-08-31; просмотров: 1720;











