Плоскопаралельний рух твердого тіла. Рівняння руху
Плоскопаралельним називають такий рух твердого тіла, під час якого всі точки тіла рухаються паралельно певній нерухомій площині, яку називають основною.
Багато механізмів, які зустрічаються в практиці, належать до так званих плоских механізмів. Тому вивчення плоскопаралельного руху тіла має істотне практичне значення.
Плоскопаралельний рух можна розглядати як окремий випадок руху вільного твердого тіла.
Покажемо, що з означення плоскопаралельного руху випливає можливість звести задачу вивчення руху тіла в просторі до задачі вивчення руху плоскої фігури в площині.
Теорема. Будь-яке переміщення плоскої фігури в її площині може бути здійснено поступальним переміщенням разом з вибраним полюсом і обертальним рухом навколо вибраного полюса.
Тіло перебуває в плоскопаралельному русі (рис.1.21), площина 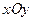 - основна.
- основна.
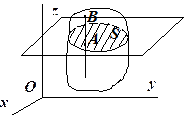
| 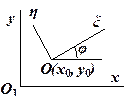
|
| рис. 1.21 | рис. 1.22 |
Зробимо перетин тіла площиною, паралельною основній. Розглянемо рух прямої 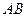 - поступальний. Отже, рух довільної точки
- поступальний. Отже, рух довільної точки 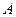 цієї прямої визначає цей поступальний рух. Якщо повторити ці міркування для будь-якої точки плоскої фігури
цієї прямої визначає цей поступальний рух. Якщо повторити ці міркування для будь-якої точки плоскої фігури 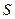 , то можна твердити, що рух тіла повністю визначається рухом цієї фігури
, то можна твердити, що рух тіла повністю визначається рухом цієї фігури 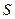 .
.
Складемо рівняння руху плоскої фігури. Виберемо дві системи координат: нерухому 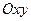 і незмінно зв’язану з плоскою фігурою
і незмінно зв’язану з плоскою фігурою 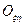 . Положення системи координат
. Положення системи координат 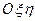 повністю визначає положення плоскої фігури (рис.1.22). Якщо кожному моментові часу
повністю визначає положення плоскої фігури (рис.1.22). Якщо кожному моментові часу 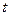 поставити у відповідність значення величин
поставити у відповідність значення величин 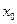 ,
, 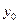 ,
, 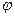 , то дістанемо рівняння, які є законом руху плоскої фігури:
, то дістанемо рівняння, які є законом руху плоскої фігури:
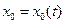 ; (1.55)
; (1.55)
 ; (1.56)
; (1.56)
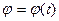 . (1.57)
. (1.57)
Ці рівності – кінематичні рівняння плоскопаралельного руху твердого тіла.
Структура рівнянь показує, що рух плоскої фігури можна розглядати як складний: поступальний разом з полюсом 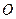 (рівняння (1.55), (1.56)) і обертальний навколо полюса
(рівняння (1.55), (1.56)) і обертальний навколо полюса 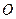 (рівняння (1.57)). Якщо перенести полюс із точки
(рівняння (1.57)). Якщо перенести полюс із точки 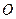 в іншу точку, рівняння (1.57) не зміниться, зміняться лише рівняння (1.55) і (1.56). З цих міркувань можна зробити висновок: при плоскопаралельному русі твердого тіла характеристики обертального руху ( кут повороту
в іншу точку, рівняння (1.57) не зміниться, зміняться лише рівняння (1.55) і (1.56). З цих міркувань можна зробити висновок: при плоскопаралельному русі твердого тіла характеристики обертального руху ( кут повороту 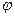 , кутова швидкість
, кутова швидкість 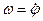 , кутове прискорення
, кутове прискорення 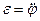 ) не залежать від вибору полюса.
) не залежать від вибору полюса.
Розглядаючи плоскопаралельний рух як окремий випадок руху вільного твердого тіла, можна зобразити 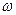 і
і  у вигляді векторів, перпендикулярних до площини руху тіла.
у вигляді векторів, перпендикулярних до площини руху тіла.
Рівняння руху довільної точки 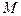 тіла знайдемо, скориставшись формулами перетворення координат:
тіла знайдемо, скориставшись формулами перетворення координат:
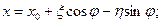
 .(1.58)
.(1.58)
Дата добавления: 2020-08-31; просмотров: 1049;











