Простір і час за Ньютоном. Закони Ньютона

За Ньютоном, простір, в якому здійснюється механічний рух, нерухомий і його властивості не пов’язані із рухом тіла. Властивості простору описуються системою аксіом і теорем геометрії Евкліда.

Висловлюючи твердження про нерухомість простору, Ньютон вважав, що існує абсолютно нерухома, так звана геліоцентрична система координат, початок якої знаходиться у центрі Сонця, а три осі направлені до трьох “нерухомих“ зірок.

Характерною ознакою означення простору за Ньютоном є відірваність властивостей простору від матерії. Ньютон стверджував, що час по своїй суті тече не зупиняючись, рівномірно і однаково в усіх частинах всесвіту. Зміна часу не пов’язана із рухом тіла.

Незважаючи на неточність просторово-часових уявлень, закони Ньютона, що узагальнюють великий дослідний матеріал і спостереження за різними явищами природи, виявилися настільки точні, що і в теперішній час вони є основою розв'язання більшості технічних задач. Відхилення від законів Ньютона трапляються, якщо тіла рухаються поблизу великих скупчень матерії, наприклад, поблизу Сонця. В умовах Землі основою для розрахунків є закони Ньютона. У якості нерухомої системи координат приймають систему, пов’язану із Землею.

Системи координат, у яких справджуються закони Ньютона, називаються інерціальними. Інерціальними (галілеєвськими) є системи координат, що рухаються поступально, прямолінійно і рівномірно відносно "нерухомих" зірок.

Сформулюємо закони Ньютона.

Перший закон Ньютона (закон інерції).

Ізольована матеріальна точка зберігає стан рівномірного і прямолінійного руху або знаходиться у стані спокою відносно системи координат, яка рухається поступово, рівномірно і прямолінійно доти, доки вплив інших тіл не виведе її з цього стану.

Ізольованою називається матеріальна точка, взаємодією якої з навколишніми тілами можна знехтувати. Властивість ізольованої матеріальної точки зберігати стан рівномірного прямолінійного руху називається інертністю.

Закон інерції містить два основних твердження .

1. Згідно із першим законом Ньютона, матеріальній точці притаманний стан руху. Отже, у законі інерції вперше стверджується, що рух є основною первісною властивістю речовини. До XVII ст. у науці домінували погляди Аристотеля, згідно з якими основною властивістю речовини приймався стан спокою. Тому твердження Ньютона створило переворот у науці, а подальший технічний прогрес підтвердив його правильність.

2. З нього випливає, що спонтанна зміна руху матеріальної точки неможлива, а здійснюється лише внаслідок її взаємодії з іншими тілами.

У першому законі Ньютона розглядається прямолінійний рух точки за інерцією. Такий рух можна спостерігати або у лабораторних умовах, або уявивши частинку метеорного пилу, що рухається у міжгалактичному просторі.

Більшість матеріальних точок і тіл, за рухами яких спостерігають на Землі, не рухаються рівномірно і прямолінійно. Це трапляється тому, що на них не діють механічні сили .

Механічна сила – це міра механічного впливу на матеріальну точку з боку оточуючих її точок або тіл. Механічна сила характеризується своєю величиною і напрямом у просторі. Тому її можна представити у вигляді вектора (рис.2.1).

Механічна сила – причина, відхиляюча рух точки від рівномірного і прямолінійного.

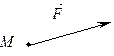
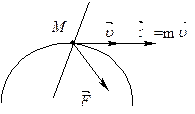
рис.2.1	рис.2.2

Для вимірювання сили Декартом у XVII ст. було введено поняття про кількість руху. Кількістю руху точки називається вектор 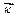, який дорівнює добутку маси точки m на її швидкість 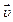(рис.2.2) Вектор 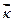колінеарний до вектора швидкості .

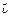Другий закон Ньютона (основний закон динаміки).

Швидкість зміни кількості руху точки дорівнює вектору сили, прикладеної до точки

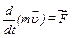. (2.1)

Нижче розглядаються задачі механіки, в яких маса точки є постійною, тому

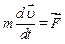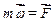, або (2.2)

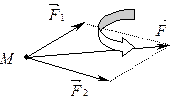
рис.2.3

Рівність (2.2) дозволяє легше сформулювати другий закон Ньютона: добуток маси точки на її прискорення рівний вектору сили, що діє на точку.

Це формулювання другого закону Ньютона буде прийнято у даному курсі.

Масою матеріальної точки називається фізична величина, яка є мірою її інертних і гравітаційних властивостей.

До матеріальної точки може прикладатись декілька сил. У спеціальній примітці до другого закону Ньютон сформулював аксіому 1 (про паралелограм сил): якщо на точку діють дві сили під кутом одна до одної, то точка буде рухатись так, як рухалась би під дією одної сили, рівній діагоналі паралелограма, побудованого на цих силах як на сторонах (рис.2.3). Сила 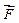називається рівнодійною і дорівнює

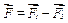. (2.3)

Аксіома про паралелограм сил підтверджує векторну природу сил. Якщо до матеріальної точки M прикладені деякі сили, їх можна додавати по дві послідовно. Нехай, до точки М прикладені три сили 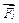, , 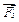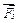(рис.2.4а). Щоб знайти рівнодійну цих сил, додамо спочатку сили 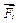і 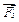, знайдемо їх рівнодійну 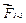. Потім, додавши силу 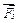, знайдемо рівнодійну

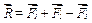(а)

Правило паралелограма можна замінити правилом многокутника сил. Дійсно, щоб знайти рівнодійну, потрібно знайти точку А (рис.2.4б) .Для цього з точки 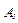, кінця вектора 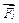, потрібно провести вектор, геометрично рівний вектору 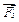. В точці 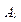, кінця вектора 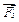, будують вектор, геометрично рівний вектору .

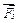З’єднавши початок першої сили (точку М) з кінцем останньої сили (точкою А), отримаємо рівнодійну всіх трьох сил 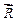як сторону, що замикає многокутник сил (рис.2.4б).

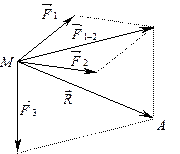
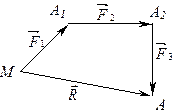
а)	б)
рис.2.4

Розглянемо часткову, але дуже важливу задачу про рівновагу матеріальної точки. Точка, яка знаходиться під дією системи сил і при цьому із прискоренням, рівним нулю, знаходиться у рівновазі.

Рівнодійна системи сил може бути представлена згідно із другим законом Ньютона

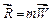. (b)

Якщо при рівновазі точки її прискорення рівне нулю, то умовою рівноваги точки являється рівність нулю рівнодійної

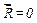. (2.4)

Механічна умова рівноваги системи сил , прикладених до точки.

Матеріальна точка знаходиться у рівновазі, якщо рівнодійна сил, прикладених до точки, рівна нулю.

Графічна умова рівноваги системи сил, прикладених до точки.

Матеріальна точка, на яку діє система сил, знаходиться у рівновазі, якщо многокутник сил, що діють на точку, є замкненим.

Для того щоб закінчити розглядати закони Ньютона, наведемо формулювання його третього закону, який зветься законом дії і протидії. Дією називається сила, що діє на точку, протидією – та сила, з якою точка діє на джерело першої сили. Дія і протидія завжди прикладені до різних точок або тіл.

Третій закон Ньютона (закон рівності дії і протидії).

Дія завжди рівна і прямо протилежна протидії.

Третій закон справедливий у будь-якій системі координат, бо він не містить кінематичних характеристик руху матеріальних об'єктів і дає змогу відрізнити реальні сили, прикладені до точок, від фіктивних, які можуть з'явитися при математичному розв'язанні задач механіки.

У перших двох законах Ньютона розглядається одна матеріальна точка , а у третьому законі - питання про взаємодію двох точок. Механічні взаємодії двох точок не зрівноважують один одне, бо вони прикладені до різних точок.

Для розв'язання задач статики необхідно ознайомитися з деякими аксіомами і теоремами механіки.

рис.2.5

Розглянемо абсолютно тверде тіло, до якого прикладені дві сили, рівні за величиною і направлені по одній прямій в протилежні напрямки (рис.2.5). Пряма, по якій направлена сила, називається її лінією дії.