Розподіл прискорень при плоскопаралельному русі твердого тіла

Прискорення довільної точки тіла при плоскопаралельному русі дорівнює векторній сумі прискорення полюса і прискорення обертального руху навколо полюса.

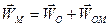(1.64)

Для визначення прискорення довільної точки тіла при плоскопаралельному русі скористаємося виразом (1.51):

.

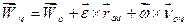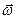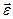Як було згадано раніше, вектори і перпендикулярні до площини руху фігури, тому на підставі властивостей подвійного векторного добутку перепишемо третій доданок у правій частині (1.64):

,

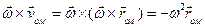Отже

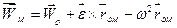, (1.65)

де 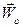- прискорення полюса;

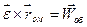- обертальне прискорення

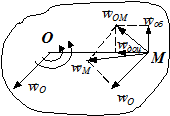
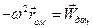- доцентрове прискорення (рис. 1.31).

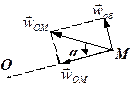
рис.1.31	рис.1.32

Векторна сума обертального прискорення і доцентрового прискорення є прискорення обертального руху плоскої фігури навколо полюса:

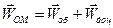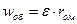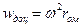; ; (1.66)

Підставивши отримані рівності в (1.51) отримаємо (1.64).

З'ясуємо деякі властивості прискорення обертального руху плоскої фігури навколо полюса. Розглянемо кут a між вектором 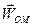і вектором - 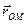. цей кут завжди гострий, бо в противному разі доцентрове прискорення було б напрямлене від полюса, що неможливо. Величину цього кута знайдемо з формули

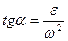(1.67)

З формули (1.67) видно, що кут a не залежить від вибору полюса. Цей кут підліковується від 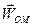до МО (рис. 1.32) у напрямі обертання плоскої фігури, якщо 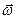і 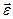мають один напрям, і в протилежному напрямі, якщо напрями 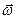і 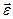- різні.

Нарешті, модуль вектора

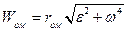(1.68)