Рух вільного твердого тіла. Розподіл лінійних швидкостей і прискорень у вільному твердому тілі
Основна ознака абсолютно твердого тіла – незмінність відстаней між довільними точками такого тіла. Звідси випливає властивість збереження кута між двома довільними прямими, проведеними в абсолютно твердому тілі. Як буде показано далі, цих властивостей досить для визначення основного закону розподілу швидкостей і прискорень у вільному твердому тілі.
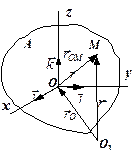
|
| рис.1.17 |
Розглянемо точку 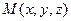 вільного твердого тіла довільної форми (рис.1.17).З тілом А незмінно зв’язана система координат
вільного твердого тіла довільної форми (рис.1.17).З тілом А незмінно зв’язана система координат 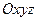 . Точка
. Точка 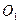 нерухома. Точку
нерухома. Точку 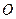 назвемо полюсом. З рис.1.17 видно, що радіус-вектор
назвемо полюсом. З рис.1.17 видно, що радіус-вектор 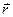 точки
точки 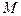 :
:
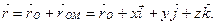 (1.48)
(1.48)
На підставі (1.48) знайдемо швидкість точки М:
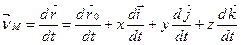 (1.49)
(1.49)
Необхідно знайти похідні 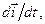
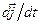 і
і 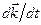 . Для цього скористаємося згаданими властивостями абсолютно твердого тіла. Розглянемо дві системи рівностей
. Для цього скористаємося згаданими властивостями абсолютно твердого тіла. Розглянемо дві системи рівностей
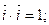
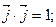
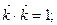 (а)
(а)
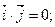
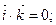
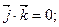 (в)
(в)
Ці рівняння означають збереження довжин ортів 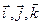 і кутів між ними. Диференціюючи рівності (а) за часом, дістанемо
і кутів між ними. Диференціюючи рівності (а) за часом, дістанемо
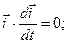
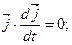
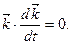 (с)
(с)
Рівності (с) – умови ортогональності векторів відповідно 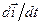 ,
, 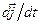 і
і 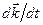 та
та 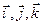 . Тому
. Тому
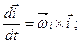
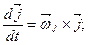
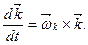 (d)
(d)
Тут 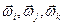 - довільні вектори .
- довільні вектори .
З рівностей (в), після диференціювання їх за часом, дістанемо
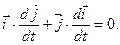 (е)
(е)
Підставляючи (d) в (е) , маємо
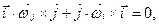 (g)
(g)
звідки на підставі властивостей змішаного добутку векторів
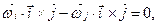 (h)
(h)
або
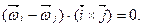 (і)
(і)
Вектор 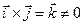 . У загальному випадку руху вільного твердого тіла вектор
. У загальному випадку руху вільного твердого тіла вектор 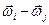 не буде перпендикулярним до орту
не буде перпендикулярним до орту 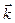 . Отже, рівність (і) виконується, якщо
. Отже, рівність (і) виконується, якщо 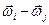 =0, тобто
=0, тобто 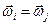 .
.
Аналогічно 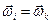 ,
, 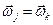 .
.
Отже
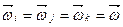 . (j)
. (j)
а рівності (d) мають вигляд:
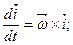
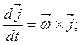
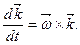 (k)
(k)
Рівність (1.49), що визначає швидкість точки М на підставі (k) набуває вигляду
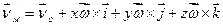 ,
,
або
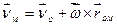 . (1.50)
. (1.50)
Рівність (1.50) визначає закон розподілу швидкостей у вільному твердому тілі. Диференціюючи (1.50) за часом дістанемо закон розподілу прискорень:
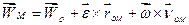 . (1.51)
. (1.51)
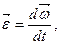
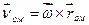 .
.
У виразах (1.50) і (1.51) фізичний зміст векторів 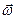 і
і 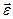 не визначено. Його можна визначити, розглядаючи окремі випадки руху тіла.
не визначено. Його можна визначити, розглядаючи окремі випадки руху тіла.
Наприклад, якщо вісь обертання нерухома і полюс знаходиться на цій осі, то 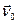 =0 і
=0 і 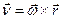 , де
, де 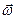 - вектор кутової швидкості, напрямлений вздовж осі.
- вектор кутової швидкості, напрямлений вздовж осі.
На підставі (1.50) і (1.51) можна зробити висновок:
Рух вільного твердого тіла можна розкласти на два рухи: поступальний, що визначається рухом довільної фіксованої точки тіла, яку називають полюсом, і обертальний рух навколо осі, що проходить через полюс. Цю вісь називають миттєвою віссю обертання, а 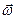 - миттєвою кутовою швидкістю.
- миттєвою кутовою швидкістю.
З рівності (1.48), як наслідок, випливає важлива теорема.
Теорема. Проекції швидкостей двох точок тіла на пряму, що поєднує ці точки, рівні між собою.
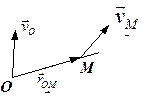
|
| Рис. 1.18 |
Розглянемо точки 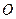 і
і 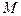 (рис.1.18). Пряма, що їх поєднує це радіус-вектор
(рис.1.18). Пряма, що їх поєднує це радіус-вектор 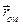 . Орт
. Орт 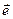 вектора
вектора 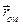 дорівнює відношенню
дорівнює відношенню 
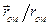 . Помножимо обидві сторони (1.50) скалярно на
. Помножимо обидві сторони (1.50) скалярно на 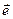 , тобто знайдемо проекцію цієї рівності на
, тобто знайдемо проекцію цієї рівності на 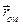 . Другий доданок у правій частині (1.50) перпендикулярний до орта
. Другий доданок у правій частині (1.50) перпендикулярний до орта 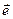 . Тому
. Тому
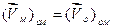 . (1.52)
. (1.52)
Приклади
1. Розглянемо рівнозмінний обертальний рух тіла навколо нерухомої осі. У цьому разі кутове прискорення тіла – величина стала ( 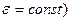 .
.
Згідно з (1.39) 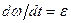 , або
, або 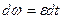 , звідки
, звідки
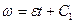 . (а)
. (а)
Користуючись (1.38), маємо
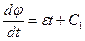 . (в)
. (в)
інтегруючи (в), дістаємо
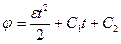 , (с)
, (с)
де 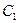 і
і 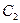 - сталі інтегрування, що знаходяться з початкових умов.
- сталі інтегрування, що знаходяться з початкових умов.
Якщо
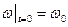 ,
, 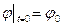 (d)
(d)
то з (в) і (с) дістанемо
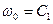 ,
, 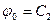 . (е)
. (е)
Підставляючи (е) в (а) і (в), дістаємо закон рівнозмінного обертального руху тіла навколо нерухомої осі:
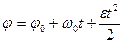 . (1.53)
. (1.53)
і закон зміни кутової швидкості в цьому русі:
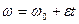 . (1.54)
. (1.54)

|
| рис. 1.19 |
1. Два шківи I і II з’єднано нескінченним пасом (рис.1.19). Радіуси шківів відповідно 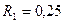 і
і 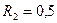 м. Внутрішній радіус шківа II
м. Внутрішній радіус шківа II 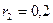 м. Знайти швидкість
м. Знайти швидкість 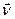 точок паса і кутові швидкості обох шківів, якщо рівняння руху тягаря III
точок паса і кутові швидкості обох шківів, якщо рівняння руху тягаря III 
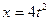 (
(  - в метрах,
- в метрах, 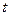 - в секундах).
- в секундах).
Припускаючи, що рух каната відбувається без ковзання, дістаємо, що швидкість точки стикання 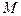 каната зі шківом II дорівнює швидкості тягаря III.
каната зі шківом II дорівнює швидкості тягаря III.
З рівняння руху тягаря ця швидкість 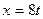
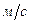 .
.
Отже, кутова швидкість шківа II
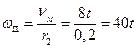
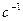 .
.
Оскільки пас рухається без ковзання, то точки ободів шківів мають однакову швидкість 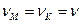 , і
, і
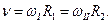
Звідси
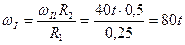
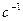 .
.
3. Тіло обертається навколо нерухомої осі згідно з законом 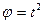 . Визначити швидкість точки тіла на відстані
. Визначити швидкість точки тіла на відстані 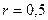 м від осі обертання в момент, коли
м від осі обертання в момент, коли 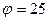 рад.
рад.
Відповідь: 5 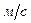 .
.
4. Закон обертального руху тіла 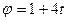 . Визначити прискорення точки тіла на відстані
. Визначити прискорення точки тіла на відстані 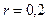 м від осі обертання.
м від осі обертання.
5. Кутова швидкість колеса I змінюється за законом 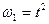 . Визначити прискорення тягаря 3 в момент часу
. Визначити прискорення тягаря 3 в момент часу 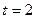 с. Якщо радіуси
с. Якщо радіуси 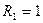 м,
м, 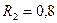 м і
м і 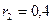 м (рис.1.20).
м (рис.1.20).
Відповідь: 2 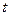
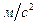 .
.
Дата добавления: 2020-08-31; просмотров: 845;











