Миттєвий центр прискорень

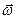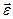Із закону розподілу прискорень при плоскопаралельному русі (1.64) можно зробити висновок, що в тих випадках, коли і одночасно не дорівнюють нулеві, можна знайти таку точку плоскої фігури, вектор прискорення якої в даний момент часу дорівнює нулеві. Ця точка називається миттєвим центром прискорення (МЦП). Якщо полюсом обрати миттьовий центр прискорень, то прискорення кожної точки плоскої фігури можна розглядати як прискорення обертального руху навколо миттьового центру прискорень.

Вектор прискорення 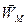довільної точки М утворює визначений за (1.67) кут a з прямою, що з'єднує точку з миттєвим центром прискорень.

Розглянемо два випадки побудови миттєвого центра прискорень.

1. Нехай відоме прискорення 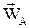точки А (рис.1.33), а також 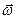і 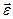. За (1.67) обчислимо кут a і, згідно з напрямом 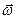і 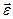, через точку А проведемо пряму АQ, що утворює з вектором 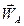кут a. На цій прямій лежить миттьовий центр прискорень, якщо він існує. Щоб знайти його положення на прямій AQ, обчислимо за (1.68) відстань QA від полюса А до МЦП. Відкладаючи від А обчислений відрізок QA, знаходимо миттьовий центр прискорень.

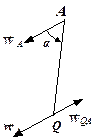
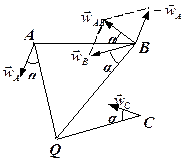
рис.1.33	рис.1.34

2. Припустимо, що відомі прискорення 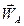і 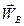двох точок А та В плоскої фігури (рис.1.34). Щоб знайти миттєвий центр прискорень Q, визначимо кут a, який, як було зазначено, не залежить від вибору полюсу. Візьмемо точку А за полюс. На підставі (1.64)

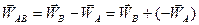
Побудувавши 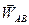(рис.1.34) визначимо кут a між 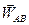і вектором 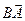. Проведемо з точок А та В прямі AQ і BQ, що утворюють кути a з векторами 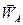і 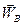. Точка Q перетину цих прямих – миттєвий центр прискорень.

Знаючи положення миттєвого центра прискорень та прискорення однієї точки плоскої фігури, можна побудувати напрями і знайти величини прискорень довільних її точок. Наприклад, прискорення точки С знаходимо, з'єднавши точку С з точкою Q і відкладаючи від цього відрізка кут a у напрямі, оберненому до напряму найкоротшого переходу від 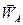до АQ. скориставшись виразом (1.68), обчислимо модуль вектора .

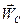Зауважимо що вираз (1.68) дає змогу встановити зв'язок між прискореннями всіх точок плоскої фігури:

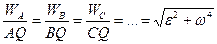. (1.69)

Отже, побудова миттєвого центра прискорень дає змогу повністю вирішити питання про розподіл прискорень при плоскопаралельному русі твердого тіла в певний момент часу.

Приклади

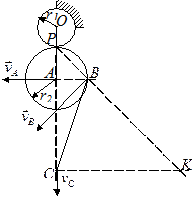
Рис.1.36

1. Розглянемо приклад застосування викладених вище способів визначення розподілу швидкостей у плоскій фігурі.

Механізм, зображений на рис. 1.36, складається з кривошипа ОА=30 см, який обертається навколо осі О з кутовою швидкістю w₀=0,5 рад/с. Зубчасте колесо радіусом r₂=20 cм котиться без ковзання по поверхні нерухомого колеса радіусом 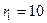см і приводить до руху з’єднаний з ним шарнірно шатун 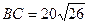см. Визначити кутову швидкість шатуна і швидкості точок В і С в момент, коли радіус АВ перпендикулярний до кривошипа АО.

Розв’язання. З умови видно, що кутову швидкість шатуна можна знайти, якщо відомі швидкості його точок. Точка В спільна для шатуна і рухомого колеса. Тому необхідно розглянути спочатку розподіл швидкостей у рухомому колесі. Точка Р зчеплення рухомого і нерухомого коліс є миттєвий центр швидкостей рухомого колеса. Отже,

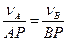
Швидкість точки А легко знайти, розглядаючи обертальний рух кривошипа ОА

.

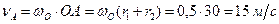Таким чином,

.

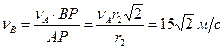Цей самий результат можна дістати, якщо скористатися теоремою про проекції швидкостей двох точок тіла на пряму, що з’єднує ці точки.

Маємо

.

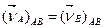Для визначення швидкості точки С і кутової швидкості шатуна побудуємо миттєвий центр швидкостей шатуна ВС. Він знаходиться в точці К перетину прямих ВК і СК , перпендикулярних до векторів швидкостей точок В і С. На підставі (1.63)

.

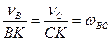Звідси

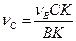
Елементарні геометричні розрахунки дають змогу визначити: СК=120 см, ВК=100 см. Тоді

.

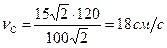
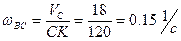2. Розглянемо застосування теореми про розподіл прискорень у тілі при плоскопаралельному русі.

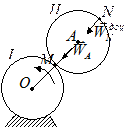
рис.1.36.1

Механізм, зображений на рис.1.36.2, називають епіциклічним. Кривошип ОА обертається зі сталою кутовою швидкістю навколо нерухомої осі О і приводить до руху колесо II, що котиться без ковзання по поверхні колеса I. Радіуси коліс однакові. Знайти прискорення точки 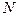колеса II.

Розв’язання. Згідно з (1.68) прискорення довільної точки плоскої фігури складається з прискорення полюса і прискорення обертального руху точки навколо полюса. Полюс слід вибирати в точці, прискорення якої відоме, або його легко визначити з умови задачі. Такою точкою є точка А. Прискорення точки А дорівнює тільки нормальному прискоренню 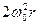і напрямлене від точки А до центра обертання кривошипа ОА.

.

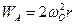Щоб знайти прискорення 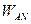, згадаємо, що

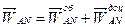
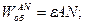
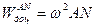
Тут 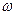і і 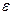- миттєва кутова швидкість і миттєве кутове прискорення, які треба визначити

З умови кочення без ковзання випливає, що швидкість точки М колеса II дорівнює нулеві, тобто точка М є миттєвий центр швидкостей. Тоді миттєва кутова швидкість

.

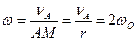
і миттєве кутове прискорення

.

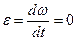Отже,

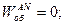
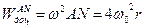
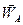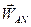Таким чином, прискорення точки N складається з двох векторів і , напрямлених уздовж спільної прямої в одну сторону.

Додаючи їх, маємо

.

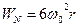рис.1.37

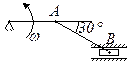
рис.1.38

рис.1.39

Вектор 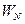напрямлений уздовж прямої NO від точки N до точки O.

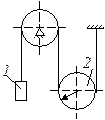
3. Швидкість тягаря 1 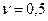м/c. Визначити кутову швидкість рухомого блока 2, якщо його радіус 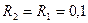м (рис.1.37).

Відповідь: 2,5 1/с.

4. Визначити кутову швидкість шатуна АВ механізму, зображеного на рис.1.38, якщо швидкість точки А 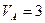м/c, а довжина шатуна АВ=3 м.

Відповідь: 1,15 1/с.

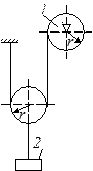
5. Барабан 1 обертається за законом 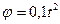. Визначити прискорення тягаря 2, якщо радіус 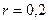м (рис.1.39).

Відповідь: 0,02 м/c.

Розділ 2. Кінетика

Кінетика є частиною теоретичної механіки, що вивчає найбільш загальні властивості механічних рухів і одночасно геометричні властивості рухів і властивості фізичних факторів , які змінюють ці рухи.

В основі кінетики лежать просторово-часові уявлення класичної механіки, закони Ньютона і система аксіом механіки.

Кінетика включає в себе два підрозділи: динаміку і статику.

Динаміка

Динаміка - це розділ теоретичної механіки, що вивчає механічний рух матеріальної точки, системи матеріальних точок і абсолютно твердого тіла з урахуванням сил, що діють на ці рухомі об'єкти.

У динаміці синтезуються й узагальнюються положення статики і кінематики, а також встановлюються найбільш загальні закони механічного руху. При цьому враховується взаємодія між тілами, мірою якої є сила.

Сила - це міра взаємодії між тілами, яка має напрямок, величину і точку прикладання.

Динаміка ставить перед собою дві основні задачі. Перша (пряма задача динаміки) полягає в тому, що за заданими механічним рухом і масою тіла визначають сили, під дією яких цей рух здійснюється. Друга (обернена задача динаміки) полягає у тому, що за даними силами, прикладеними до тіла, його масою і початковими умовами визначають рух, який вони спричиняють.