Обертальний рух твердого тіла навколо нерухомої осі

Обертальним рухом тіла навколо нерухомої осі називають рух твердого тіла, при якому певна пряма (вісь обертання), що проходить через які-небудь дві точки під час руху тіла залишається нерухомою.

Визначимо закон обертального руху тіла навколо осі. Нехай вісь 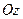, рис.(1.12) є нерухома вісь,навколо якої обертається тіло. Проведемо через вісь 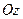у деякий початковий момент часу 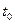площину .

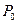Через деякий проміжок часу ця площина займе положення 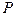, створивши двогранний кут зі своїм початковим положенням. Цей двогранний кут називається кутом повороту і виміряється лінійним кутом .

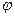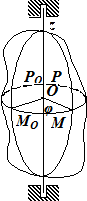
Рис. 1.12

Вважатимемо кут повороту 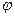додатним, якщо з боку додатного напряму осі 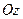цей поворот видно проти ходу годинникової стрілки.

Кожному моментові часу 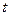відповідає повне значення кута повороту 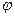. Отже, кут повороту є функція часу:

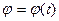(1.37)

Це рівняння називається кінематичним рівнянням обертального руху тіла навколо нерухомої осі.

З кутом повороту 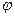пов’язані дві основні кінематичні величини, що характеризують обертальний рух твердого тіла: кутова швидкість і кутове прискорення.

Кутовою швидкістю тіла називають фізичну величину, що характеризує бистроту зміни кута повороту тіла 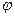у часі.

На підставі попередніх міркувань

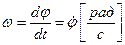. (1.38)

Отже, кутова швидкість дорівнює першій похідній за часом від кута повороту .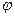

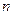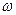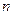У техніці кутову швидкість часто задають числом обертів за хвилину. Зв’язок між та визначається формулою

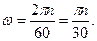
Кутова швидкість визначає також і напрям обертання. Так, якщо 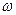>0, то тіло в даний момент обертається в напрямі зростання кута повороту – проти ходу годинникової стрілки, якщо дивитися з боку вибраного додатного напряму осі 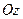, і в протилежному напрямі, якщо 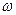< 0.

Кутовим прискоренням називають фізичну величину, що визначає бистроту зміни кутової швидкості в часі. Кутове прискорення можна знайти, якщо продиференціювати за часом кутову швидкість:

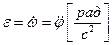(1.39)

Якщо знаки 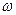і збігаються, то кутова швидкість зростає, обертання прискорене.

Наведені формули визначають 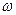і як скалярні величини. Зауважимо, що 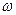і однакові для всіх точок тіла.

Розглянемо розподіл лінійних швидкостей у тілі, що обертається навколо осі. Скористаємося натуральним способом визначення руху точки і розглянемо рух довільної точки 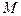тіла. Якщо початкове положення точки 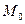відповідає початковому значенню кута повороту 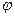, то на підставі (1.31) маємо:

,

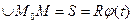де 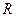- відстань від точки 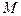до нерухомої осі.

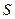- дугова координата, що відповідає куту повороту .

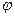Це рівняння є закон руху точки по траєкторії.

Щоб знайти проекцію швидкості точки 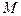на дотичну, продиференціюємо його за часом:

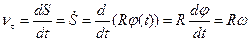, (1.40)

або

.

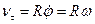Отже, лінійні швидкості залежно від радіуса розподіляються за лінійним законом (рис.1.13).

Щоб знайти розподіл лінійних прискорень, скористаємось формулами (1.30) і (1.40).

Дістанемо

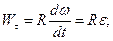
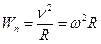(1.41)

Модуль прискорення знайдемо за формулою:

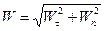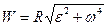; . (1.43)

Кут 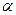між вектором повного прискорення і радіусом обертання (рис.1.14):

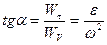. (1.44)

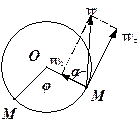
Рис. 1.13	Рис. 1.14

Оскільки 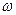і не залежать від положення точки 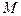, то кут 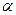однаковий для всіх точок тіла.