Прискорення руху точки
Прискорення є фізична величина, що характеризує бистроту зміни швидкості руху точки за часом.
На підставі цього означення і змісту підрозд. 1.1.3 можна визначити величину і напрям прискорення точки:
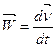 (1.23)
(1.23)
Вектор 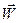 напрямлений по дотичній до годографа вектора швидкості
напрямлений по дотичній до годографа вектора швидкості 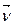 .Знайдемо прискорення точки трьома способами опису її руху.
.Знайдемо прискорення точки трьома способами опису її руху.
Якщо рух точки задано векторним рівнянням 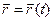 , то швидкість
, то швидкість 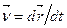 , а на підставі (1.23) прискорення
, а на підставі (1.23) прискорення
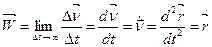 (1.24)
(1.24)
Для визначення прискорення точки координатним способом скористаємось рівностями (1.7) і (1.24):
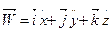 (a)
(a)
Розкладаючи вектор прискорення 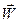 по ортах декартової системи координат
по ортах декартової системи координат
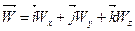 (b)
(b)
і порівнюючи вирази (а) і (b) маємо
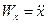 ;
; 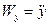 ;
; 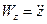 (1.25)
(1.25)
Отже, проекції вектора прискорення на координатні осі дорівнюють першим похідним за часом відповідних проекцій швидкості за часом, або другим похідним відповідних координат рухомої точки за часом.
Модуль вектора 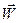 і його напрямні косинуси знаходимо за відповідними формулами аналітичної геометрії:
і його напрямні косинуси знаходимо за відповідними формулами аналітичної геометрії:
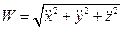 (1.26)
(1.26)
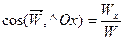 ;
; 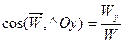 ;
; 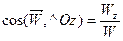 (1.27)
(1.27)
Формули (1.25) – (1.27) визначають вектор прискорення координатним способом.
Натуральні осі та натуральний тригранник. Кінематичні характеристики руху точки тісно пов’язані з геометричними властивостями траєкторії. Як відомо з диференціальної геометрії, у кожній точці кривої є три взаємно перпендикулярні напрямки: дотична, головна нормаль і бінормаль, одиничні вектори (або орти) які позначимо відповідно 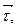
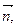
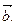
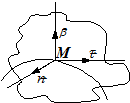
Побудуємо місцевий координатний базис – натуральний тріедр (рис. 1.8). Орти дотичної і головної нормалі створюють стичну площину кривої.
| 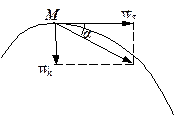
|
| рис. 1.8 | рис. 1.9 |
Проведемо нормаль до цієї площини. Цю нормаль називають бінормаллю, її орт 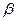 . У площині (
. У площині ( 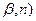 розміщені всі нормалі до кривої, тому орти (
розміщені всі нормалі до кривої, тому орти ( 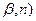 створюють нормальну площину кривої. Орти (
створюють нормальну площину кривої. Орти ( 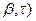 створюють спрямляючу площину кривої. Орти (
створюють спрямляючу площину кривої. Орти ( 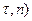 створюють стичну площину.
створюють стичну площину.
Прискорення точки при натуральному способі задання руху визначається за такою теоремою.
Теорема. Повне прискорення точки дорівнює векторній сумі дотичного (тангенціального) та нормального прискорень.
Доведення. Нехай рух точки задано натуральним способом.
Із (1.22) і (1.23) дістанемо
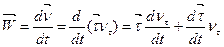 . (с)
. (с)
Перший доданок називається дотичною, або тангенціальною складовою прискорення і позначається 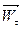 . Отже,
. Отже,
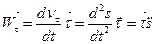
З цього рівняння випливає, що дотичне прискорення характеризує зміну швидкості за величиною і дорівнює першій похідній за часом від проекції швидкості на дотичну або другій похідній від дугової координати за часом.
Зауважимо, що орт 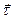 змінює свій напрям зі зміною дугової координати
змінює свій напрям зі зміною дугової координати 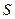 , тобто його можна розглядати як складну функцію часу
, тобто його можна розглядати як складну функцію часу 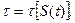 Отже, другий доданок можна подати у вигляді:
Отже, другий доданок можна подати у вигляді:
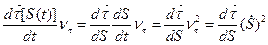 . (d)
. (d)
Візьмемо похідну від 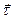 за
за 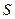 :
:
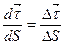 (e)
(e)
Розглянемо тотожність 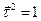 та продиференціюємо її по S.
та продиференціюємо її по S.
Тоді одержимо:
а) 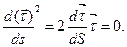 Із цього випливає, що вектори
Із цього випливає, що вектори 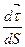 і
і 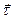 - перпендикулярні (рис.1.10);
- перпендикулярні (рис.1.10);
б) вектор 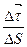 завжди напрямлений у бік угнутості траєкторії.
завжди напрямлений у бік угнутості траєкторії.
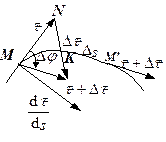
|
| рис. 1.10 |
в) вектор 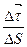 лежить у стичній площині;
лежить у стичній площині;
Вектор 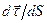 напрямлений, як відомо, по дотичній до годографа вектора
напрямлений, як відомо, по дотичній до годографа вектора 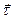 . Оскільки
. Оскільки 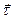 - одиничний вектор, його годограф є крива, розміщена на поверхні сфери одиничного радіуса. Тому вектор
- одиничний вектор, його годограф є крива, розміщена на поверхні сфери одиничного радіуса. Тому вектор 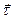 утворює з вектором
утворює з вектором 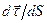 прямий кут (рис.1.10). З’ясуємо, вздовж якої нормалі напрямлений вектор
прямий кут (рис.1.10). З’ясуємо, вздовж якої нормалі напрямлений вектор 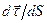 . Для цього розглянемо граничний напрям вектора
. Для цього розглянемо граничний напрям вектора 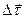 . Щоб його побудувати, проведемо одиничні вектори
. Щоб його побудувати, проведемо одиничні вектори 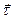 і
і 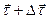 в сусідніх точках
в сусідніх точках 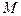 і
і 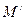 , де
, де 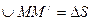 . Побудуємо в точці
. Побудуємо в точці 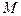 вектор
вектор 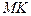 , що дорівнює
, що дорівнює 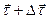 . Тоді
. Тоді 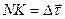 .
.
Якщо 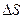 прямує до нуля, точка
прямує до нуля, точка 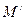 прямує
прямує 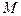 ,
, 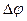 прямує до нуля, то площина трикутника
прямує до нуля, то площина трикутника 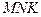 , обертаючись навколо нерухомого вектора
, обертаючись навколо нерухомого вектора 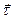 , наближається до певного граничного положення. Це граничне положення площини трикутника
, наближається до певного граничного положення. Це граничне положення площини трикутника 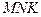 знаходиться в стичній площині кривої в точці
знаходиться в стичній площині кривої в точці 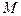 . Отже, нормаль, вздовж якої напрямлений вектор
. Отже, нормаль, вздовж якої напрямлений вектор 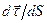 , лежить в стичній площині.
, лежить в стичній площині.
Зауважимо, що всяка плоска крива всіма точками лежить у стичній площині.
З рис. 1.10 видно, що вектор 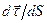 напрямлений у бік угнутості кривої, тобто в бік її центра кривизни траєкторії.
напрямлений у бік угнутості кривої, тобто в бік її центра кривизни траєкторії.
Визначимо модуль вектора 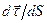 :
:
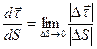 .
.
З рис. 1.10 знаходимо

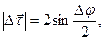
тому
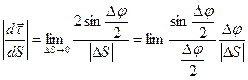
Оскільки
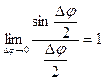 ;
; 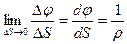
де 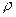 - радіус кривизни кривої , то
- радіус кривизни кривої , то
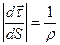 (i)
(i)
Позначимо одиничний орт головної нормалі через 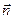 напрямимо його в бік угнутості кривої. Тоді
напрямимо його в бік угнутості кривої. Тоді
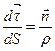 (j)
(j)
На підставі (d) і ( 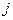 ) вираз (c) набуває вигляду
) вираз (c) набуває вигляду
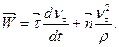 (1.28)
(1.28)
Зауважимо, що 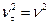 , де
, де 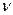 модуль швидкості.
модуль швидкості.
Розкладемо вектор 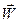 по ортах натурального тріедра:
по ортах натурального тріедра:
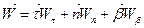 (1.29)
(1.29)
і порівняємо здобутий вираз із формулою (1.28):
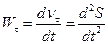 ;
; 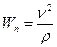 . (1.30)
. (1.30)
Як видно з (1.29), (1.30), проекція вектора прискорення на бінормаль дорівнює нулеві.
Отже, вектор прискорення точки лежить завжди у стичній площині траєкторії точки. Проекцією 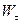 називають дотичним, або тангенціальним прискоренням, проекцію
називають дотичним, або тангенціальним прискоренням, проекцію 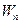 - доцентровим, або нормальним прискоренням.
- доцентровим, або нормальним прискоренням.
Повне прискорення точки є векторна сума дотичного і нормального прискорень (рис.1.9).
Із (1.30) витікає очевидний фізичний зміст складових прискорення: тангенціальне прискорення характеризує зміну швидкості за величиною, нормальне – за напрямом. Дійсно, якщо точка рухається рівномірно ( 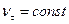 ), то
), то 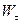 =0. Якщо траєкторія точки – пряма лінія, то
=0. Якщо траєкторія точки – пряма лінія, то 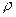 =
= 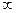 і
і 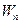 =0.
=0.
Таким чином, модуль прискорення і його напрям знаходяться із виразів:
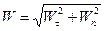 ;
; 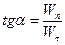 . (1.31)
. (1.31)
Отже, формули (1.28), (1.30), (1.31) визначають вектор прискорення натуральним способом.
Приклади
1. Рівнозмінний рух точки.
Рух точки називається рівнозмінним, якщо її дотичне прискорення стале ( 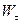 =а). Знайдемо швидкість точки і закон її руху по траєкторії.
=а). Знайдемо швидкість точки і закон її руху по траєкторії.
На підставі (1.30)
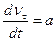 ;
; 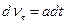
звідки
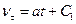 .
.
За формулою (1.21)
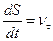 ;
; 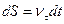 ,
,
звідки після інтегрування маємо
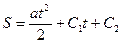 ,
,
де 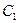 і
і 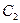 - сталі інтегрування, що знаходяться з початкових умов. У даному випадку початковими умовами є початкова швидкість і початкова дугова координата. Нехай
- сталі інтегрування, що знаходяться з початкових умов. У даному випадку початковими умовами є початкова швидкість і початкова дугова координата. Нехай
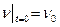 ;
; 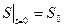
Дістанемо ,
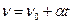 ; (1.32)
; (1.32)
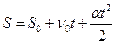 (1.33)
(1.33)
2. Рух точки визначається рівняннями 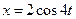 ,
, 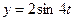 ,
, 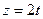 (
( 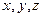 - у метрах,
- у метрах, 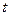 - в секундах ). Визначити радіус кривизни траєкторії точки.
- в секундах ). Визначити радіус кривизни траєкторії точки.
На підставі (1.30) знаходимо 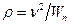 . Отже, треба обчислити
. Отже, треба обчислити 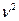 і
і 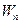 .
.
З рівнянь руху маємо
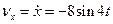 ;
;
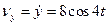 ;
; 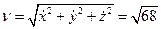
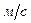 ;
;
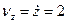 .
.
Швидкість точки – стала величина .
Нормальне прискорення визначимо через повне і тангенціальне за формулами (1.30) і (1.31) :
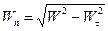 .
.
Повне прискорення
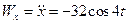 ;
;
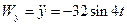 ;
; 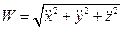 ;
;
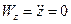 ;
; 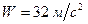
Оскільки 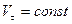 , а
, а 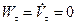 , то
, то 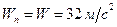 .
.
Знаходимо
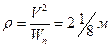
3. Рух точки відбувається за законом 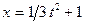 ;
; 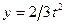 .
.
Визначити швидкість , прискорення точки, радіус кривизни траєкторії і закон руху точки по траєкторії.
Відповідь: 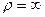
4. В певний момент часу повне прискорення точки дорівнює 2,6 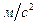 . Точка рухається по кривій з дотичним прискоренням 1,4
. Точка рухається по кривій з дотичним прискоренням 1,4 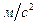 . Знайти для даного моменту часу нормальне прискорення точки.
. Знайти для даного моменту часу нормальне прискорення точки.
Відповідь: 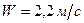 .
.
Дата добавления: 2020-08-31; просмотров: 1485;











