Годограф векторної функції
Введемо поняття про годограф функції 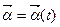 . Це поняття для векторної функції аналогічне поняттю графіка скалярної функції
. Це поняття для векторної функції аналогічне поняттю графіка скалярної функції 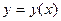 . Якщо
. Якщо 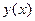 - неперервна функція, то неперервній зміні аргумента
- неперервна функція, то неперервній зміні аргумента  відповідає неперервна зміна функції
відповідає неперервна зміна функції  . Ця зміна визначається графіком (рис.1.4).
. Ця зміна визначається графіком (рис.1.4).
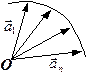
|
| Рис. 1.4 |
Розглянемо векторну функцію 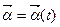 . Надаючи аргументові
. Надаючи аргументові 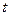 значення
значення 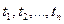 , дістанемо відповідні значення функції
, дістанемо відповідні значення функції 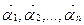 . Проведемо з фіксованої точки О вектори
. Проведемо з фіксованої точки О вектори 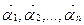 . Якщо аргумент
. Якщо аргумент 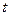 змінюється неперервно, то кінці перенесених векторів
змінюється неперервно, то кінці перенесених векторів 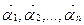 утворюють суцільну криву, що називається годографом векторної функції. Щоб знайти рівняння годографа, досить вибрати довільну ортогональну систему координат
утворюють суцільну криву, що називається годографом векторної функції. Щоб знайти рівняння годографа, досить вибрати довільну ортогональну систему координат 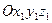 з початком у точці О і знайти проекції вектора
з початком у точці О і знайти проекції вектора 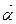 на ці координатні осі.
на ці координатні осі.
Рівняння
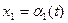 ;
; 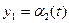 ;
; 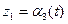 (1.13)
(1.13)
є скалярні рівняння годографа векторної функції 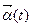 .
.
Розглянемо питання про похідну від функції 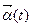 . Похідною векторної функції
. Похідною векторної функції 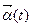 називатимемо змінний вектор, що означається рівністю
називатимемо змінний вектор, що означається рівністю
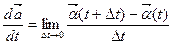 ; (1.14)
; (1.14)
якщо границя в правій частині (1.14) існує.
Доведемо, що похідна 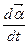 є вектор, напрямлений по дотичній до годографа функції
є вектор, напрямлений по дотичній до годографа функції 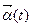 .
.
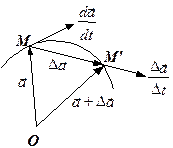
|
| рис. 1.5 |
Розглянемо приріст аргумента 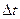 і відповідний йому приріст функції
і відповідний йому приріст функції 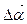 . Певному значенню функції
. Певному значенню функції 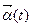 відповідає точка М, її годографа (рис.1.5). Векторові
відповідає точка М, її годографа (рис.1.5). Векторові 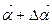 відповідає точка
відповідає точка 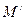 годографа. Відношення
годографа. Відношення 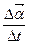 є вектор, напрямлений по січній
є вектор, напрямлений по січній 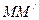 годографа функції
годографа функції 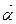 . Якщо
. Якщо 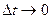 , а точка
, а точка 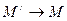 , то січна
, то січна 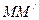 наближається до дотичної в точці М. Отже, вектор
наближається до дотичної в точці М. Отже, вектор 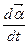 напрямлений по дотичній до годографа функції
напрямлений по дотичній до годографа функції 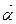 .
.
Як відомо, похідна від скалярної функції визначає напрям дотичної до графіка функції, а її фізичний зміст полягає у визначенні темпу зміни функції залежно від зміни аргументу. Отже, фізичний зміст похідної векторної функції можна вважати аналогічним – похідна векторної функції 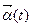 визначає темп зміни вектора
визначає темп зміни вектора 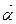 і напрямлена по дотичній до годографа функції
і напрямлена по дотичній до годографа функції 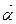 .
.
Дата добавления: 2020-08-31; просмотров: 742;











