Швидкість руху точки

Перейдемо до вивчення основних кінематичних величин, що характеризують рух точки в просторі. Такими величинами є швидкість точки та її прискорення.

Як і в підрозділі 1.1.2. користуватимемося трьома способами визначення руху точки.

Швидкістю точки називають фізичну величину, що характеризує бистроту зміни положення точки в просторі зі зміною часу.

При векторному способі визначення руху точки закон її руху має вигляд 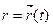. Траєкторія точки – годограф функції 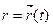. На основі визначення поняття швидкості і фізичного змісту похідної векторної функції скалярного аргументу робимо висновок, що швидкість точки є вектор, який дорівнює першій похідній від радіуса-вектора:

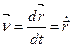(1.15)

Тут і далі диференціюванням за часом позначене крапкою.

Вектор швидкості напрямлений по дотичній до годографа вектора 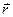, тобто по дотичній до траєкторії точки в той бік, що відповідає зростанню часу t (рис.1.6).

Рівність (1.15) визначає вектор швидкості точки векторним способом математичного опису її руху.

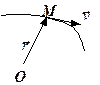
рис. 1.6

Розглянемо визначення швидкості координатним способом. З рівностей (1.7) і (1.15) маємо:

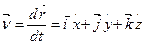(а)

Розкладаючи вектор 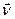по ортах ортогональної системи декартових координат

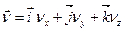(b)

Порівнюючи вирази (а) і (b), маємо

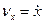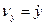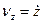; ; . (1.16)

Отже, проекції швидкості на координатні осі дорівнюють першим похідним за часом від відповідних координат точки.

Знаючи проекції вектора швидкості на координатні осі, легко знайти модуль вектора швидкості і його напрямні косинуси:

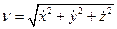; (1.17)

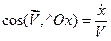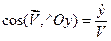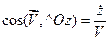; ; . (1.18)

Рівності (1.16) – (1.18) визначають вектор швидкості точки координатним способом математичного опису її руху.

Знайдемо швидкість, припускаючи, що рух точки задано натуральним способом, а отже відомі її траєкторія та закон (рівняння) руху по траєкторії 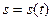. Кожній точці траєкторії відповідає певний радіус-вектор 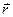, який можна розглядати як складну функцію часу 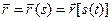, тому формулу (1.15) для швидкості подамо у вигляді

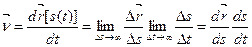(c)

З’ясуємо зміст кожного співмножника в рівності (с):

Розглянемо вектор

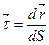(1.19)

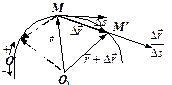
рис. 1.7

На підставі змісту підроз. 1.1.3 твердимо, що цей вектор напрямлений по дотичній до траєкторії у бік додатних дугових координат. Справді, якщо 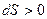, то вектор 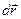напрямлений у бік додатних дугових координат 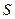(рис.1.7).

У цей самий бік напрямлений і вектор 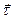. Зі зміною знака 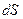змінюється і знак 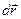. Отже, напрям 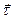залишається попереднім.Модуль вектора 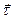дорівнює одиниці:

,

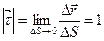оскільки 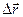є довжина хорди 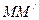(рис.1.7).

На підставі викладеного дістанемо

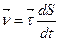(1.20)

Щоб визначити 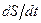, домножимо рівність (1.20) скалярно на орт .

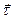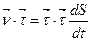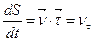; (1.21)

Отже, 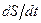є проекція швидкості на дотичну до траєкторії.

Таким чином,

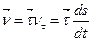(1.22)

Рівності (1.20) – (1.22) визначають вектор швидкості точки натуральним способом математичного опису її руху.