Уравнения движения электропривода

Наиболее удобным методом составления уравнений движе­ния механической части привода являются уравнения Лагранжа второго рода. При этом предполагается, что движение механической части исследуется в системе обобщенных коорди­нат, в качестве которых должны быть приняты независимые пара­метры, определяющие положения механизма. Такими параметра­ми являются углы поворота вращающихся вокруг неподвижных осей дискретных инерционных элементов q_t и их линейные пере­мещения S_i (рис. 2.11).

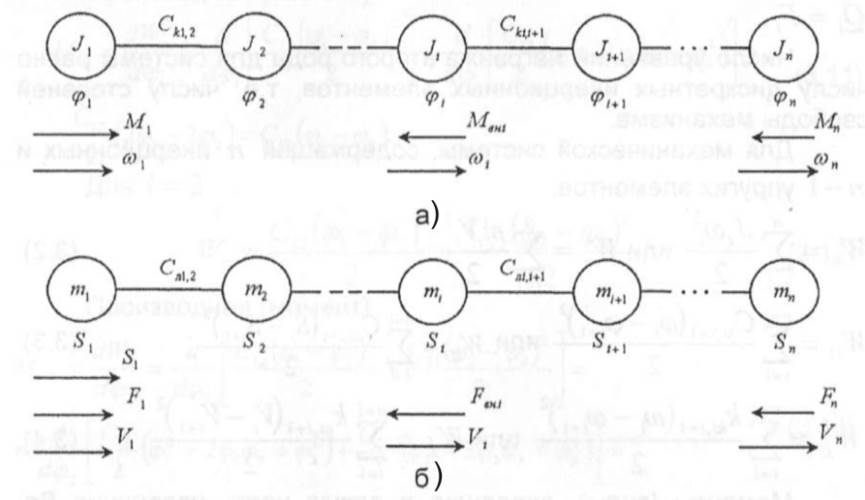Рис. 2.11 Расчетные схемы механической части: а - для вращающихся элементов; б - для поступательно движущихся элементов

Уравнение Лагранжа второго рода

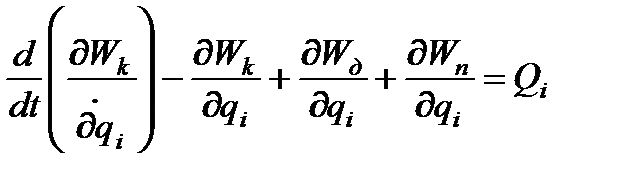, (2.28)

где 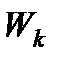- кинетическая энергия системы ;

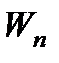- потенциальная энергия системы;

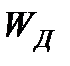–работа сил рассеяния (диссипативная функция Релея);

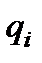- обобщенная координата;

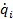- обобщённая скорость;

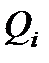- обобщённая внешняя сила, соответствующая обобщённой координате.

При вращательном движении , ;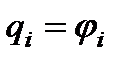

;

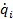
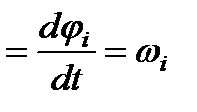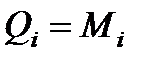при поступательном движении , ,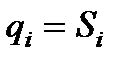

.

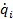
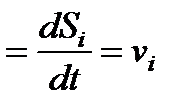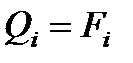Число уравнений Лагранжа второго рода для системы равно числу дискретных инерционных элементов, т.е. числу степеней свободы механизма.

Для механической системы, содержащей n инерционных и n 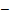1 упругих элементов:

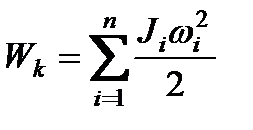или 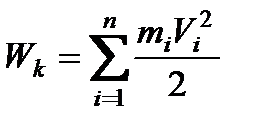; (2.29)

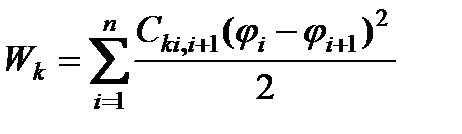или 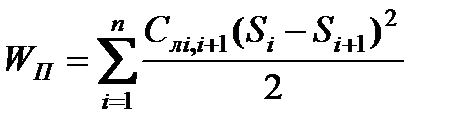; (2.30)

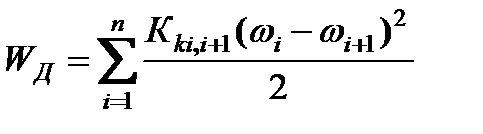или 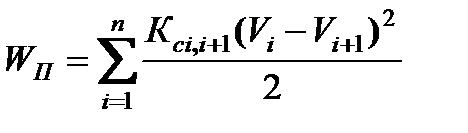. (2.31)

Моменты (силы), входящие в левую часть уравнения Ла­гранжа (2.28) и действующие на 1-й инерционный элемент системы, определяются как

1)инерционные

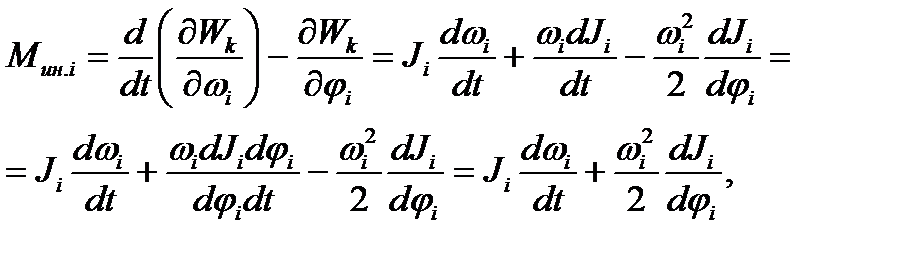(2.32)

где = ;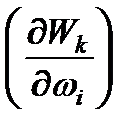

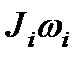2)потенциальные

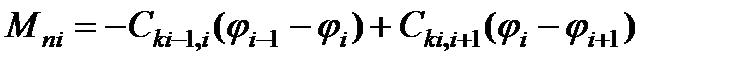; (2.33)

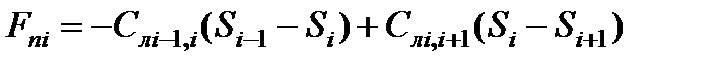; (2.34)

3) диссипативные

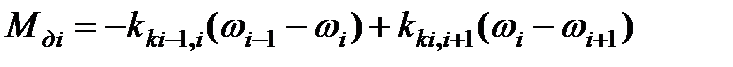; (2.35)

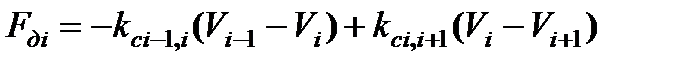. (2.36)

Для =1 (для первой массы)

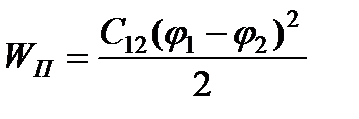. (2.37)

Производная (момент)

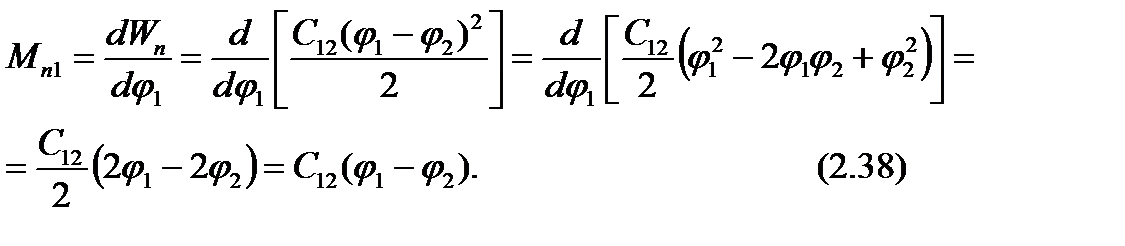
Для 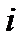=2

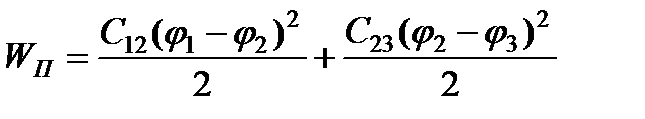. (2.39)

Производная (момент)

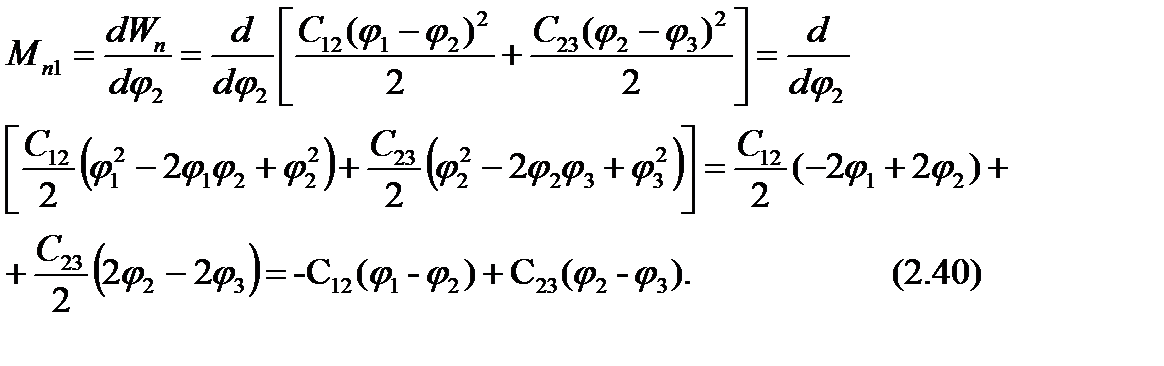
В соответствии с уравнением Лагранжа (2.28) для любого 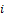- гo звена может быть записано уравнение движения

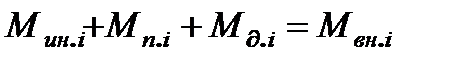; (2.41)

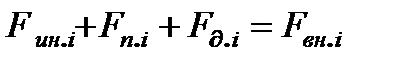, (2.42)

где 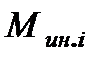, 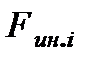- суммарный внешний момент (сила), действующий на 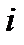-ое звено.

В тех случаях, когда момент инерции (масса) звена не зависит от его положения, 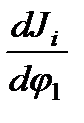=0 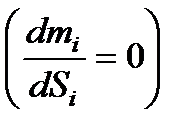, получим

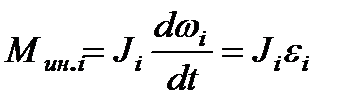; (2.43)

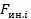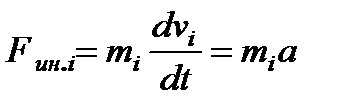= , (2.44)

где 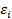, 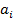– угловое и линейное ускорение.

Диссипативные силы в упругих связях, обусловленные сила­ми вязкого трения, существенно меньше потенциальных сил, в связи с чем при исследовании законов движения электроприводов механизмов в первом приближении их можно не учитывать.

С учетом указанных допущений уравнения движения в слу­чае трехмассовой системы имеют следующий вид

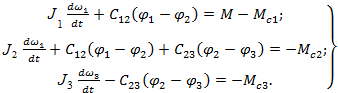(2.45)

Для двухмассовой системы

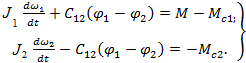(2.46)

С учётом, что момент упругой связи 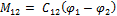, уравнения 2.46 запишутся в следующем виде

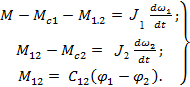
(2.47)

Для одномассовой абсолютно жесткой системы на основа­нии (2.32) при J = var можно записать уравнение движения

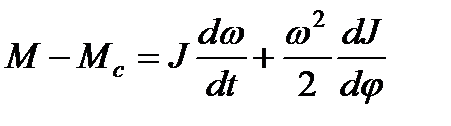, (2.48)

а при 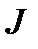= const

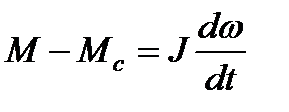. (2.49)