Расчётные схемы механической части электропривода

Кинематические схемы электроприводов дают представле­ние об идеальных связях между движущимися массами конкретной установки ( см. рис. 2.2-2.8), отражают передачу электромагнитной мощности (момента) от двигателя к рабочему органу механизма. Однако они не отражает того, что:

1. Все элементы при нагружении деформируются, т.е. обла­дают конечной жесткостью.

2. В общем случае инерционные массы системы движутся с различными скоростями.

3. В элементах механической части имеются зазоры.

Поэтому для анализа условий движения механической части

привода необходимо с помощью кинематической схемы составить расчетную механическую схему, в которой моменты инерции и мо­менты нагрузки вращающихся элементов, массы и действующие силы поступательно движущихся элементов, зазоры, а также ре­альные жесткости механических связей заменены эквивалентными величинами, приведёнными к одной и той же расчетной скорости. Обычно приведение схемы осуществляется к угловой скорости двигателя, но возможно к любой скорости.

Условием соответствия приведенной расчетной схемы ре­альной механической системе является выполнение закона сохра­нения энергии.

При приведении необходимо обеспечить сохранение потен­циальной и кинетической энергии системы, а также элементарной работы всех действующих в системе сил и моментов на всех воз­можных перемещениях.

Переход к расчетной схеме механической части электропри­вода рассмотрим на примере кинематической схемы электроприво­да, приведённой на рис. 2.9, в движении которой присутствуют N вращающихся элементов и К поступательно движущихся масс.

В рассматриваемой кинематической схеме двигатель Д че­рез соединительную муфту СМ1, ряд зубчатых передач ЗП₁...ЗП_i и соединительную муфту СМ2 приводит во вращение барабан Б, который преобразует вращательное движение в поступательное пере­мещение ряда связанных масс. В данной схеме рабочим органом является грузозахватное устройство, перемещающее груз с мас­сой 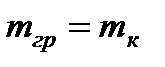. Груз движется со скоростью Vгр и имеет силу тя­жести F = F_K. Каждый вращательно движущийся элемент обладает мо­ментом инерции 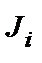и связан с (i +1) -м элементом механической связью, обладающей жесткостью .

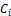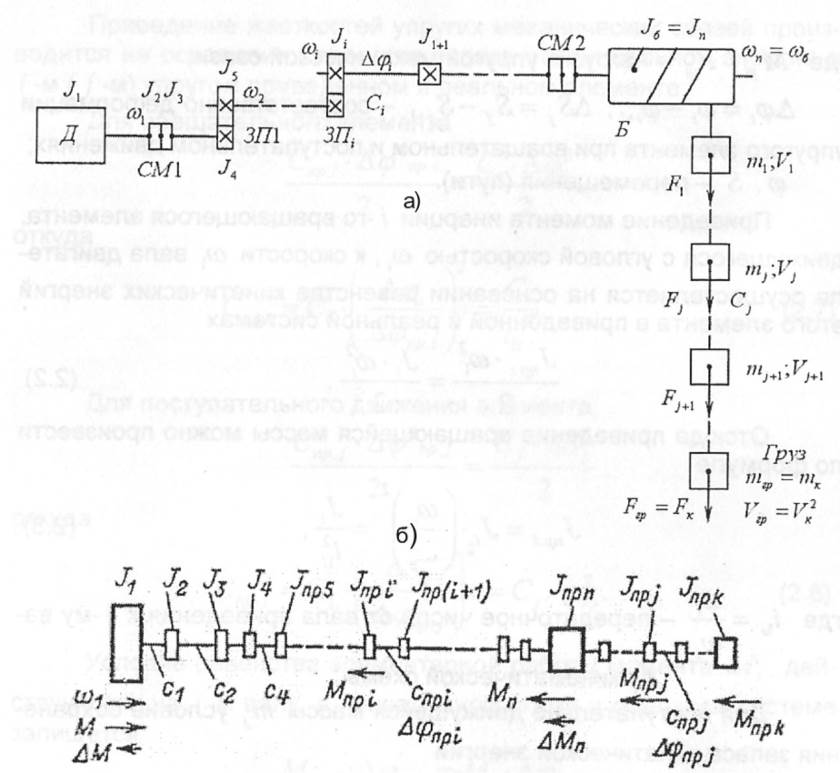. Рис. 2.9. Кинематическая (а) и расчетная (б) схемы механической части электропривода подъёма

Соответственно каждый по­ступательно движущийся элемент имеет массу 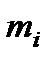и связан с (j+1)-м элементом механической связью с жесткостью 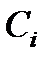. Для механических связей, деформация которых подчиняется закону Гука, их жесткости можно определить по формулам:

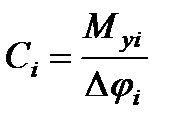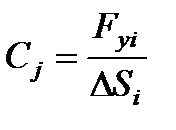, (2.6)

где 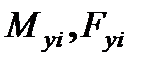– нагрузка упругой механической связ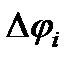и;

и 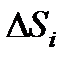- соответственно деформации упругого элемента при вращательном и поступательном движениях;

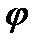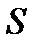, - перемещение (путь).

Приведение момента инерции - го вращающегося элемента, движущегося с угловой скоростью 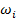, к скорости 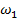вала двигателя осуществляется на основании равенства кинетических энергий этого элемента в приведённой и реальной системах

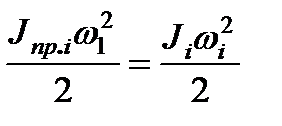. (2.7)

Отсюда приведение вращающейся массы можно произвести по формуле

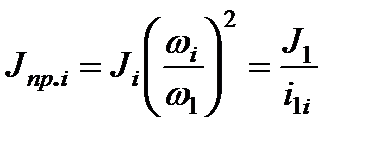, (2.8)

где 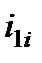– передаточное число от вала приведения к 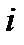-му валу кинематической схемы.

Для поступательно движущейся массы 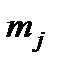условие сохранения запаса кинетической энергии

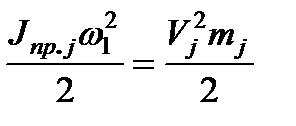; (2.9)

Откуда

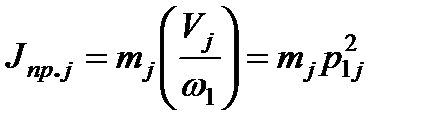
(2.10)

где 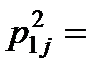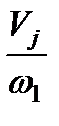– радиус приведения j-го поступательно движущегося элемента к скорости приведения .

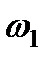Приведение вращательных 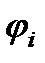и поступательных перемещений к угловой скорости 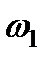осуществляется по формулам

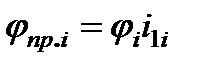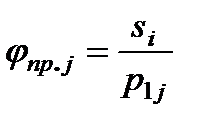; . (2.11)

Приведение жёсткостей упругих механических связей производится на основании равенства запаса потенциальной энергии в -ом (j-ом) упругом приведённом и реальном элементах:

для вращательного элемента

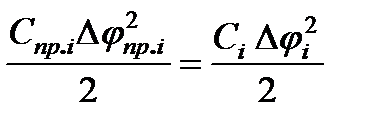, (2.12)

откуда

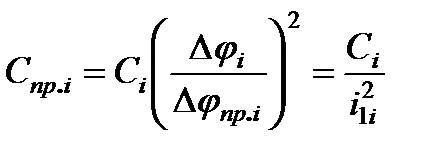, (2.13)

для поступательного движущегося элемента

,

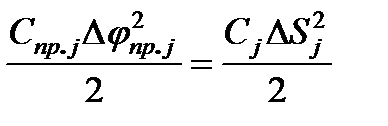откуда

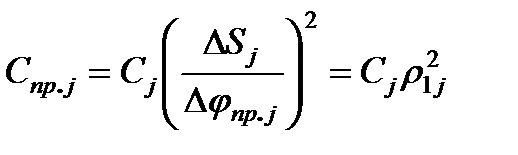. (2.14)

Условие равенства элементарной работы момента 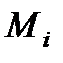, действующего на - ом валу, в приведённой схеме и реальной системе запишется

,

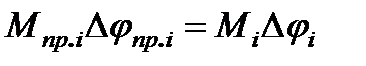откуда

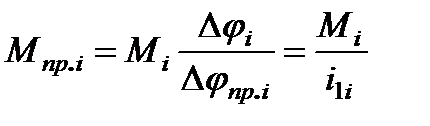. (2.15)

Аналогично для силы 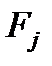, приложенной к j-ому поступательно движущемуся элементу

,

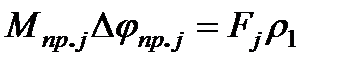откуда

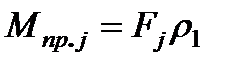. (2.16)

Полученные формулы приведения позволяют при известных параметрах элементов кинематической схемы сделать переход к расчетной приведённой системе. Будем считать заданными силы и моменты, действующие в механической системе (их значение можно рассчитать для конкретных механизмов), а также известны­ми конструктивные размеры и материалы элементов кинематиче­ской цепи. Последние данные позволяют с помощью справочной литературы рассчитать их моменты инерций и эквивалентные же­сткости.

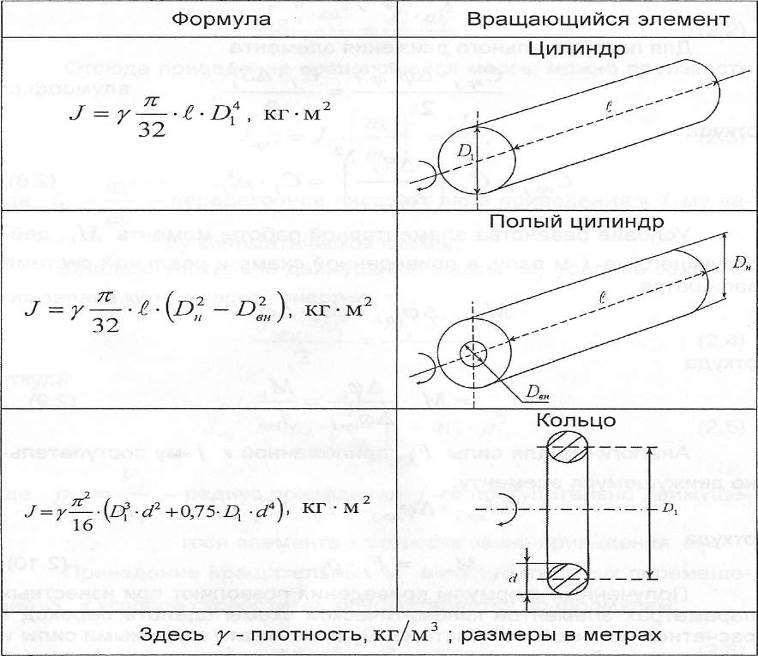
Например, формулы определения моментов инерции неко­торых вращающихся тел приведены в табл. 2.1.

Коэффициенты жесткостей для упругих связей (Нм):

стержня при его растяжении и сжатии

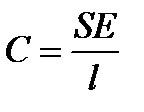Нм, (2.17)

где 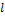– длина стержня, м;

S –площадь поперечного сечения , ;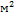

E – модуль упругости растяжения и сжатия, Па;

вала при его скручивании

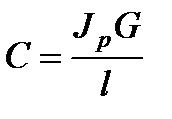, Нм (2.18)

где 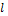– длина вала, м;

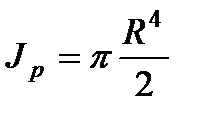- момент инерции поперечного сечения вала, ;

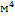R – радиус вала, м;

G – модуль упругости сечения, Па.

Таблица 2.1 Моменты инерции

После приведения к расчетной скорости значений моментов инерций и поступательно движущихся масс, жесткостей, моментов, сил составляется расчетная схема. Для наглядности расчетная схема представляется в виде длинного безинерционного вала, в разных точках которого размещены сосредоточенные массы дви­гателя 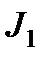, ведущей 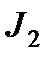и ведомой 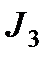полумуфты, ведущей шес­терни , … …

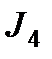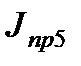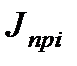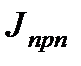, приведённые массы поступательно движущихся элементов 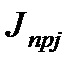… 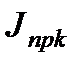(рис. 2.9,б).

Представления о моментах инерций дают размеры соответ­ствующих элементов схемы, изображающих массы, а жесткости 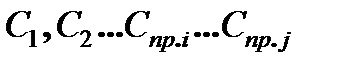обратно пропорциональны длине соответст­вующих отрезков валов.

Для кинематической схемы на рис. 2.9,а приведённая рас­чётная схема имеет вид, показанный на рис. 2.9,б. Необходимо отметить, что расчетная схема электропривода механизма подъё­ма с учётом упругих механических связей представляет собой дос­таточно сложную многомассовую систему. Рассматривая эту схе­му, можно выделить три наиболее значительные массы – ротор двигателя с моментом инерции 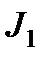, барабан с приведённым мо­ментом инерции 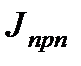и груз 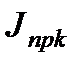. Малые инерционные элемен­ты необходимо добавить к близлежащим большим, а затем определить эквивалентные жёсткости связей между полученными связями по формуле

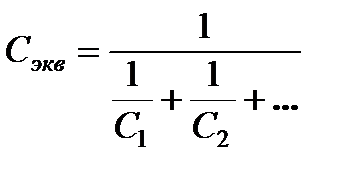. (2.19)

На исходной расчётной схеме стрелками показаны приложен­ные к отдельным массам системы приведённые моменты дейст­вующих внешних моментов (сил) 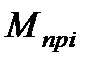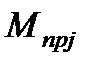. К ротору двигателя приложен электромагнитный момент M и момент потерь .

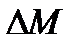Можно рассмотреть ряд примеров составления схем и пока­зать, что совершенно разнотипные механизмы приводятся к трём типовым расчётным схемам (рис. 2.10):

1. Трёхмассовая упругая система.

2. Двухмассовая упругая система.

3. Обобщённое жесткое приведённое механическое звено.

Трёхмассовая упругая система при рассмотрении электро­механических систем (ЭМС) автоматизированного электропривода используется в редких случаях, когда возникает необходимость более детального анализа условий движения их механической части (рис. 2.10,а).

ЭМС автоматизированного электропривода с двухмассовой упругой механической частью представляет собой основной объ­ект, изучаемый в теории автоматизированного электропривода (рис. 2.10,б).

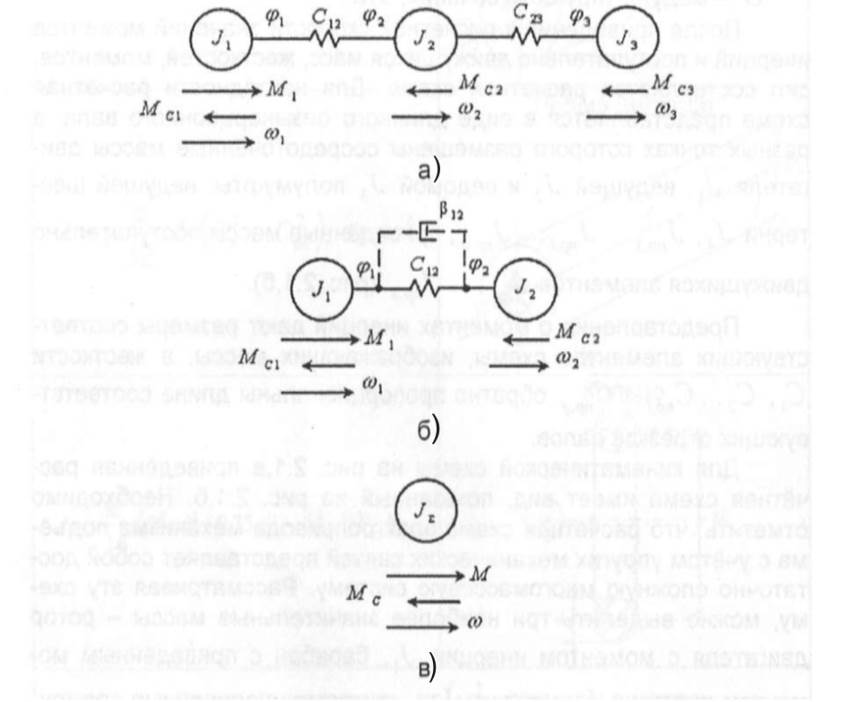Рис. 2.10. Расчетные схемы механической части электропривода

Обобщенное жесткое приведенное механическое звено электропривода может быть представлено схемой рис. 2.10,в. При использовании этой схемы механические связи получаются абсо­лютно жесткими и механическая часть представляется эквива­лентной массой с моментом инерции 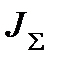, на которую воздейст­вует электромагнитный момент М и суммарный приведенный к валу двигателя момент сопротивлений М_с, включающий все ме­ханические потери в системе, в том числе и механические потери в двигателе.

В общем случае суммарный момент инерции может быть оп­ределен

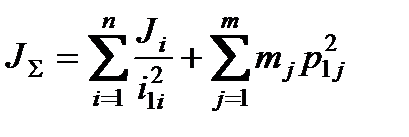, (2.20)

где n и m – число масс установки, соответственно вращающихся и движущихся поступательно.

Если , то

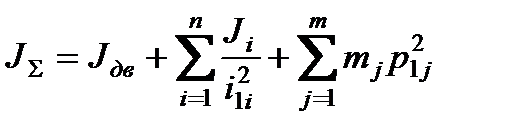. (2.21)

Суммарный, приведённый к валу двигателя момент сопротивлений можно в общем виде записать

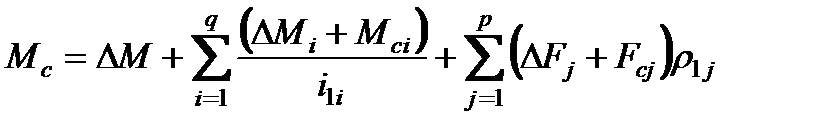, (2.22)

где q – число вращающихся элементов, к которым приложены моменты потерь 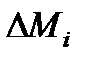, моменты полезной нагрузки ;

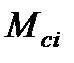p – число поступательно-движущихся элементов с приложенными силами потерь на трение 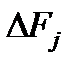и силами полезной нагрузки .

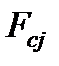После приведения всех сил и моментов

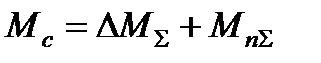, (2.23)

где 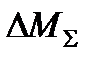- суммарный приведённый момент потерь в агрегате, включая момент механических потерь в двигателе;

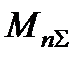- суммарный приведённый момент нагрузки.

Формула для определения 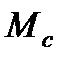удобна для использования в тех случаях, когда все действующие в механизме силы и моменты определены. Обычно потери на трение в механизме неизвестны и для их учёта используется КПД механизма

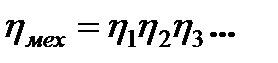, (2.24)

где 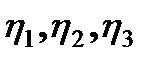- КПД элементов кинематической цепи.

Баланс мощности

,

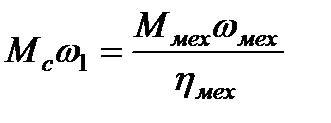откуда

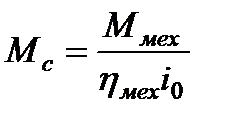, (2.25)

где 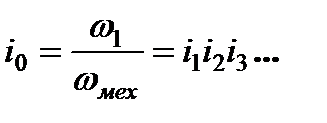- общее передаточное число от двигателя к рабочему органу механизма.

При обратной передаче

.

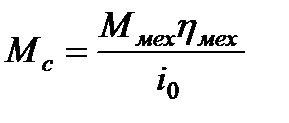Поступательное движение приводится к вращательному

.

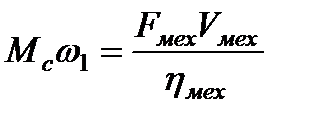Откуда

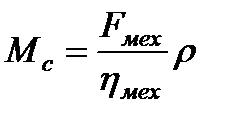. (2.26)

При обратной передаче энергии

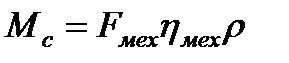. (2.27)