Кривые второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат:
Ах2 +2Вху + Су2 + 2Dx + 2Ey + F = 0.(12)
1. Уравнение окружности с центром в точке О(а,в) и радиусом,
равным R: (х – а)2 + (у – в)2 = R2.
2. Эллипс. Эллипсом называется геометрическое место точек плоскости
(рис.2), для каждой из которых сумма расстояний до двух данных точек
(фокусов) той же плоскости есть постоянная величина, и эта величина
больше расстояния между фокусами.
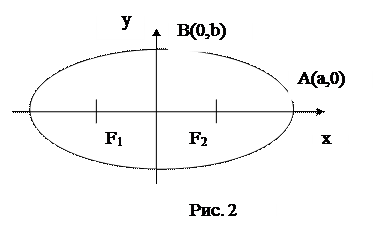
Каноническое уравнение эллипса:

где a = OA – большая , b =
OB - малая полуоси. Координаты фокусов эллипса:
 ,
,
где  .
.
Эксцентриситетом эллипса е называют отношение фокусного расстояния 2с к длине большей оси 2а:
 .
.
Фокальным радиусом точки М эллипса называют отрезки прямых, соединяющих эту точку с фокусами F1 и F2 . Их длины r1 и r2 можно вычислить по формулам:
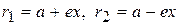 .
.
3. Гипербола. Гиперболой называется геометрическое место точек плоскости (рис. 3), для каждой из которых модуль разности расстояний до двух данных точек (фокусов) той же плоскости есть величина постоянная, и эта величина меньше расстояния между фокусами.Каноническое уравнение гиперболы:
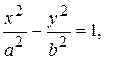
где a = OA – большая , b = OB – малая полуоси.
Координаты фокусов эллипса:

где 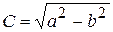 .
.
Эксцентриситетом эллипса е называют отношение фокусного расстояния 2с к длине большей оси 2а:
 .
.
Асимптотами гиперболы называют прямые, определяемые уравнениями:
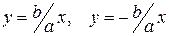 .
.
Директрисами гиперболы называют прямые определяемые уравнениями:
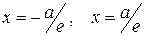 .
.
Гипербола с равными полуосями (b=a) называется равносторонней, ее каноническое уравнение имеет вид
 .
.
Фокальные радиусы точки правой ветви гиперболы вычисляются по формулам:
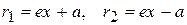 .
.
Фокальные радиусы точки левой ветви гиперболы вычисляются по формулам
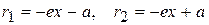 .
.

 y
y
 |  | ||||
 | |||||

 |
F1 F F2 F2 x
Рис. 3
4. Парабола. Параболой называют геометрическое место точек плоскости, равноудаленных от данной точки (Фокса) и данной прямой (директрисы), лежащих в той же плоскости.Уравнение параболы, симметричной относительно оси Ох (рис. 4) и проходящей через начало координат, имеет вид
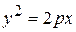 ,
,
уравнение ее директрисы:
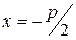 .
.
Парабола, определяемая уравнением, имеет фокус F(p/2,0), фокальный радиус ее точки M(x,y) вычисляется по формуле
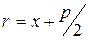 .
.
 у
у

 y
y
 0 х
0 х
 |
0 х
Рис. 4 Рис. 5
Парабола, симметричная относительно оси Oy (рис. 5) и проходящая через начало координат, определяется уравнением
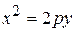 .
.
Пример 18. Привести к каноническому виду уравнение линии
х2+4у2+2х-16у+13= 0 и построить ее.
Решение. Дополним члены, содержащие х,и у, до полных квадратов. Получим(х2 + 2х + 1) + 4(у2 - 4у + 4)-1-16 +13 = 0, или (х +1)2 + 4(у -2)2 = 4,
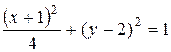 , т.е. эллипс, центр которого лежит в точке С (-1,2), большая полуось а = 2, малая полуось b = 1 ( рис. 6).
, т.е. эллипс, центр которого лежит в точке С (-1,2), большая полуось а = 2, малая полуось b = 1 ( рис. 6).






 y
y
 |
-2 -1 0 x
Рис. 6
Введение в анализ
Пусть два непустых множества Х и У. Если каждому элементу х из множества Х по определенному закону f ставится в соответствие один и только один элемент у из У, то говорят, что задана функция f(x).
Основными элементарными функциями называются следующие функции:
а) степенная функция у = хa, где aÎR;
б) показательная функция у = а х, где а > 0, а ¹ 1;
в) тригонометрические функции;
г) обратные тригонометрические функции.
д) логарифмическая функция у = log a x, где а > 0, а ¹ 1.
Графики основных элементарных функций приведены в прил. 3
Пределы
Числовой последовательностью называется функция х n = j (n), n = =1,2,3,…определенная на множестве натуральных чисел. Число а называется пределом последовательности {хn}, если для любого числа e > 0 найдется такое натуральное число N, что при всех n > N выполняется неравенство 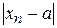 < e.
< e.
Окрестностью точки а называется интервал (а - e; а + e) и обозначают Ue (а). Если число а является пределом последовательности {хn}, то в Ue (а) попадают все члены данной последовательности, кроме конечного их числа.
Последовательность, имеющая предел называется сходящейся. Последовательность, у которой нет предела называется расходящейся.
!Ñ Хорошим примером последовательности является наращивание денежной суммы, положенные в банк. В банк сделан вклад 1000 рублей при процентной ставке 2%. Сумма S которая будет получена через время t при условии начисления простых процентов, выражается формулой S = 1000(1 +0,02 t). Если начисления производятся только по прошествии целого числа лет, то сумма является арифметической прогрессией.
Число А называется пределом функции y=f(x) при 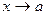 , если для любого e >0 существует
, если для любого e >0 существует  , такое, что | f (x) – A | < ε при 0<| x - а | <
, такое, что | f (x) – A | < ε при 0<| x - а | <  . Записывается:
. Записывается: 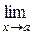 f (x) = A . Аналогично
f (x) = A . Аналогично 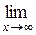 f (x) = A, если | f (x) – A | < ε при
f (x) = A, если | f (x) – A | < ε при 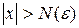 . Употребляется также условная запись
. Употребляется также условная запись 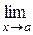 f (x) = ∞, которая обозначает, что
f (x) = ∞, которая обозначает, что 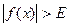 при 0<| x - а | <
при 0<| x - а | < 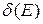 , где Е – произвольное положительное число.
, где Е – произвольное положительное число.
Если с – постоянная величина, то 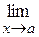 c = c. Если функции f(x) и j(x) имеют пределы при х®а, то
c = c. Если функции f(x) и j(x) имеют пределы при х®а, то
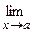 (f(x) ± j(x)) =
(f(x) ± j(x)) = 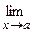 f(x) ±
f(x) ± 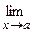 j(x),
j(x),
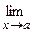 (f(x)·j(x)) =
(f(x)·j(x)) = 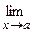 f(x)·
f(x)· 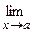 j(x),
j(x),
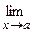
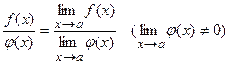 .
.
Односторонние пределы.Если x < а и x → а, то условно пишут x → а - 0; аналогично, если x > а и x → а, то это записывается так x → а +0. Числа f (a - 0) =  f (x) и f (a + 0) =
f (x) и f (a + 0) =  f (x) называются соответственно пределом слева функции f (x) в точке а и пределом справа функции f (x) в точке а (если эти числа существуют).
f (x) называются соответственно пределом слева функции f (x) в точке а и пределом справа функции f (x) в точке а (если эти числа существуют).
Бесконечно малые и бесконечно большие. Если lim α (x) = 0 , т. е. если | α (x) | < ε при 0 < | x – a | < δ (ε), то функция α (x) называется бесконечно малой при x → a. Аналогично определяется бесконечно малая α (x) при x → ∞.
Сумма и произведение ограниченного числа бесконечно малых при x →a есть также бесконечно малые при x → a. Если α (x) и β (x) – бесконечно малые при x → a и 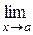
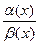 = С,где С – некоторое число, отличное от нуля, то функции α (x) и β (x) называются бесконечно малыми одного и того же порядка; если же С = 0, то говорят, что функция α (x) есть бесконечно малая высшего порядка по сравнению с β (x).
= С,где С – некоторое число, отличное от нуля, то функции α (x) и β (x) называются бесконечно малыми одного и того же порядка; если же С = 0, то говорят, что функция α (x) есть бесконечно малая высшего порядка по сравнению с β (x).
Функция α (x) называется бесконечно малой порядка n по сравнению с функцией β (x), если 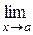
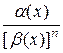 = С, где 0 < | C | < + ∞ .
= С, где 0 < | C | < + ∞ .
Если 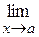
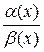 = 1, то функции α (x) и β (x) называются равносильными (эквивалентными) бесконечно малыми при x → a:
= 1, то функции α (x) и β (x) называются равносильными (эквивалентными) бесконечно малыми при x → a:
α (x) ~ β (x).
Например, при х → 0 имеем: sin x ~ x; .tg x ~ x; ln (1 + x) ~ x и т. п.
Замечание. При нахождении предела заменять эквивалентными бесконечно малыми функциями можно только множители и делители.
Если для любого сколь угодно большого числа N существует такое
δ (N), что при 0 < | x – a | < δ (N) выполнено неравенство | f (x) | > N, то функция f (x) называется бесконечно большой при x → а.
Аналогично определяется бесконечно большая f (x) при x → ∞. Подобно тому, как это сделано для бесконечно малых, вводится понятие бесконечно больших различных порядков.
Некоторые важные пределы:
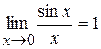 - первый замечательный предел;
- первый замечательный предел;
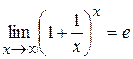 - второй замечательный предел;
- второй замечательный предел;
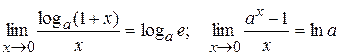 ;
; 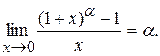
Пример 19. Найти пределы:
1)  ; 2)
; 2) 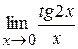 ; 3)
; 3) 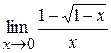 ;
;
4) 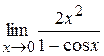 ; 5)
; 5) 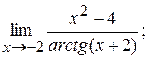
6) 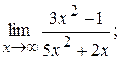 7)
7) 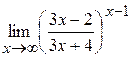 .
.
Решение:
1. Разлагаем числитель и знаменатель дроби на множители, как квадратные трехчлены, по формуле ax2 +bx+c = a(x-x1)(x-x2) ,
где х1 и х2 – корни трёхчлена. Тогда
 =
= 
2. Выяснив вначале, что при указанном изменении аргумента данная функция представляет отношение двух бесконечно малых величин (случай 0/0), перейдем к эквивалентным функциям:
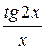 =
= 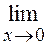
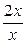 = 2.
= 2.
3. Уничтожаем иррациональность в числителе путём умножения числителя и знаменателя на 1+ 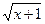 , затем сокращаем дробь на х:
, затем сокращаем дробь на х:



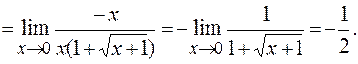
4. Применяем тригонометрическую формулу: 1 – cos x = 2sin2 
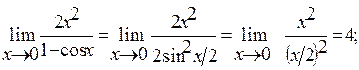
5. 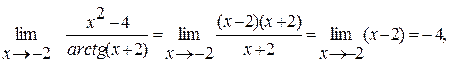 так как arctg (x+2)
так как arctg (x+2)  (x+2).
(x+2).
6. Убедившись, что имеет место случай 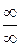 , подвергаем функцию преобразованиям. Делим числитель и знаменатель дроби на х2 (наивысшая здесь степень х
, подвергаем функцию преобразованиям. Делим числитель и знаменатель дроби на х2 (наивысшая здесь степень х 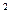 ), находим:
), находим:

 так как при х
так как при х 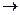 ¥ величины 1/х2 и 1/х являются бесконечно малыми.
¥ величины 1/х2 и 1/х являются бесконечно малыми.
7. При х 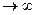 основание степенно-показательной функции
основание степенно-показательной функции
f(x) = 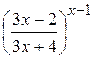 стремится к 1, т.к.
стремится к 1, т.к.  , а показатель степени есть бесконечно малая функция. Таким образом имеем неопределенность вида
, а показатель степени есть бесконечно малая функция. Таким образом имеем неопределенность вида 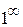 . Сведем этот предел ко второму “замечательному пределу “:
. Сведем этот предел ко второму “замечательному пределу “:
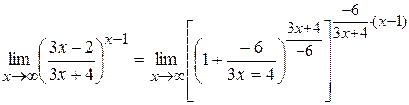 =
= 
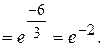
5.2. Непрерывность функций
Функция f (x) называется непрерывной в точке а, если:
1) эта функция определена в точке а, т. е. существует число f (а);
2) существует конечный предел 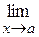 f (x);
f (x);
3) этот предел равен значению функции в точке а, т. е. 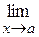 f (x) = f (а).
f (x) = f (а).
Говорят, что функции f (х) терпит разрывы непрерывности при значении х = х0 (или в точке х0), принадлежащем области определения функции или являющемся граничным для этой области, если в этой точке нарушается условие непрерывности функции. Например, функция
f (x) = 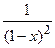 разрывна при х = 1. Эта функция не определена в точке х =1, и как бы мы ни выбрали число f (1), пополненная функция f (x) не будет непрерывной при х = 1. Если для функции f (x) существуют конечные пределы:
разрывна при х = 1. Эта функция не определена в точке х =1, и как бы мы ни выбрали число f (1), пополненная функция f (x) не будет непрерывной при х = 1. Если для функции f (x) существуют конечные пределы:
 f (х) = f (х0 – 0) и
f (х) = f (х0 – 0) и 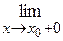 f (x) = f (х0 + 0) ( причем не все три числа f (х), f (х0 – 0), f (х0 + 0) равны между собой), то х0 называется точкой разрыва 1-го рода. В частности, если f (х0 – 0) = f (х0 + 0), то х0 называется устранимой точкой разрыва. Для непрерывности функции f (x) в точке х0 необходимо и достаточно, чтобы
f (x) = f (х0 + 0) ( причем не все три числа f (х), f (х0 – 0), f (х0 + 0) равны между собой), то х0 называется точкой разрыва 1-го рода. В частности, если f (х0 – 0) = f (х0 + 0), то х0 называется устранимой точкой разрыва. Для непрерывности функции f (x) в точке х0 необходимо и достаточно, чтобы
f (х0) = f (х0 – 0) = f (х0 + 0).
Точки разрыва функции, не являющиеся точками разрыва 1-го рода , называются точками разрыва 2-го рода. К точкам разрыва 2-го рода относятся также точки бесконечного разрыва, т. е. такие точки х0 , для которых хотя бы один из односторонних пределов f (х0–0) или f (х0 + 0) равен ∞.
Функция у = f (х) называется непрерывной в точке х0, если эта функция определена в какой – нибудь точке х0 и если
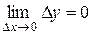 .
.
Пример 20.Исследовать на непрерывность функцию и построить график
 2
2  при
при  0
0 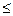 х
х 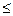 1;
1;
j(х) = 4 - 2х при 1< х <2;
2х – 7 при 2 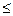 х < +¥.
х < +¥.
Решение. Неэлементарная функция j(х) определена для всех значений х 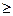 0. Она может иметь разрыв в точках х = 1 и х = 2, где меняется ее аналитическое выражение. Во всех остальных точках своей области определения функция j (х) непрерывна, поскольку каждая из формул, которыми она задана, определяет собой элементарную функцию, непрерывную в своем интервале изменения аргумента х.
0. Она может иметь разрыв в точках х = 1 и х = 2, где меняется ее аналитическое выражение. Во всех остальных точках своей области определения функция j (х) непрерывна, поскольку каждая из формул, которыми она задана, определяет собой элементарную функцию, непрерывную в своем интервале изменения аргумента х.
Исследуем непрерывность в точках х = 1 и х = 2:
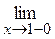 j(х) = lim 2
j(х) = lim 2 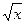 = 2;
= 2; 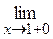 j(x) = lim(4 - 2x) = 2.
j(x) = lim(4 - 2x) = 2.
Согласно условию, значение функции j (х) в точке х =1 определяется первой формулой: j(1) = 2 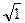 = 2. Следовательно, в точке х =1 выполняются все условия непрерывности: функция определена в окрестности точки х =1 и
= 2. Следовательно, в точке х =1 выполняются все условия непрерывности: функция определена в окрестности точки х =1 и 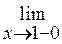
 =
= 
 =
=  . Поэтому в точке х =1 функция j(х) непрерывна.
. Поэтому в точке х =1 функция j(х) непрерывна.
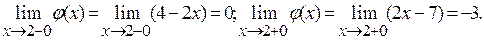
Здесь левый и правый пределы функции конечны, но не одинаковы, т.е. не выполняется 2-е условие непрерывности. Поэтому в точке х=2 функция имеет разрыв (рис 7).
Скачек функции в точке разрыва конечный.
 | |||
 | |||

 у = 4-2х
у = 4-2х
 у =2x – 7
у =2x – 7
 y =2
y =2 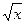

 0 1 2
0 1 2
-3

Рис.7
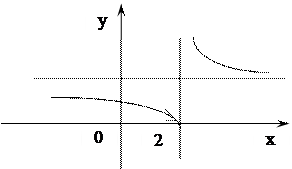
Пример 21. Исследовать функцию 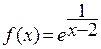 на непрерывность.
на непрерывность.
Решение. Функция непрерывна всюду, за исключением точки х0 = 2 (т.к. элементарные функции непрерывны во всех точках, где они определены). Найдем пределы слева и справа при х → 2:
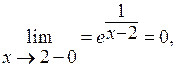
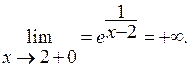
Следовательно, х0 = 2 – точка разрыва II рода. Для схематического построения графика найдем предел функции на бесконечности:  откуда устанавливаем, что прямая
откуда устанавливаем, что прямая
у = 1 – горизонтальная асимптота (рис. 8).
 |
|
Дата добавления: 2020-07-18; просмотров: 589;











