Линейные пространства

Рассмотрим множества V элементов х, y, z,… и множество Rдействительных чисел. Определим операцию сложения элементов множества V: любой упорядоченной паре элементов х Î V, y Î V поставим в соответствие третий элемент zÎ V, называемый их суммой, и запишем в виде z = x + y.

Введем также операцию умножения элементов множества V на действительные числа; каждому элементу х Î Vи действительному числу aÎR поставим в соответствие элемент z = ax = x a, где z ÎV. Потребуем, чтобы операция сложения элементов множества V и операция умножения элементов этого множества на действительные числа удовлетворяли следующим аксиомам:

1. Сложение коммутативно, т.е. х + у = у + х для любых х Î V, y ÎV.
2. Сложение ассоциативно, т.е. (х + у) + z = x + (у + z) для любых х Î V, yÎV, zÎV.
3. Существует нулевой элемент, т.е. такой элемент, который в сумме с любым элементом х дает тот же элемент х; обозначим этот элемент символом 0, тогда х + 0 = х для любого х Î V.
4. Для каждого элементах Î Vсуществует противоположный элемент, т.е. такой элемент, который в сумме с данным дает нулевой элемент; элемент, противоположный элементу х, обозначим через – х, тогда

х + (-х) = 0 для любого х Î V.

1. Умножение на число 1 не меняет элемента, т.е. 1×х = х для любого хÎ V.

Длялюбых х, y ÎV, a, b Î R:

1. .
2. .
3. .

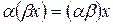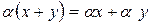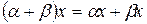Множество V элементов х,y,z,…, в котором определены операции сложения и умножения элемента на действительное число, удовлетворяющие аксиомам 1 – 8, называется действительным линейным пространством или действительным векторным пространством. Элементы действительного пространства называют векторами.

Векторы 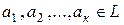называются линейно зависимыми, если существуют числа 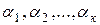, не все равные нулю и такие, что

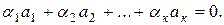(8)

Если равенство (8) выполняется только при 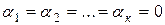, то векторы 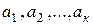называются линейно независимыми. Базисом n – мерного пространства называется любая упорядоченная система n линейно независимых векторов этого пространства. Базис пространства V₃ образует любая тройка некомпланарных векторов, так как эти векторы линейно независимы и любая четверка векторов линейно зависима.

Линейное пространства L называется n - мерным, если в нем существуют n линейно независимых векторов, а всякие n+1 векторов являются линейно зависимыми. Число n называется в этом случае размерностью линейного пространства L, которое обозначают dim L. Итак, размерность линейного пространства – это наибольшее возможное количество линейно независимых элементов в нем. Линейное пространство, в котором имеется базис, состоящий из конечного числа векторов, называется конечномерным. Линейное пространство называется бесконечномерным, если при любом натуральном числе m в нем найдется m линейно независимых векторов.

Теорема. Если е₁, е₂,…, е_n – базис линейного n – мерного пространства V_n, то любой вектор х этого пространства линейно выражается через базисные векторы е₁, е₂,…, е_n, т.е.

х = 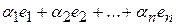. (9)

Коэффициенты a₁, a₂, …, a_n этого разложения определяются однозначно. Выражение (9) называется разложением вектора хпо базису е₁, е₂,…, е_n. Координатами вектора х в базисе е₁, е₂,…, е_n называются коэффициенты a₁, a₂, …, a_n в разложении этого вектора по данному базису. Координаты вектора, очевидно, зависят от выбора базиса. Координаты одного и того же вектора будут различными в разных базисах. Задача преобразования координат вектора состоит в нахождении зависимости между координатами данного вектора в разных базисах, связь между которыми известна. Формулами преобразования координат называют формулы, связывающие координаты вектора в разных базисах.

В линейном n – мерном пространстве V_n фиксируем два базиса:

е₁, е₂, …, е_n (*)

е₁^*, е₂^*,…, е_n^* (**)

Матрицей перехода от базиса (*) к базису (**) называется матрица системы векторов (**) в базисе (*). Каждый вектор системы (**) можно разложить по базису (*). Пусть

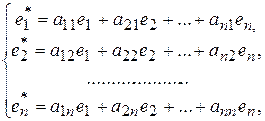
тогда матрица перехода от базиса (*) к базису (**) имеет вид

А = 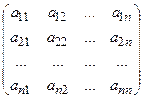. (10)

Матрица перехода от одного базиса к другому будет невырожденной, всякую невырожденную матрицу n – го порядка можно рассматривать как матрицу перехода от одного базиса линейного n – мерного пространства к другому базису этого пространства. Матрица А ^{- 1}, обратная матрице (10), является матрицей перехода от базиса (**) к базису (*).

Теорема.Если х₁, х₂,…, х_n - координаты вектора х в базисе

е₁, е₂, …, е_n, х₁^*, х₂^*,…, х_n^* - координаты того же вектора в базисе е₁^*, е₂^*,…, е_n^* то Х = АХ^*, где

,

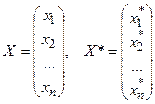А – матрица перехода от базиса е₁, е₂, …, е_n к базису е₁^*, е₂^*,…, е_n^*.

Пример 12.Доказать, что векторы е₁ = (1,3,-2), е₂ = (2,-5,1),

е₃ = (1,3,-1) образуют базис в R³ и найти координаты вектора х= (1,2,3) в этом базисе.

Решение.

Проверим, что векторы е₁,е₂,е₃ линейно независимы. Проверяем равенство (8), оно равносильно системе линейных уравнений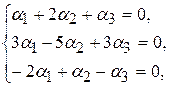

Вычислим определитель

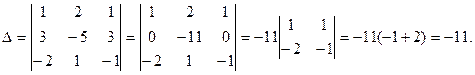
Определитель отличен от нуля, следовательно, система имеет единственное решение: 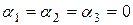. Поэтому векторы е₁, е₂, е₃ линейно независимы. Обозначим через В = 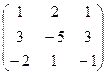матрицу перехода от старого базиса к новому. Найдем В^-1:

D= -11, В₁₁ = 2, В₂₁ = 3, В₃₁ =11, В₁₂ = -3, В₂₂ = 1, В₃₂ = 0, В₁₃ = -7, В₂₃ = -5, В₃₃ = -11. .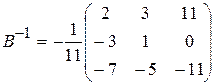

Откуда 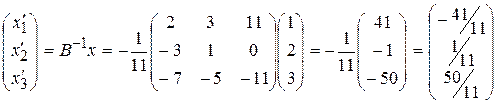, т.е.

x= .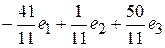

3.2.Линейные преобразования.

Если указано правило, по которому каждому вектору х линейного пространства V ставится в соответствие единственный вектор у этого пространства, то говорят, что в нем задано преобразование f.

Преобразование fлинейного пространства V называется линейным преобразованием, если для любых векторов этого пространства х₁, х₂. х₃ и любого действительного числа l выполняются следующие условия:

1) f(x₁+x₂)= f(x₁)+f(x₂);

2) f(lx)= lf(x).

Линейные преобразования полностью характеризуются его матрицей. Поэтому действия над такими преобразованиями сводятся к действиям над матрицами. Например, если вектор х переводится в вектор у линейным преобразованием с матрицей А, а вектор у переводится в вектор zлинейным преобразованием с матрицей В, то последовательное применение этих преобразований равносильно линейному же преобразованию, переводящему вектор х в вектор z. Матрица этого линейного преобразования С = АВ.

Ненулевой вектор х линейного пространства называется собственным вектором линейного преобразования f этого пространства, если существует число k такое, что

f(x) = kx,

причем k - действительное число для действительного линейного пространства и комплексное число в случае комплексного пространства. Число k называют собственным значением вектора х относительно преобразования f.Данное равенство можно записать в матричной форме:

АХ = kХ,

где А – матрица преобразования f в некотором базисе; Х – матрица- столбец из координат собственного вектора х в том же базисе.

Собственные векторы и собственные значения обладают следующими свойствами:

1. Собственный вектор линейного преобразования имеет единственное собственное значение к.

2. Если х– собственный вектор линейного преобразования f с собственным числом к и l - любое, отличное от нуля число, то lх – также собственный вектор преобразования f с собственным значением к.

3. Если х и у – линейно независимые собственные векторы линейного преобразования f c одним и тем же собственным значением к, то х +у – также собственный вектор этого преобразования с собственным значением к.

Собственными значениями линейного преобразования действительного пространства являются только действительные корни характеристического уравнения.

Пример 13.Найти действительные собственные значения и собственные векторы линейного преобразования с матрицей

А = .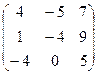

Решение. Составляем характеристическое уравнение матрицы А

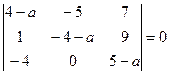или а³- 5а² +17а - 13 = 0.

Разложим на множители многочлен в левой части уравнения:

а³-5а²+17а -13 = а³- а² - 4а² + 4а +13а -13 = а²(а -1) - 4а(а-1) + 13(а-1) =

= (а -1)(а² - а +13). Уравнение примет вид (а-1)(а² - 4а +13) = 0, откуда а₁ = 1, а₂ = 2 -3i, а₃ = 2 +3i. Следовательно, линейное преобразование с данной матрицей имеет только одно действительное собственное значение а = 1.

Для отыскания соответствующего собственного вектора составляем систему уравнений:

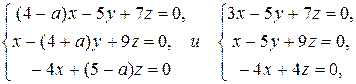при а = 1.

Решая данную систему, находим х = z, х = 2z. Полагая z = 1, получаем собственный вектор: х = (1, 2, 1).