Элементы векторной алгебры
2.1. Векторы, основные понятия.
1. Нахождение модуля вектора а = (х,у,z): 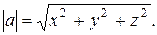
a) Нахождение координат вектора 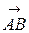 по двум точкам А (ха,уа,za) и
по двум точкам А (ха,уа,za) и
В (хв,ув,zв): 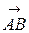 (хв- ха, ув- уа,zв- za).
(хв- ха, ув- уа,zв- za).
3. Если С- середина отрезка АВ, то
х с = 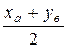 ,
, 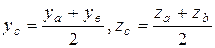 .
.
4. Проекция вектора на ось: прl АВ= 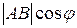 , где j - угол между вектором АВ и ось l.
, где j - угол между вектором АВ и ось l.
5. Направляющие косинусы вектора. Пусть 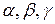 - углы, которые образует вектор
- углы, которые образует вектор 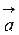 =(х,у,z) с координатными осями. Косинусы этих углов называются направляющими косинусами:
=(х,у,z) с координатными осями. Косинусы этих углов называются направляющими косинусами:
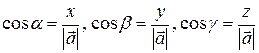 .
.
2.2. Скалярное произведение
Скалярным произведением двух векторов 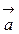 и
и 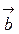 называется число, равное произведение модулей векторов на косинус угла между ними:
называется число, равное произведение модулей векторов на косинус угла между ними:
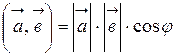 .
.
Скалярное произведение обладает свойствами:
1) переместительным 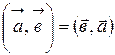 ;
;
2) сочетательным 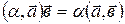 ;
;
3) распределительным 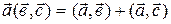 ;
;
4) скалярным квадратом 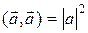 ;
;
5) если векторы перпендикулярны, то 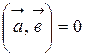 .
.
Если даны векторы 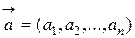 и
и 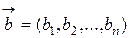 , то их скалярное произведение можно вычислить по формуле
, то их скалярное произведение можно вычислить по формуле
( 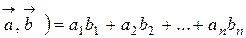 .
.
Углом между двумя векторами 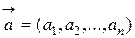 и
и 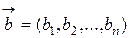 называют угол φ (0≤φ≤ π), определяемый из уравнения
называют угол φ (0≤φ≤ π), определяемый из уравнения
|
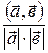 .
.
2.3. Векторное произведение векторов
Векторным произведением вектора 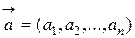 на вектор
на вектор 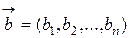 называется вектор
называется вектор 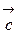 :
:
а) 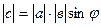 ;
;
б) вектор 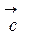 перпендикулярен к плоскости параллелограмма,
перпендикулярен к плоскости параллелограмма,
построенного на векторах аи в как на сторонах;
в) направлен так, что кратчайшее вращение вектора 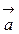 к вектору
к вектору 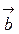 мы наблюдаем с конца вектора
мы наблюдаем с конца вектора 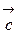 совершающимся против часовой стрелки (говорят также, что
совершающимся против часовой стрелки (говорят также, что 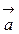 ,
, 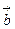 ,
, 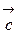 – правая связка).
– правая связка).
Векторное произведение обозначают 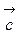 =
= 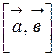 .
.
Векторное произведение двух векторов обладает свойствами:
1) 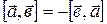 ;
;
2) 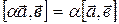 ;
;
3) 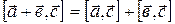 ;
;
4) если векторы коллинеарны, то 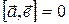 .
.
Если 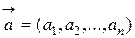 и
и 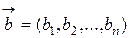 , то
, то 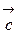 =
= 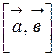 можно вычислить по формуле
можно вычислить по формуле
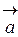
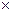
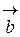 =
= 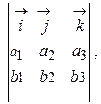
где 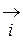 ,
, 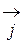 ,
, 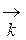 - единичные векторы, направленные соответственно по осям Ох1, Ох2, Ох3 (естественный базис в R3).
- единичные векторы, направленные соответственно по осям Ох1, Ох2, Ох3 (естественный базис в R3).
Площадь треугольника АВС определяется по формуле
S = 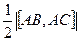 .
.
Дата добавления: 2020-07-18; просмотров: 502;











