Апериодическое звено второго порядка.

Дифференциальное уравнение имеет вид:

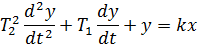
При этом корни характеристического уравнения 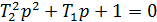должны быть вещественными, что будет выполняться при условии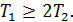

Апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени.

Примеры апериодических звеньев второго порядка приведены на рис.5.Рассмотрим подробно случай двигателя постоянного тока(рис.5, а). При отсутствии момента нагрузки на валу и при учете переходных процессов в цепи якоря динамика двигателя описывается двумя уравнениями, определяющими равновесие э. д. с. в цепи якоря:

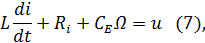
и равновесие моментов на валу двигателя:

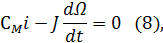
где u – напряжение, прикладываемое к якорю, C_E и C_M – коэффициенты пропорциональности между обратной э. д. с. и скоростью вращения Ω и между вращающим моментом и током якоря i, J – приведенный момент инерции, L и R -индуктивность и сопротивление цепи якоря.

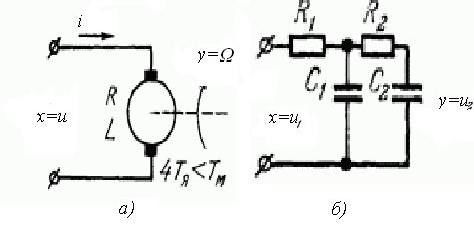
Рис. 5. Примеры апериодических звеньев второго порядка: а) двигатель постоянного тока, б)R-C цепь

Решаем совместно, т.е. выражаем ток i из уравнения (8) и подставляем его в уравнение (7):

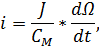
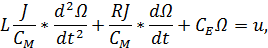
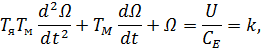
где .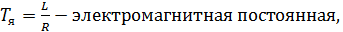

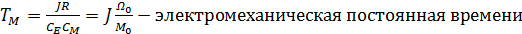Аналогично можно получить дифференциальное уравнение для случая на рис 5, б.