Взаимосвязь определителей большего и меньшего порядка. Разложение по строке.

Запишем разложение определителя порядка 3.

= .

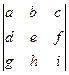Вынесем за скобку элементы первой строки (они есть в 2 из 6 слагаемых): .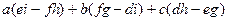

То, что получилось в скобках, называют алгебраическими дополнениями элементов соответственно .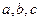

Выражение в 1-й скобке 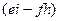называется алгебраическим дополнением к элементу , соответственно

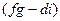- алгебраическим дополнением к 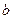, 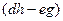- алгебраическим дополнением к .

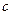Заметим, что , , .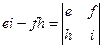

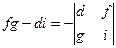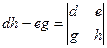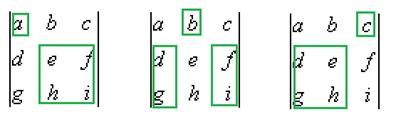
Если для элемента 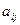и вычеркнуть всю строку и весь столбец, где он находится, образуется подматрица порядка (n-1). Определитель подматрицы порядка (n-1), которая получилась путём вычёркивания строки номер i и столбца номер j, называется дополняющим минором к элементу 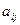. Всего таких миноров 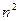, например для матрицы 3 порядка их будет 9 штук. Минор, соответствующий элементу 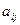, обозначается .

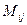Мы видим, что в одних случаях алгебраическое дополнение равно минору, а где-то противоположно ему по знаку. Взаимосвязь алгебраических дополнений и миноров для произвольных i,j:

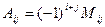, то есть знаки меняются в шахматном порядке, для верхнего левого элемента 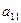знак «+».

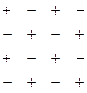
Итак, определители можно вычислять разложением по строке:

= .

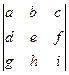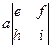
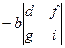
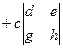Разложение возможно по любой строке или по любому столбцу. Так, например, в той же рассмотренной ранее записи можно собрать пары слагаемых, содержащих 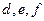и точно так же вынести за скобку, получится = =

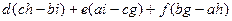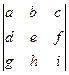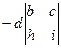
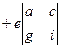
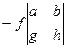= здесь чередование знака начинается с минуса, что и должно быть в соответствии с шахматным порядком, о чём сказано выше.

Лемма. .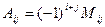

Доказательство.

1) Если для произвольного определителя 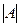собрать отдельно все 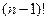членов определителя, в составе которых присутствует 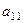, и вынести за скобку 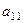, то в скобке получится дополнящий минор (без смены знака). Это объясняется тем, что каждый из членов определителя в такой сумме задаётся перестановкой, имеющей 1 на первом месте: 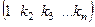. Число инверсий в ней совпадает с числом инверсий перестановки 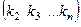, так как 1 ни с каким числом инверсию не образует.

2) Если рассмотреть сумму 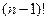членов определителя, в составе которых присутствует 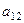, то им соответствуют перестановки вида

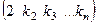ведь в 1-й строке число взято из 2-го столбца. Число инверсий в ней ровно на 1 больше, чем в перестановке 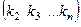, так как среди чисел 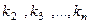есть число 1, и оно образует инверсию с числом 2, расположенным на первом месте.

3) Общий случай. Рассмотрим сумму из 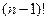членов определителя, в составе которых присутствует 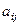. Меняя строки и столбцы, можно добиться того, что это число окажется на месте 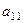. Для этого нужно 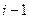раз поменять строку с соседней сверху, а затем 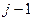раз столбец, где было это число, с соседним слева. При этом будет совершено 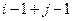операций, то есть исходный определитель умножился бы на 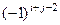, что равно 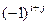. Поэтому .

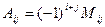Теорема 1. Сумма всех произведений элементов какой-либо строки (столбца) матрицы на их алгебраические дополнения равна определителю матрицы: .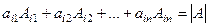

Доказательство.Каждое алгебраическое дополнение состоит из 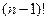слагаемых, так как является (с точностью до знака) определителем матрицы порядка 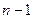. По лемме, .

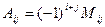В итоге получим 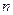сумм по 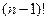слагаемых, то есть как раз 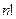. Причём эти множества взаимно не пересекающиеся: для первых 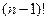в 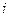-й строке выбираем из 1-го столбца, в следующих из 2-го и т.д.

Теорема 2. Если матрица треугольная, то .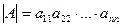

Доказательство.

Пусть дан определитель .

Если разложить его по первому столбцу, где всего один ненулевой элемент и остальные 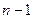нулей, то сразу переходим к минору меньшего порядка:

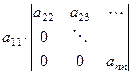+ 0 + ... + 0.

для него получается аналогичное действие, тогда на следующем шаге получаем 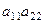умножаются на определитель треугольной матрицы, у которой угловой элемент 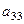. Продолжая этот процесс, получим .

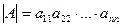Замечание. Для диагональных матриц верен такой же факт, ведь диагональная это частный случай треугольной.

Пример.

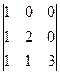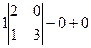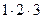= = = = 6.

Приведение к треугольному виду очень часто используется для вычисления определителей. Метод Гаусса, который будет подробно изучен в теме «системы уравнений», в полной мере может применяться и для вычисления определителей. Если обнулить элементы ниже главной диагонали, то вычисление определителя сильно упростится.

Теорема 3. Сумма всех произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) равна 0: .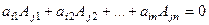

Доказательство.Если числа i-й строки умножаются на алгебраические дополнения к клетке на месте (1,1), (1,2) , ... (1,n)

(ведь алгебраические дополнения не зависят от того, какое число в этой клетке было, а только от расположения), то это всё равно, что в 1-ю строку поставить копии чисел 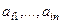и затем вычислить определитель, содержащий две одинаковые строки:

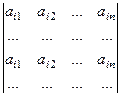
Но такой определитель равен 0, так как две строки одинаковы.

Обобщим метод разложения по строке. Введём понятие дополняющего минора и алгебраического дополнения к минору, а не к элементу. Если выбрать какие-либо 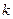строк и 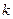столбцов, на пересечении образуется минор порядка 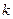, обозначим его 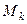. Если вычеркнуть все эти 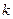строк и 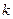столбцов, из оставшихся элементов получится квадратная матрица порядка 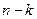. Её определитель называется дополняющим минором к исходному минору, обозначим 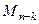. Если выбрать в записи определителя всей матрицы те члены определителя, которые содержат элементы исходного выбранного минора порядка 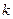, и вынести их за скобку, то останется сумма, которая называется алгебраическим дополнением данного минора.

Теорема 4. Формула взаимосвязи минора и алгебраического дополнения: 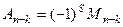, где 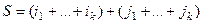, то есть сумма всех номеров выбранных строк и столбцов исходного минора.

Доказательство.

1) Пусть исходный минор расположен в верхнем левом углу.

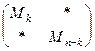докажем, что в этом случае дополняющий минор в точности равен алгебраическому дополнению.

Все те члены определителя матрицы, в которых есть элементы этих миноров 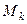и 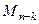, составляют в точности слагаемых.

Причём перестановки, их задающие, содержат числа 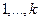в каком-то порядке на первых 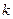местах, и от до 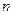на последних 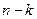местах. Ни одно число из множества 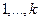не образует инверсию ни с одним числом ,..., . 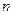То есть, произведение 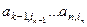, являющееся членом определителя 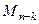, умножается на всякое 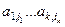из определителя 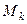без смены знака.

В этом случае, 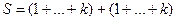очевидно, чётное число.

2) Пусть минор 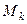расположен на пересечении произвольных строк с номерами 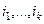и столбцов с номерами 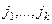. Чтобы переместить его в левый верхний угол, нужно сначала, например, строку 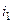переместить на 1-е место, для чего будет нужно 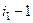транспозиций соседних строк. Затем аналогично сделать с 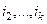. Понадобится 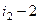действий, чтобы строка с номером 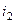перешла на 2-е место, затем вплоть до того, что 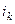на месте k. А после этого такие же действия со столбцами. Общее количество действий:

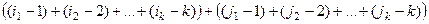
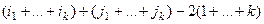= . Последнее вычитаемое - чётное, тогда чётность всего полученного числа совпадает с чётностью числа .

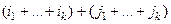Таким образом, чтобы вычислить алгебраическое дополнение к минору 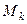, «разбросанному» по матрице, нужно дополняющий минор умножить на 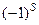, где .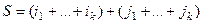

Произведение 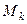на 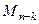содержит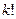 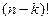членов исходного определителя .

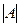Теорема 5 (Лапласа). Пусть в определителе порядка n произвольно выбрано k строк. Тогда сумма произведений всех миноров k-го порядка, содержащихся в выбранных строках, на их алгебраические дополнения, равна .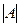

Доказательство.

Количество миноров, содержащихся в k строках, равно числу сочетаний = .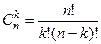

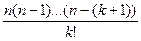Для каждого из них получится сумма 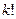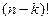членов определителя исходной матрицы 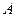. Тогда 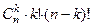= = 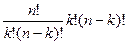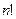членов исходного определителя. При этом именно они все учтены, так как при таком разложении нет повторов: среди всех миноров, выбранных в 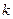строках, каждые 2 отличаются хотя бы одним номером столбца.

Теорема 5 даёт возможность быстро считать определители блочно-диагональных и блочно-треугольных матриц. Например, для примера ниже - нет необходимости искать все 24 набора, достаточно вычислить так:

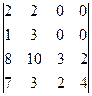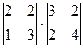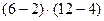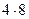= = = = 32.

(В первых двух строках - всего один минор порядка 2).

Теорема 6.Определитель произведения квадратных матриц порядка n равен произведению определителей: .

Доказательство.Построим такую вспомогательную матрицу порядка 2n:

.

По теореме Лапласа, её определитель равен произведению двух миноров порядка n, то есть 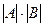, так как в верхних n строках других миноров, отличных от нуля, нет.

Теперь преобразуем матрицу, складывая столбцы (что, очевидно, не ведёт к изменению определителя).

К -у столбцу прибавим 1-й, домноженный на коэффициент 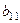, затем 2-й, домноженный на 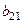, и т.д. до n-го, домноженного на 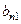. После этого та часть -го столбца, которая ниже n-й строки, станет состоять из нулей. А в верхних n строках получится такая часть столбца:

=

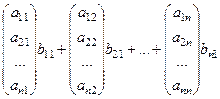но это 1-й столбец произведения матриц: .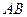

Аналогичными действиями обнуляем 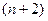-й столбец ниже n-й строки, тогда в верхней части получается 2-й столбец из произведения 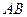. После всех таких действий вместо 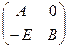получится матрица, состоящая из блоков: 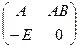. Её определитель равен произведению двух миноров: 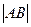и 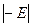, домноженному на 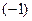в степени 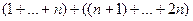, так как это сумма номеров строк и столбцов минора 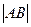. При этом = .

= .

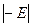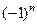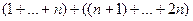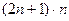Получается, что определитель этой матрицы равен 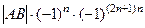= = 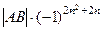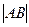, так как 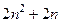чётно.

Итак, = .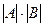

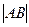§ 3. Обратная матрица.

Определение. Матрица называется вырожденной, если 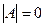, и невырожденной, если .

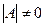Определение. Пусть 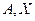- квадратные матрицы. Если 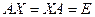то 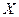называется обратной матрицей для матрицы .

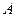Обозначение: Обратная матрица обозначается .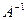

Замечание. Для чисел, которые являются матрицами порядка 1, обратный элемент вычисляется известным образом, например , .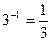

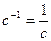Докажем, что не существует различных «обратной слева» и «справа» матриц. Так как коммутативность в общем случае не выполняется, то вовсе не очевидно, что обратная матрица единственна, ведь можно предположить, что левая обратная и правая обратная - различны.

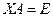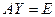Лемма.Если и , то .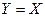

Доказательство.Пусть 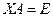и 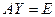. По закону ассоциативности, можно записать такое равенство: .

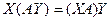Но тогда получается 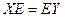, то есть .

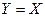Итак, . Но оказывается, что не для любой квадратной матрицы существует обратная.

Теорема 1.Обратная матрица 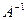существует тогда и только тогда, когда А невырожденная.

Доказательство. Для доказательства рассмотрим 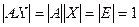. Если 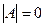то 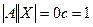, то есть существовало бы такое число, которое при умножении на 0 даёт результат 1, но это невозможно. Получили противоречие.