Исследование функций и построение их графиков

Необходимый признак монотонности:

1) если функция f(x) в интервале возрастает, то ее производная f ¢ (x) неотрицательна.

2) если функция f(x) в интервале убывает, то ее производная f ¢ (x) неположительна.

3) если функция f(x) в интервале не изменяется, то ее производная f ¢ (x) тождественна равна нулю.

Достаточный признак монотонности:

1) если производная f ¢ (x) всюду в интервале положительна, то функция f(x) в этом интервале возрастает;

2) если производная f ¢ (x) всюду в интервале отрицательна, то функция f(x) в этом интервале убывает.

Точка х₀ называется точкой максимума (минимума) функции f(x), если f(x₀) есть наибольшее (наименьшее) значение функции f9x) в некоторой окрестности точки х₀. Точки максимума и минимума функции называются точками экстремума.

Необходимый признак экстремума: если в точке х₀ функция f(x) достигает экстремума, то ее производная в этой точке либо равна нулю, либо не существует.

Достаточный признак экстремума: точка х₀ является точкой экстремума функции f(x), если производная f ¢ (x) при переходе х через х₀ меняет знак; при перемене знака “+” на “–“ точка х₀ является точкой максимума; при перемене “–“ на “+” точка х₀ является точкой минимума.

График функции называется выпуклым в данном промежутке, если он лежит ниже любой своей касательной; вогнутым, если он лежит выше любой своей касательной (рис. 9 и 10).

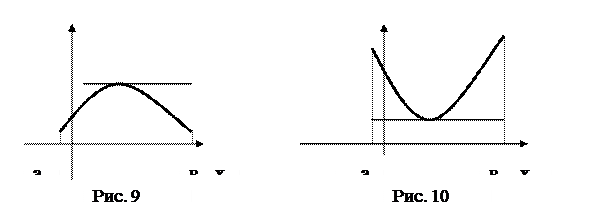
Точкой перегиба называется точка, отделяющая выпуклую дугу от вогнутой.

Признак выпуклости и вогнутости линии: если вторая производная f ² (x) всюду в интервале отрицательна, то дуга линии у = f(x), соответствующая этому интервалу, выпуклая. Если вторая производная f ² (x) всюду в интервале положительна, то дуга линии у = f(x), соответствующая этому интервалу, вогнутая.

Необходимый признак точки перегиба: если х₀ – абсцисса точки перегиба, то либо f ² (x₀) = 0, либо f ² (x₀) не существует.

Достаточный признак точки перегиба: точка (х₀,у₀) есть точка перегиба линии у = f(x), если f ² (x) меняет знак при переходе х через х₀.

Асимптоты линии: прямая линия g называется асимптотой линии L, если расстояние точки линии L от прямой g стремится к нулю при неограниченном удалении этой точки от начала координат.

Следует различать вертикальные и наклонные асимптоты:

1) Если 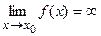, то линия у = f(x) имеет асимптоту х = х₀.

2) Если 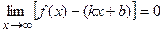, то линия у = f (x) имеет асимптоту у = kx + b, где , .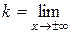

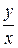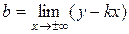Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:

1. Найти область определения функции.

2. Найти асимптоты графика функции.

3. Выяснить, не является ли функция чётной, нечетной или периодической.

4. Найти точки экстремума и интервалы возрастания и убывания

функции.

5. Найти точки перегиба графика функции и интервалы его выпуклости

вверх и вниз.

6. Найти точки пересечения графика функции с осями координат.

7. Построить график функции, используя все полученные результаты

исследования. Если их окажется недостаточно, то следует найти ещё несколько точек графика функции, исходя из её уравнения.

Пример 33. Исследовать функцию и построить её график:

y = .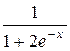

!Ñ В экономике его используют для определения тенденции роста производства предметов потребления.

Решение:

1. Эта функция определена на всей числовой оси.

2. Вертикальных асимптот графика функции нет. Находим наклонные асимптоты:

= ; .

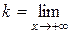
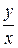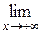
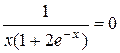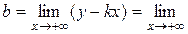
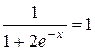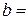
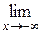
Следовательно, прямая у = 1 есть горизонтальная асимптота. При х® - ¥ к = 0, 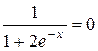, следовательно, у = 0 асимптота при х® - ¥ .

3. Функция не является ни четной, ни нечетной, ни периодической.

4. 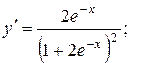производная в ноль ни при каких значениях х не обращается. Следовательно, экстремума нет. Функция всюду возрастает, так как производная положительна для всех х.

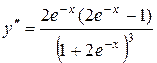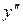5. , = 0 при х = 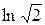. Точка А ( 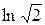; 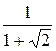) есть точка перегиба, так как вторая производная при переходе через эту точку меняет знак.

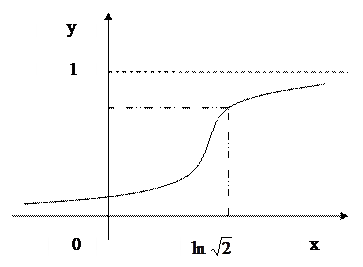
6. График функции не пересекает ось Ох.

7. Используя все полученные данные, строим график функции (рис.11). Рис.11