Взаимное расположение линии второго порядка и прямой

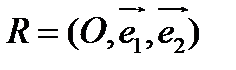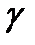Пусть относительно аффинной системы координат линия второго порядка задана уравнением

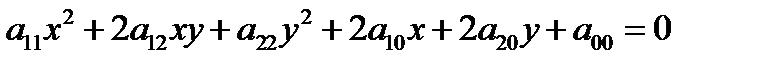(1),

прямая 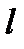задана параметрическими уравнениями

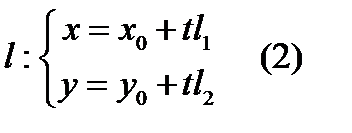
Пересечение прямой и линии второго порядка находится из системы уравнений (1) и (2). Подставляя (2) в (1), получим

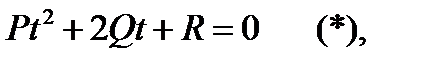
где

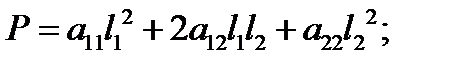
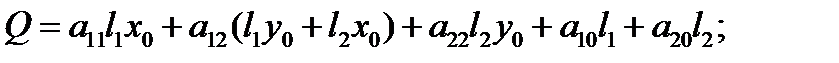
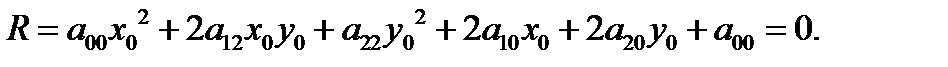
Возможны случаи:

I. , (*) – квадратное уравнение с дискриминантом .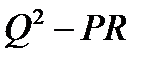

а) 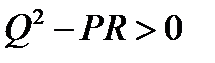. Уравнение (*) имеет два вещественных корня и прямая 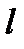пересекает линию 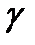в двух вещественных точках .

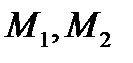б) 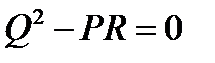. Уравнение (*) имеет два одинаковых корня, прямая пересекает линию второго порядка в двух совпавших точках.

в) 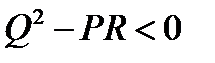. Уравнение (*) имеет два мнимых комплексно сопряженных корня, прямая пересекает линию второго порядка в двух мнимых комплексно сопряженных точках.

II. 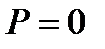, то есть 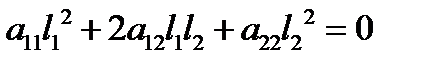. Уравнение (*) принимает вид .

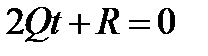а) 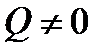. Уравнение (*) имеет единственный корень, прямая пересекает линию второго порядка в одной точке.

б) 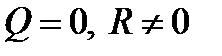. Уравнение (*) не имеет корней, прямая не пересекает линию второго порядка.

в) 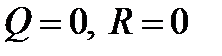. Уравнение (*) становится тождеством, то есть любая точка прямой лежит на линии второго порядка, прямая является частью линии второго порядка.

О п р е д е л е н и е. Направлением на плоскости называется семейство всех параллельных между собой прямых.

Очевидно, что направление вполне определяется направляющим вектором этих прямых.

О п р е д е л е н и е. Направление, определяемое ненулевым вектором, называется асимптотическим направлением относительно линии второго порядка, если любая прямая этого направления имеет с линией второго порядка не более одной общей точки, или является частью этой линии.

Из предыдущих рассуждений получаем, что направление, определяемое ненулевым вектором 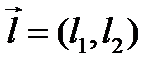, является асимптотическим относительно линии второго порядка тогда и только тогда, когда 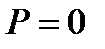. Таким образом, имеем условие асимптотического направления:

.

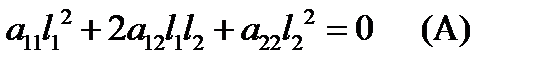Сколько может быть асимптотических направлений относительно линии второго порядка?

Заметим, что для задания направления достаточно знать отношение координат вектора .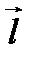

I. 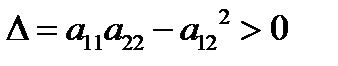. В этом случае 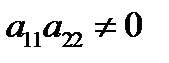и из условия (А) получаем, что 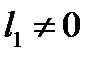(в противном случае получаем, что 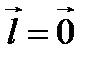). Из уравнения (А) получаем квадратное уравнение относительно 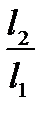, дискриминант которого 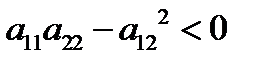. То есть это уравнение не имеет корней, а значит, относительно линии второго порядка нет асимптотических направлений. В этом случае линия называется линией эллиптического типа. Можно проверить, что эллипс, мнимый эллипс, пара мнимых пересекающихся прямых – линии эллиптического типа.

II. .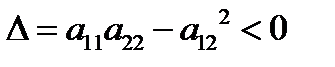

а) 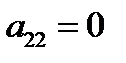. В этом случае (А) принимает вид 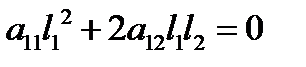. Имеем два асимптотических направления относительно линии второго порядка, определяемые векторам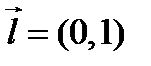и и .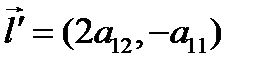

б) 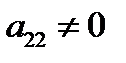. Из уравнения (А) следует, что 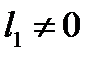. Имеем квадратное уравнение 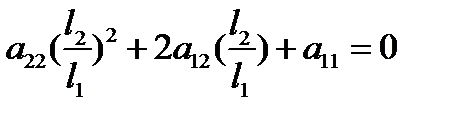, дискриминант которого больше нуля. То есть это уравнение имеет два различных корня, а значит, относительно линии второго порядка существует ровно два асимптотических направления. В этом случае линия называется линией гиперболического типа. Можно проверить, что гипербола, пара пересекающихся прямых – линии гиперболического типа.

III. 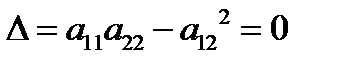. Рассмотрев случаи, когда 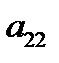равно и не равно нулю, получим, что относительно линии второго порядка существует ровно одно асимптотическое направление. В этом случае линия второго порядка называется линией параболического типа. Убедитесь, что парабола, пара параллельных, пара мнимых параллельных и пара совпавших прямых являются линиями параболического типа.

О п р е д е л е н и е. Прямая называется касательной к линии второго порядка, если она пересекает эту линию в двух совпавших точках.

Из предыдущих рассуждений следует, что прямая, задаваемая уравнением (2), является касательной к линии второго порядка 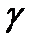, есл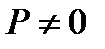и и .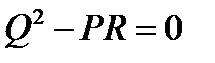

Выбрав точку касания в качестве начальной точки 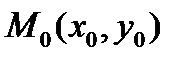для прямой 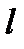, получим 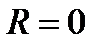. Тогда 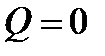, то есть

.

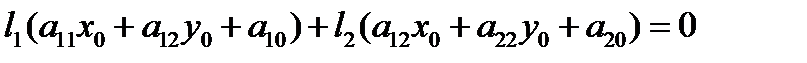И в качестве направляющего вектора касательной можно выбрать вектор с координатами

.

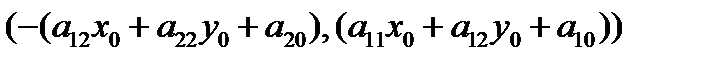Каноническое уравнение касательной в точке 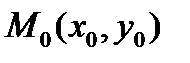линии второго порядка будет иметь вид

.

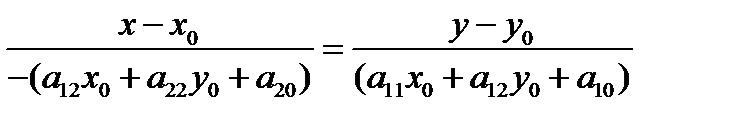У п р а ж н е н и е. Найти уравнение касательной к эллипсу, гиперболе, параболе, заданным каноническими уравнениями.