Прямая на плоскости

Прямая ℓ может быть задана уравнением одного из следующих видов:

1) Ах + Ву + С = 0 – общее уравнение прямой;

2) А (х – х₀) + В (у – у₀) = 0 – уравнение прямой, проходящей через точку М₀ (х₀, у₀) с заданным нормальным вектором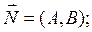

3) 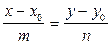– уравнение прямой, проходящей через точку М₀ (х₀, у₀) с заданным направляющим вектором 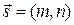(каноническое уравнение);

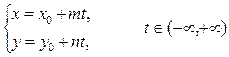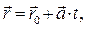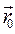4) – параметрические уравнения прямой, которые в векторной форме имеют вид где – радиус-вектор точки М₀, 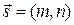– направляющий вектор прямой;

5) у – у₀ = k (х – х₀) или y = kx + b – уравнение прямой с угловым коэффициентом k, где k = tg α

Угол между двумя прямыми.Если прямые ℓ₁, ℓ₂ заданы следующими уравнениями:

ℓ₁: А₁х + В₁у + С₁ = 0,

ℓ₂: А₂х + В₂у + С₂ = 0,

то угол между прямыми (один из смежных углов) – это угол между нормальными векторами этих прямых. Следовательно,

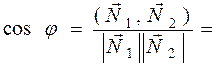
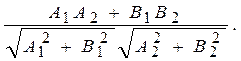
Если прямые ℓ₁ и ℓ₂ заданы уравнениями с угловым коэффициентом

ℓ₁: у = k₁х + b₁ ,

ℓ₂: y = k₂х + b₂,

то угол φ между прямыми находится по формуле

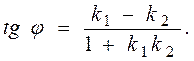
Пример 14. В треугольнике АВС известны вершины А (2,-2), В (-1,1), С(1,4). Составить: уравнение стороны ВС; уравнение высоты АН; уравнение медианы АD.

Решение:

1. Для составления уравнения стороны ВС воспользуемся

уравнением прямой, проходящей через две точки:

.

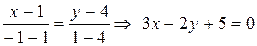Отсюда, в частности, следует, что k_BC = 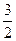, где k_BC - угловой коэффициент прямой ВС.

2. Так как высота АН перпендикулярна стороне ВС, то

k_AH = 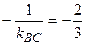. Далее, точка А (2,-2) лежит на высоте АН. Следовательно, уравнение высоты АН вытекает из уравнения прямой, проходящей через точку с угловым коэффициентом, тогда имеем: у+2 = -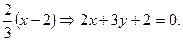

3. Так как АD – медиана треугольника АВС, то точка В делит сторону ВС пополам. Следовательно, координаты точки D равны полусумме координат точек В и С, то есть D =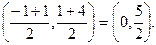

Теперь для составления уравнений медианы АD мы можем воспользоваться уравнением прямой, проходящей через две заданные точки:

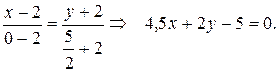
4.2. Плоскость и прямая в пространстве

Плоскость Р в декартовой прямоугольной системе координат Охуz может быть задана уравнением одного из следующих видов:

1. Ах + Ву + Сz + D = 0 – общее уравнение плоскости.

2. Ненулевой вектор N, перпендикулярный плоскости, называют ее нормальным вектором.

А (х – х₀) + В (у – у₀) + С (z – z₀) = 0 – уравнение плоскости, проходящей через точку М₀ (х₀, у₀, z₀) перпендикулярно нормальному вектору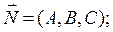

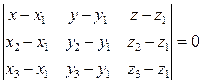3. – уравнение плоскости, проходящей через три точки М₁ (х₁, у₁, z₁), М₂ (х₂, у₂, z₂), М₃ (х₃, у₃, z₃).

Угол между плоскостями.Если плоскости Р₁ и Р₂ заданы уравнениями

Р₁: А₁х + В₁у + С₁z + D₁ = 0,

Р₂: А₂х + В₂у + С₂z + D₂ = 0,

то угол φ между плоскостями (один из двух двугранных углов) и угол между нормальными векторами этих плоскостей

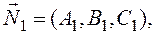
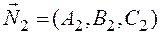
определяется по формуле

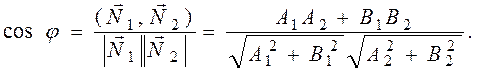
Расстояние от точки до плоскости.

Пусть δ – расстояние от точки М^* (х^*, у^*) до плоскости

Р: Ах + Ву + Сz + D = 0. Тогда

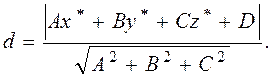
Уравнения прямой в пространстве. 1. Прямая L в пространстве может быть задана общими уравнениямикак пересечение двух непараллельных плоскостей:

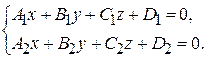
2. Каноническое уравнение прямой, проходящей через точку М₀ (х₀, у₀, z₀) с заданным направляющим вектором :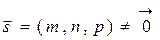

.

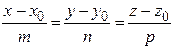3. Уравнение прямой, проходящей через две заданные точки

М₁(х₁, у₁, z₁) и М₂(х₂, у₂, z₂):

.

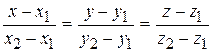4. Параметрические уравнения: .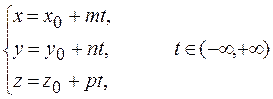

5. Параметрическое уравнение прямой в векторной форм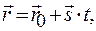е где 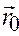– радиус-вектор точки М₀, 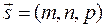– направляющий вектор прямой.

Переход от общих уравнений к каноническим.Пусть прямая L задана общими уравнениями:

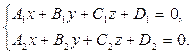
Тогда в качестве направляющего вектора прямой L можно взять вектор

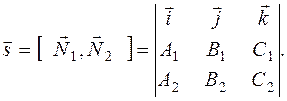
Угол между двумя прямыми.Пусть в пространстве даны две прямые:

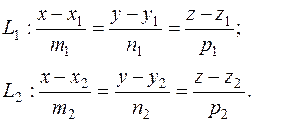
Под углом между двумя прямыми понимают один из двух смежных углов, которые образуют прямые, проведенные параллельно данным через какую-либо точку пространства. Этот угол равен углу φ между направляющими векторами 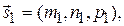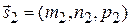данных прямых:

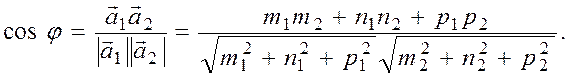
Угол между прямой и плоскостью. Пусть в пространстве даны прямая и плоскость:

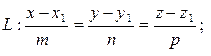
Р: Ах + Ву + Сz + D = 0.

Тогда угол между прямой и плоскостью вычисляется по формуле

sin 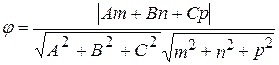. (11)

Взаимное расположение прямой и плоскости в пространстве. Даны

прямая L и плоскость Р уравнениями:

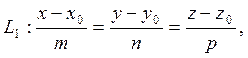Р: Ах + Ву + Сz + D = 0.

Прямая и плоскость параллельны, если направляющий вектор sперпендикулярен нормальному вектору N (рис.1):

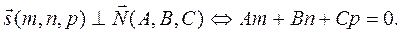
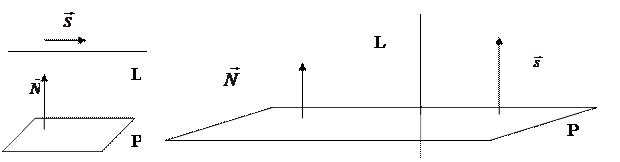
Рис. 1

Прямая и плоскость перпендикулярны, если направляющий вектор sколлинеарен нормальному вектору N:

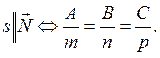
Пример 15.Даны координаты вершин пирамиды АВСД:

А(0;-1;2), B(1;-2;3), C(-1;2;-1), Д(4;1;2). Найти:

а) уравнение плоскости 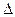ABC;

б) уравнение высоты ДO пирамиды, длину высоты ДO;

в) угол между ребром AД и гранью ABC.

Решение:

1. Находим векторы: АВ = = ;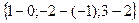

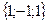АС = .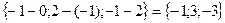

Составим уравнение плоскости АВС, проходящей через три точки А,В,С. Пусть точка М(x,y,z) принадлежит искомой плоскости, тогда векторы АМ(х-0;у+1;z-2), АВ(1;-1;1), АС(-1;3;-3) компланарны.

Следовательно, (АМ, АВ, АС)=0 или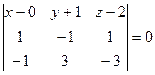

Разложим определитель по элементам первой строки:

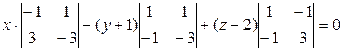или 2(у +1) + 2(z -2) = 0,

где у + z -1 = 0 - уравнение искомой плоскости, откуда N(0;1;1;) - вектор, перпендикулярный искомой плоскости.

2. Так как ДО - высота, то направленный вектор прямой ДО вектор S₁коллинеарен вектору N (0;1;1).

Уравнение прямой, проходящей через точку с направляющим вектором S(m,n,p), имеет вид = = ,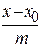

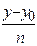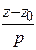поэтому уравнение ДО выглядит так: = = .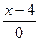

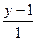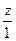Длину высоты ДО находим по формуле (9):

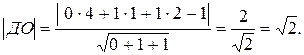
3. Угол между ребром АД и плоскостью АВС вычисляется по формуле (11), составим уравнение прямой АД: 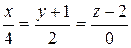, тогда sin ,

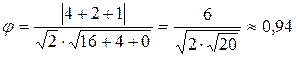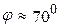
Пример 16. Даны три точки: А(0,-1,1), В(-2,3,2), С(1,1,-1). Составить уравнение плоскостей, проходящих:

1) через точку А перпендикулярно вектору ;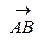

2) проходящей через три точки А,В,С.

Решение:

1.Уравнение плоскости Р получится как условие перпендикулярности векторов:

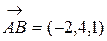и 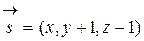. Так как 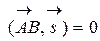, то

-2 ( х – 3 ) + 4(у +1) + (z – 1) = 0 -2x + 4y + z + 9 = 0.

2. Найдем уравнение плоскости, проходящей через точки А, В, С. Введем произвольную точку М(х,y,z) плоскости Р и вычислим вектор

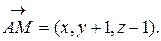
Векторы 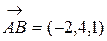и 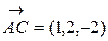являются базисными векторами плоскости Р. Уравнение плоскости Р получится как условие линейной зависимости трех векторов:

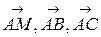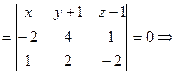( ) -10x-3y-8z+5=0.

Пример 17. Найти точку пересечения прямой

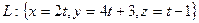и плоскости Р : х+2y+3z+10 =0.

Решение. Нужно совместно решить их уравнения

.

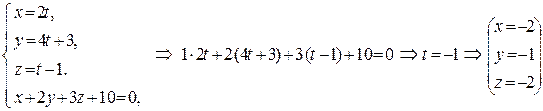Таким образом, искомая точка М(-2,-1,-2).

<2 3 456 7 8 >

Дата добавления: 2020-07-18; просмотров: 474;

Поиск по сайту

Узнать еще