Теорема о дополняющей нежесткости
Для того чтобы допустимые Z,U были оптимальными, необходимо и достаточно выполнение условия
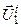
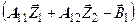 =0 и
=0 и 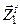
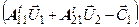 =0.
=0.
Это означает, что в точке оптимума никогда не может одновременно быть так, чтобы
i-я компонента вектора переменных основной задачи была положительна, а i-е неравенство двойственной задачи выполнялось строго (неравенства приобретают форму равенств). Если известно оптимальное решение 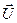 двойственной задачи, то, подставив его в приведенные выражения, получим два линейных уравнения для
двойственной задачи, то, подставив его в приведенные выражения, получим два линейных уравнения для 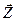 . Вместе с
. Вместе с 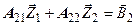 они составляют систему уравнений, из которой можно определить решение поставленной задачи.
они составляют систему уравнений, из которой можно определить решение поставленной задачи.
Исходный пример. Пусть требуется решить задачу линейного программирования (8.22),(8.23).
Рассмотрим ДЗЛП, которая является СЗЛП
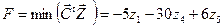
при ограничениях
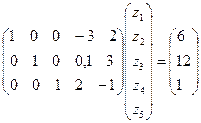 ,
,
zi ≥ 0.
Эта СЗЛП была рассмотрена ранее (п.8.4). В результате ее решения получены решения z2 = z3 = 0 (внебазисные переменные), z1 = 5,541; z4 = 3,918; z5 = 2,459 (базис). Ф=СХ=-77,9672. Отсюда уравнения 1,4,5в(8.23). приобретают форму равенств, а 2,3 – строгих неравенств. Решение определяется из системы уравнений.
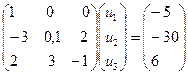 .
.
В результате 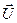 =(-5; -2,13; -22,39)t. F=
=(-5; -2,13; -22,39)t. F= 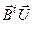 =-77,97=
=-77,97= 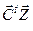 .
.
Дата добавления: 2020-07-18; просмотров: 593;











