Двойственная задача линейного программирования
Пусть требуется решить задачу линейного программирования.
max( 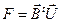 =6u1+12 u2+u3) =6u1+12 u2+u3)
| (8.22) |
при условии
| u1£-5; u2£0; u3£0; -3 u1+0,1 u2+2 u3£-30; 2 u1+3 u2- u3£6; ui – любое. | (8.23) |
Как решать? И, прежде всего в условиях, когда переменные принимают произвольные значения? Одним из путей является введение дополнительных переменных vj, vn+j ≥0, j=1,…, n для замены исходных переменных uj = vj - vn+j и представления задачи к виду СЗЛП. Кроме того, требуется ввести новые переменные для преобразования неравенств в равенства Размерность задачи, а следовательно, и длительность расчетов резко возрастают.
Другим подходом является решение исходной ЗЛП через так называемую двойственную задачу линейного программирования (ДЗЛП).
Двойственностьв математическом программировании (МП), как и вообще в математике, играет фундаментальную роль. Она выступает в качестве краеугольного камня соответствующих теорий, порождает арсенал конструктивных средств анализа математических моделей, построения эффективных алгоритмов решения задач и формальной оценки этой эффективности.
Если 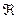
 - некоторый исходный математический объект (модель), то двойственный объект
- некоторый исходный математический объект (модель), то двойственный объект 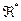 , вообще говоря, выступает как некий внешний по отношению к
, вообще говоря, выступает как некий внешний по отношению к 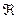 объект ''наблюдения'' за
объект ''наблюдения'' за 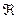 . Содержание двойственности в МП состоит в сопоставлении исходной задаче
. Содержание двойственности в МП состоит в сопоставлении исходной задаче 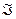 другой задачи
другой задачи 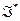 , формируемой по определенным правилам и называемой двойственной. Эти задачи связаны математически содержательными соотношениями, позволяющими, например, получить оценки критериальной эффективности всех параметров, формирующих основную задачу; свести решение основной оптимизационной задачи к решению некоторой системы неравенств; сформировать в изящной форме условия оптимальности и т.д.
, формируемой по определенным правилам и называемой двойственной. Эти задачи связаны математически содержательными соотношениями, позволяющими, например, получить оценки критериальной эффективности всех параметров, формирующих основную задачу; свести решение основной оптимизационной задачи к решению некоторой системы неравенств; сформировать в изящной форме условия оптимальности и т.д.
Если задача МП (или ЛП) - результат моделирования конкретной экономической (производственной) ситуации, то двойственность и та информация, которую двойственность порождает, позволяют провести глубокий анализ (экономико-математический анализ) моделируемого объекта, выявить узкие места, тенденции динамики объекта, выразив эти факторы в количественной форме. Профессионально сделанные пакеты прикладных программ, решающие задачи МП или ЛП, обычно выдают в форме удобных распечаток всю совокупность информации, необходимую для экономико-математического анализа.
Теорема о двойственности: Каждой ЗЛП можно сопоставить точно одну двойственную ей (ДЗЛП) и решение одной из задач определяет решение другой.
Исходная ЗЛП является двойственной по отношению к ДЗЛП, т.е. понятие двойственности является симметричным
Структуру двойственной задачи линейного программирования лучше всего видеть на примере симметричной ДЗЛП.
| ЗЛП | ДЗЛП | |
| Функционал | Min( 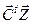 ) )
| Max( 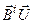 ) )
|
| Ограничения | 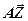 ≥ ≥ 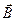 (m уравнений) (m уравнений)
| 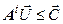 ; (n уравнений) ; (n уравнений)
|
| Переменные | 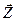 ³0 (n переменных) ³0 (n переменных)
| 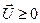 (m переменных) (m переменных)
|
В ЗЛП столько переменных, сколько неравенств среди ограничений в ДЗЛП и столько ограничений, сколько переменных в ДЗЛП, каждому ограничению одной задачи соответствует переменная другой. Сравнивая структуры нетрудно видеть, что вектора 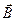 и
и 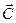 поменялись местами. Матрица А в системе ограничений транспонировалась, знаки неравенств поменялись на противоположные, а функция min() преобразовалась в max().
поменялись местами. Матрица А в системе ограничений транспонировалась, знаки неравенств поменялись на противоположные, а функция min() преобразовалась в max().
В более общем виде, при наличии ограничений типа «равенство» связь задач задается следующим образом:
| ЗЛП | ДЗЛП | |
| Функционал | Min( 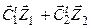 ) )
| Max 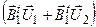
|
| Ограничения | 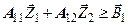 ..(k уравнений) ..(k уравнений)
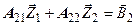 ; (m уравнений) ; (m уравнений)
| 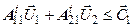 ; (n уравнений) ; (n уравнений)
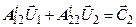 ; (r уравнений) ; (r уравнений)
|
| Переменные | 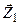 ³0 (n переменных) ³0 (n переменных)
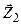 – любое (r переменных) – любое (r переменных)
| 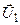 ³0 (k переменных) ³0 (k переменных)
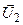 - любое (m переменных) - любое (m переменных)
|
Структурную взаимосвязь переменных и ограничений можно представить в не совсем строгом, но понятном для восприятия виде. Исходная ЗЛП может быть представлена следующей матричной структурой:
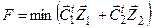
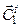
| 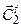
| ||||
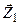 ³0 ³0
| 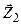 - любое - любое
| ||||
| Размерность | n | r | Θ | ||
| k | A11 | A12 | 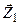
| ≥ | 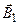
|
| m | A21 | A22 | 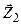
| = | 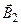
|
Транспонированием структуры относительно матрицы ограничений и заменой переменных получаем структуру двойственной задачи ЛП.
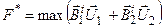
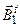
| 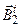
| ||||
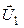
| 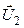 - любое - любое
| ||||
| Размерность | k | m | Θ | ||
| n | At11 | At21 | 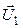
| ≤ | 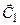
|
| r | At12 | At22 | 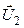
| = | 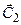
|
Согласно теореме двойственности если разрешима одна задача, то разрешима и другая; оптимальные значения целевых функций при этом одинаковы
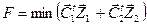 =
= 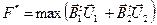
Для получения решения исходной задачи ЛП при известном решении двойственной необходимо принять во внимание, что если j-я компонента вектора переменных ДЗЛПне равна нулю, тоj-е уравнение системы ограничений основной ЗЛП обращается встрогое равенство, (ЗЛП является двойственной по отношению к ДЗЛП). Как правило, полученная система уравнений является достаточной для определения решения основной ЗЛП. Дополнительными (если это потребуется) к полученной системе уравнений являются уравнения
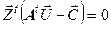 ;
; 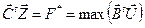 ,
,
которые и отражают описанные выше соотношения: ограничение - равенство (скобка равна нулю) – соответствующая двойственная переменная не равна нулю и наоборот, а также равенство оптимальных целевых функций основной и двойственной задач ЛП .
Дата добавления: 2020-07-18; просмотров: 656;











