Геометрическая интерпретация решения СЗЛП

Для системы из m уравнений с n неизвестными существует бесконечное множество решений, зависящее от r = n – m параметров. Любой элемент такого множества может быть представлен точкой в пространстве независимых переменных. Для рассмотренного примера пространство независимых переменных представляет собой плоскость с осями координат 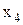и . Область допустимых значений задачи ЛП ограничивается требованиями неотрицательности всех переменных, в том числе и независимых 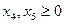. Отсюда ОДЗ ограничивается первым квадрантом плоскости .

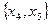Условие неотрицательности зависимых переменных может быть представлено выбором полуплоскоси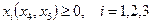

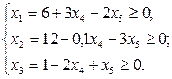
Для идентификации полуплоскостей целесообразно проанализировать, в какой области лежит точка 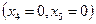. Так для первого уравнения точке 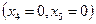соответствует 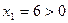. Отсюда эта точка лежит в допустимой области.

Если построен начальный базис (как в нашем случае), то точка, где независимые переменные равны нулю должна удовлетворять ОДЗ. Отсюда точка 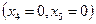принадлежит области 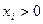и нет надобности проверять знак функций 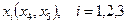в этой точке.

В силу линейности целевой функции ее градиент 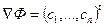(антиградиент) одинаков в любой точке ОДЗ. Отсюда решение СЗЛП является наиболее удаленная в направлении антиградиента точка ОДЗ (на ее границе). Как правило, это вершина выпуклого многогранника ОДЗ. Отсюда решение может быть найдено путем анализа лишь оболочки ОДЗ (вершин и граней).

В многомерной геометрии точку пересечения r плоскостей 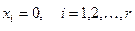вместе с выходящими из этой точки лучами 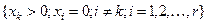называют симплексом порядка r. Этим и объясняется название базового метода решения СЗЛП– симплекс-метод.

Ф=-10

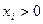В результате построения подобластей формируется многоугольник (ABCDE на рис. 8.4) , все внутренние точки которого представляют собой допустимые сочетания зависимых переменных.

В рассматриваемом примере m = 3, n = 5. Отсюда максимальное число базисных решений

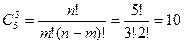
Однако допустимых (удовлетворяющих условию 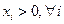) базисных решений только 5 (5 базисных решений являются недопустимыми, например вершина, соответствующая х₁=0, х₅=0. поскольку здесь х₄<0).Именно допустимые базисные решения образуют множество вершин многогранника ОДЗ.

Как было отмечено, направлением движения к оптимальному решению является антиградиент 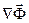целевой функции. Воспользуемся выражением целевой функции через независимые переменные 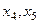: 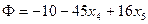. Антиградиент

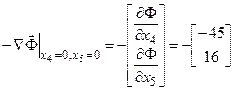
перпендикулярен линии равного уровня 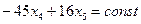. Наиболее удаленная в направлении антиградиента вершина многогранника ABCDE это точка D (х₂=0, х₃=0), которая и является решением СЗЛП.

Однако алгоритмически движение не может осуществляться строго по направлению антиградиента, поскольку в этом направлении возможен выход за пределы ОДЗ. В симплекс-алгоритме движение осуществляется только по ребрам многогранника. При этом на каждом шаге выбирается ребро, наиболее близкое к антиградиенту (наименьший по модулю острый угол между направлениями ребра и антиградиента).

Шаг оканчивается в следующей вершине, служащей основанием нового симплекса. Наконец в точке 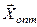угол, образуемый каждым из ребер симплекса с антиградиентом, оказывается тупым, что и свидетельствует о невозможности дальнейшего уменьшения целевой функции.

В рассматриваемом примере движение из начальной вершины А осуществляется по ребру АЕ (х₅=0, х₄=var) до пересечения с линией х₃=0 (вершина Е), где производится замена базиса (х₄ 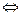х₃). Далее движение выполняется по ребру ED (х₅=var, х₃=0) до пересечения в точке D с линией х₂=0. Далее движенне не возможно, поскольку нет ребра, образующего острый угол с направлением антиградиента.