Приведение задачи к стандартной форме

Общая форма задачи линейного программирования отличается от стандартной наличием уравнений типа неравенств:

.

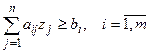(8.20)

Путем введения новой переменной

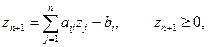
рассматриваемое неравенство преобразуется к виду

.

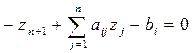Выполняя данную операцию для всех неравенств, получаем задачу линейного программирования стандартного вида.

Неравенства 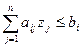преобразуются к виду (8.20) умножением левой и правой части на (-1).

Преобразование простых ограничений .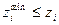

Здесь вводится новая переменная 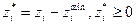. Путем замены 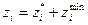в целевой функции и уравнениях ОДЗ задача приводится к стандартному виду.

Ограничения 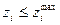приводятся к стандартному виду путем замены переменных .

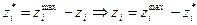Двухсторонние ограничения 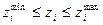не удается разрешить простой заменой одной переменной. Здесь возможен следующий подход. Выполняется замена переменной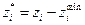 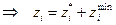, 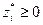. В систему ограничений ОДЗ вводится дополнительное неравенство: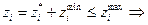 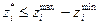. В частности, при 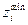=0 достаточно лишь одного дополнительного неравенства в ОДЗ .

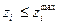В случае, когда переменная принимает произвольные (как положительные, так и отрицательные) значения возможна ее замена 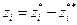двумя новыми, не отрицательными переменными

7.7. Получение начального плана

Симплекс–метод начинает работать, когда найдено начальное базисное решение задачи, т.е. переменные разделены на зависимые и независимые, а все составляющие базиса неотрицательны. Однако не всегда просто удается выполнить эти условия, особенно последние.

Так в системе ограничений типа равенств

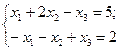
затруднительно записать начальное допустимое базисное решение. Действительно, если в качестве независимых переменных выбрать 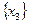, то базис 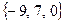является недопустимым.

Начальный допустимый базис можно найти простым перебором базисов, по аналогии с методами решения СЛУ с прямоугольными матрицами коэффициентов (п.4.8), но здесь для каждого вектора независимых переменных совокупность зависимых переменных можно получить лишь построением и решением сопутствующей СЛУ, что связано с большими затратами машинного времению

Другим способом определения начального базиса является решение так называемой «вспомогательной задачи линейного программирования (ВЗЛП)», основная идея которой заключается в том, что по числу уравнений-ограничений вводятся вспомогательные переменные, которые будут зависимыми, а все исходные переменные - независимыми. Формируется функционал, определяемый суммой вспомогательных переменных, и выполняется решение СЗЛП. Ее решение тривиально, т.е. все вспомогательные переменные будут равны нулю. Однако в процессе решения будет получен допустимый базис, поскольку в процессе, так и на последнем этапе решения ЗЛП переменные не отрицательны. Этот базис может быть выбран в качестве исходного для решения основной ЗЛП.

В каноническом виде исходная система ограничений записывается в виде:

,

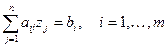где n – число переменных, m – число уравнений.

Предположим, что все значения 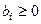. Если у какого-то уравнения 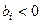, то умножение на (-1) левой и правой частей приводит к положительной правой части.

Добавим к каждому ограничению по одной новой переменной 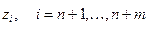, что позволяет сформировать новую систему ограничений:

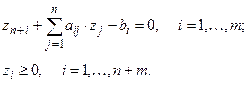
Вспомагательная целевая функция

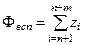, т.е. .

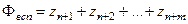В каноническом виде система ограничений ОДЗ имеет вид

,

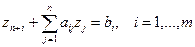(8.21)

или в матричной форме

,

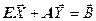где

.

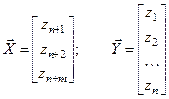Поскольку 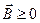, то при 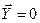все .

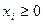В начальном базисном решении значение вспомогательной целевой функции

.

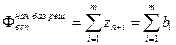Оптимальным решением является .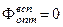

В процессе решения ЗЛП из множества зависимых переменных постепенно удаляются вспомогательные переменные. Если все вспомогательные переменные будут переведены в разряд независимых, то в базисном решении они равны нулю, что соответствует 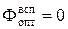. Однако возможны решения, когда 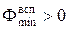. Это означает, что ОДЗ пуста, т.е. система ограничений в исходной задаче линейного программирования противоречива и не имеет решения.