Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребления, имеет решение.
Транспортную задачу можно решить и симплекс-методом, но, внимательно просмотрев математическую модель этой задачи, можно видеть, что существуют некоторые отличительные особенности (матрица ограничений содержит только единицы и нули, все ограничения – равенства), которые позволяют разработать специальные методы, существенно упрощающие процесс вычислений.
Условие задачи можно записать в виде таблицы (табл. 8.3), которую в дальнейшем будем называть матрицей планирования и на базе которой строится алгоритм решения транспортной задачи.
Таблица 8.3
| Постав-щики | Потребители | Запасы | ||||||
| B1 | B2 | Bn | ||||||
| А1 | С11 | С12 | … | С1n | a1 | |||
| x11 | x12 | x1n | ||||||
| А2 | С21 | С22 | … | С2n | a2 | |||
| x21 | x22 | x2n | ||||||
| … | … | … | … | … | … | … | … | … |
| Аm | Сm1 | Сm2 | … | Сmn | am | |||
| xm1 | xm2 | xmn | ||||||
| спрос | b1 | b2 | bn |
7.9.1. Построение первоначального опорного плана
Как и для других задач линейного программирования, итерационный процесс по отысканию оптимального плана транспортной задачи начинают с опорного плана.
Рассмотрим систему ограничений (8.25) и (8.26) транспортной задачи. Она содержит mn неизвестных и m+n уравнений, связанных соотношением (8.27). Если сложить почленно уравнения отдельно подсистемы (8.25) и отдельно подсистемы (8.26), то получим два одинаковых уравнения. Это говорит о линейной зависимости системы уравнений. Если одно из уравнений отбросить, то в общем случае система ограничений будет содержать m+n-1 линейно независимых уравнений, следовательно, невырожденный опорный план транспортной задачи содержит m+n-1 положительных компонент или перевозок.
Таким образом, если каким-либо способом получен опорный план транспортной задачи, то в матрице (хij) (i = 1, 2,...,n ; j = 1, 2, ...,m) его компонент (табл. 8.3) положительными являются не более m+n-1, а остальные равны нулю.
Если условия транспортной задачи и ее опорный план записаны в виде табл. 8.3, то клетки, в которых находятся отличные от нуля перевозки, называются занятыми, остальные - незанятыми. Занятые клетки соответствуют базисным неизвестным, и для невырожденного опорного плана их количество равно
m+n-1. Если ограничения транспортной задачи записаны в виде (8.25) и (8.26), то, как известно, базисным неизвестным, включенным в опорный план, соответствует система линейно независимых векторов.
| Рис. 8.5. Циклы |
Циклы
 Одним из ключевых моментов алгоритмов транспортной задачи является анализ наличия циклов. Циклом называется набор клеток (рис. 8.5) вида
Одним из ключевых моментов алгоритмов транспортной задачи является анализ наличия циклов. Циклом называется набор клеток (рис. 8.5) вида 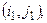
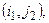
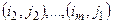 в котором две и только две соседние пары расположены в одном столбце или одной строке таблицы, причем последняя пара находится в той же строке или столбце, что и первая.
в котором две и только две соседние пары расположены в одном столбце или одной строке таблицы, причем последняя пара находится в той же строке или столбце, что и первая.
Понятие цикла обусловлено целесообразностью решения вспомогательной задачи, которая часто определяется как «списание общего долга». Суть такой задачи заключается в следующем. Пусть индивид А должен некоторую сумму индивиду В. В свою очередь индивид В задолжал у С, а С – у А (цикл). Нетрудно сообразить, что общий долг может быть списан со всех участников любителей взять в долг. В результате, один из участников будет без долгов.
Специфика цикла в транспортной задаче заключается в том, что для соблюдения балансовых условий (8.27) необходимо четное число участников обмена, поскольку для сохранения баланса товарооборота в какой-либо внешней группе (потребитель k) если от одного из производителей пришло больше товара, то от другого производителя этому потребителю товара должно придти меньше на такое же количество. Только в этом случае возможно списание общего долга
Построение циклов начинается с какой-либо занятой клетки и выполняется переход по столбцу (строке) к другой занятой клетке, в которой делается поворот под прямым углом и далее движение по строке (столбцу) к следующей занятой клетке и т. д., с целью возвратиться к первоначальной клетке. Если такой возврат возможен, то получен цикл. При этом рассматриваемый план не является опорным (удовлетворяющий всем условиям ОДЗ).
Математическое доказательство последнего утверждения здесь опускается. В то же время на примере цикла из четырех вершин легко доказать, что замкнутый цикл не может отражать опорный план. Действительно, если в двух соседних клетках в одной прибавить, а в другой отнять одно и тоже число и так по всему циклу, то баланс не изменится, но в результате будет получен новый план, что говорит о не единственности решения, а следовательно о линейной зависимости системы уравнений, что противоречит основному допущению базиса.
Опорность плана при записи условий транспортной задачи в виде таблицы заключается в его ацикличности, т.е. в таблице нельзя построить замкнутый цикл, все вершины которого лежат в занятых клетках.
Всякий план транспортной задачи, содержащий более m+n-1занятых клеток, не является опорным, так как ему соответствует линейно зависимая система векторов. При таком подходе в таблице всегда можно построить замкнутый цикл, с помощью которого можно уменьшить число занятых клеток до m+n-1.
Если к занятым клеткам, определяющим опорный невырожденный (следовательно, и ацикличный) план, присоединить какую-либо незанятую клетку, то план становится неопорным, появляется единственный цикл, все вершины которого, за исключением одной, лежат в занятых клетках.
Первоначальный опорный план транспортной задачи как задачи линейного программирования можно построить ранее рассмотренными методами, однако это сопряжено с большими вычислениями. Существует несколько простых схем построения первоначального опорного плана транспортной задачи.
Дата добавления: 2020-07-18; просмотров: 683;











