Ортонормированность базиса
Математические операции в ортонормированном базисе значительно проще за счет того, что скалярное произведение любых двух векторов базиса равно нулю, а длина каждого вектора равна единице. При этом коэффициенты разложения вектора в упомянутом базисе равны проекциям (скалярному произведению) вектора на единичный орт.
Аппарат минимальных расстояний позволяет выполнить ортогонализацию и нормализацию произвольного базиса. Пусть имеется базис 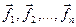 .
.
В качестве первого вектора ортонормированного базиса выбирается вектор 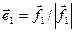 . Вторым вектором является нормированный вектор
. Вторым вектором является нормированный вектор 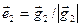 , определяющий минимальное расстояние от
, определяющий минимальное расстояние от 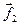 до
до 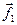 ,
, 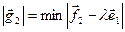 . Подобно (7.5) определяется коэффициент λ. Отсюда вектор
. Подобно (7.5) определяется коэффициент λ. Отсюда вектор 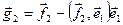 . Аналогично,
. Аналогично, 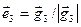 , где
, где 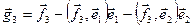 , т.е.
, т.е. 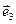 определяется минимальным расстоянием до подпространства, порожденного векторами
определяется минимальным расстоянием до подпространства, порожденного векторами 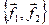 с ортонормированным базисом
с ортонормированным базисом 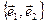 . Распространяя данную процедуру, получаем
. Распространяя данную процедуру, получаем 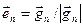 , где
, где 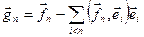 .
.
Очевидно, что если 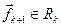 , то
, то 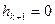 ,
, 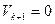 . Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора
. Это замечание делает понятным геометрический смысл особенностей матриц и линейных преобразований с определителем, равным нулю. Если матрица Аимеет определитель, равный нулю, то преобразование, соответствующее матрице А, переводит вектора исходного пространства в вектора подпространства меньшей размерности. В самом деле, поскольку определитель равен по модулю объему параллелепипеда, построенного на образах единичных координатных векторов, то в случае det A = 0 расстояние от конца хотя бы одного вектора 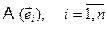 до подпространства предыдущих векторов
до подпространства предыдущих векторов 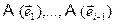 равно нулю. Следовательно,
равно нулю. Следовательно, 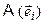 принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства.
принадлежит подпространству i-1векторов. А это в свою очередь означает, что пространство образов имеет уже не n независимых векторов, а меньшее количество и является подпространством исходного пространства.
 Пример. Выполнить ортогонализацию векторов
Пример. Выполнить ортогонализацию векторов 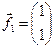
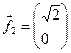 .
.
| Рис. 7.6. Ортогонализация |
Первый вектор нового базиса 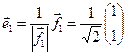 . Перпендикулярный
. Перпендикулярный 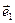 вектор
вектор 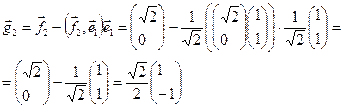 .
.
Второй нормированный вектор нового базиса
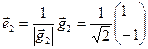 .
.
Новый ортонормированный базис представлен на рис. 7.6.
Дата добавления: 2020-07-18; просмотров: 890;











