Преобразование подобия
Совокупность линейно-независимых собственных векторов образует базис. При этом матрица перехода из исходного базиса в новый представляется совокупностью координат собственных векторов в исходном базисе
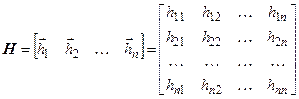 .
.
Соотношения 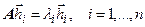 в матричном виде можно представить как
в матричном виде можно представить как
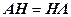 , ,
| (7.8) |
где 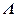 - диагональная матрица из собственных чисел:
- диагональная матрица из собственных чисел: 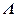 =
= 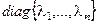 .
.
Нельзя писать 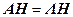 , так как
, так как 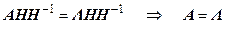 , что не соответствует действительности, и, кроме того, при умножении матрицы H на
, что не соответствует действительности, и, кроме того, при умножении матрицы H на 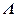 справа действительно, каждый собственный вектор (столбец матрицы H) умножается на соответствующее собственное число
справа действительно, каждый собственный вектор (столбец матрицы H) умножается на соответствующее собственное число
 ,
,
в то время как умножение на диагональную матрицу слева равносильно умножению на коэффициенты 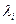 строк, а не столбцов, что противоречит математическому смыслу собственных векторов:
строк, а не столбцов, что противоречит математическому смыслу собственных векторов:
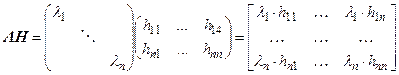 .
.
Умножив уравнение (7.8) сначала справа, а затем слева на матрицу 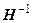 , получим
, получим
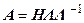 ; ; 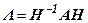 . .
| (7.9) |
МатрицыАи L представляют собой одно и то же линейное преобразование, записанное в различных системах координат. Матрица А показывает преобразование в координатах базиса 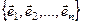 , а матрица L показывает тоже преобразование в координатах базиса
, а матрица L показывает тоже преобразование в координатах базиса 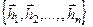 .
.
Итак, одному и тому же линейному преобразованию в разных базисах соответствует отличающиеся матрицы.
Базис1: 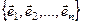 – A,
– A, 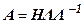 ,
, 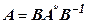
Базис 2: 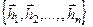 - L ,
- L , 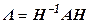
Базис 3: 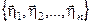 –
– 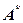 ,
, 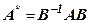 ,
,
где B= 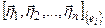 , (см.п.7.2)
, (см.п.7.2)
Матрицы А и L называются подобными, т.к. соответствуют одному и тому же преобразованию. Определители этих матриц равны. Отсюда определитель матрицы равен произведению всех его собственных чисел
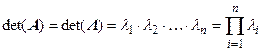 .
.
 Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса
Структурная диаграмма преобразования векторов представлена на рис. 7.9. В частности, если требуется преобразовать вектор из базиса 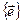 в базис
в базис 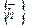 , то необходимо умножить его на матрицу H-1.
, то необходимо умножить его на матрицу H-1.
| Рис. 7.9. Преобразование векторов |
С помощью данной диаграммы легко получается соотношение подобия (7.9), которое показывает переход от вектора 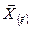 к его образу
к его образу 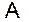
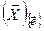 по и против часовой стрелки.
по и против часовой стрелки.
Норма матрицы
Первое (максимальное) собственное число 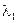 характеризует максимальное растяжение (при
характеризует максимальное растяжение (при 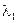 >1) или минимальное сжатие (при
>1) или минимальное сжатие (при 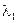 <1) вектора. Поскольку вычисления собственных чисел для матрицы большой размерности представляют значительные трудности, на практике часто используют оценку
<1) вектора. Поскольку вычисления собственных чисел для матрицы большой размерности представляют значительные трудности, на практике часто используют оценку 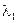 числовой характеристикой матрицы, называемой нормой матрицы
числовой характеристикой матрицы, называемой нормой матрицы 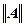 ,
, 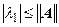 .
.
Норма матрицы является одной из характеристик матрицы. Поскольку матрица является отражением некоторого линейного преобразования, то неудивительно, что норма матрицы теоретически определяется через линейное преобразование верхней границей изменения длины вектора (представленный ниже оператор sup обозначает точную верхнюю границу)
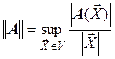 ,
,
т.е. норма матрицы характеризуется максимальным по модулю образом единичного вектора. Отсюда понятно соотношение 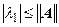 .
.
Используются три способа вычисления нормы матрицы.
1. Кубическая норма (норма по строкам) равна максимальной сумме модулей элементов строк 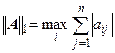 ,.
,.
2. Октаэдрическая норма (норма по столбцам) равна максимальной сумме модулей элементов столбцов, 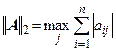 .
.
3. Сферическая норма (Евклидова норма). 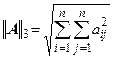 .
.
Свойства норм матрицы:
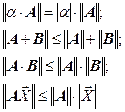
Для любой симметричной матрицы 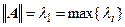 .
.
Дата добавления: 2020-07-18; просмотров: 667;











