Собственные числа и собственные вектора
Для анализа внутренней структуры линейного преобразования целесообразно найти вектора, которые данное преобразование изменяет наиболее просто. Таким свойством обладают собственные вектора матрицы, удовлетворяющие соотношению
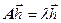 ,
,
где l - коэффициент, показывающий изменения длины вектора, т.е. образ вектора совпадает с прообразом по направлению и отличается от него лишь длиной.
Умножим представленное соотношение слева на единичную матрицу E и перенесем все члены в левую часть.
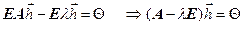
Матрица 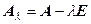 называется характеристической матрицей. Очевидно, что она имеет вид:
называется характеристической матрицей. Очевидно, что она имеет вид:
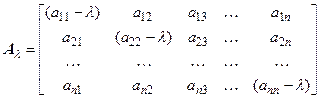
Для вычисления вектора 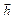 нужно решить систему
нужно решить систему 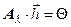 . Эта система однородна (в правой части стоит нулевой вектор) и имеет ненулевое решение
. Эта система однородна (в правой части стоит нулевой вектор) и имеет ненулевое решение 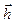 только тогда, когда определитель матрицы
только тогда, когда определитель матрицы 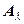 равен нулю (
равен нулю ( 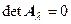 ). В этом случае в матрице
). В этом случае в матрице 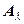 есть линейно зависимая строка, а в системе уравнений – линейно-зависимое уравнение. Удалив это уравнение и задав произвольное значение одной из координат вектора
есть линейно зависимая строка, а в системе уравнений – линейно-зависимое уравнение. Удалив это уравнение и задав произвольное значение одной из координат вектора 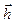 , решением оставшейся части системы можно найти остальные координаты
, решением оставшейся части системы можно найти остальные координаты 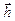 .
.
Для того чтобы найти значение числа l, при котором определитель 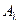 обратился в ноль, нужно аналитически выписать определитель матрицы, приводя подобные члены относительно степеней l. В общем случае для матрицы размерностью nполучим характеристическое уравнение степени n:
обратился в ноль, нужно аналитически выписать определитель матрицы, приводя подобные члены относительно степеней l. В общем случае для матрицы размерностью nполучим характеристическое уравнение степени n:
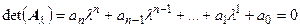 .
.
Известно, что решением уравнения степени nявляется n значений 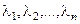 . Числа li называются собственными числами (значениями) матрицы. Обычно li располагают в ряд по уменьшению модуля, при этом максимальное значение обозначают через l1 , а минимальное через ln .
. Числа li называются собственными числами (значениями) матрицы. Обычно li располагают в ряд по уменьшению модуля, при этом максимальное значение обозначают через l1 , а минимальное через ln .
Пусть в качестве базиса принята совокупность собственных векторов 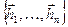 и вектор
и вектор 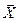 имеет в этой системе координаты
имеет в этой системе координаты 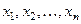 ,
, 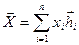 . Тогда
. Тогда 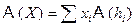 . Поскольку
. Поскольку 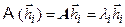 то
то 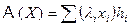 , т.е. при линейном преобразовании координаты вектора по величине сокращаются (li < 1) или удлиняются (li > 1) пропорционально собственным числам. Линейное преобразование
, т.е. при линейном преобразовании координаты вектора по величине сокращаются (li < 1) или удлиняются (li > 1) пропорционально собственным числам. Линейное преобразование 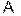 в базисе собственных векторов
в базисе собственных векторов 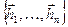 имеет диагональную матрицу
имеет диагональную матрицу
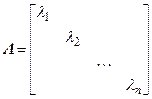 .
.
Если собственные числа li различны, то собственные вектора 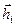 линейно-независимы. Отметим, что если
линейно-независимы. Отметим, что если 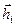 является собственным вектором, то любой вектор
является собственным вектором, то любой вектор 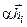 также будет собственным вектором, т.е. для каждого li имеется не один собственный вектор, а бесчисленное множество векторов, лежащих на одном и том же направлении.
также будет собственным вектором, т.е. для каждого li имеется не один собственный вектор, а бесчисленное множество векторов, лежащих на одном и том же направлении.
Таким образом, в базисе из линейно-независимых собственных векторов матрица линейного преобразования преобразует вектор путем растяжения, сжатия или разворота (l<0) координат вектора (умножение проекций на соответствующие собственные числа).
Пример: Найти собственные числа и собственные вектора матрицы 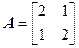 .
.
Характеристическая матрица 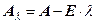 имеет вид
имеет вид
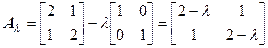
Приравнивая нулю определитель матрицы 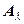 , получим характеристическое уравнение, из которого можно найти собственные числа
, получим характеристическое уравнение, из которого можно найти собственные числа
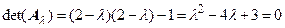 . Отсюда
. Отсюда  .
.
Вычисление собственных векторов. Первый собственный вектор 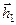 может быть найден из уравнения
может быть найден из уравнения 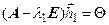 , или
, или
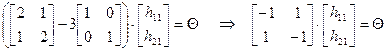 .
.
Последнее матричное уравнение эквивалентно системе:
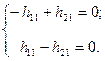 .
.
Нетрудно видеть, что уравнения линейно-зависимы, следовательно, любое из них, например второе, можно удалить. Тогда 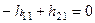 . Задавая
. Задавая 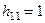 , получим
, получим 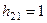 . Отсюда вектор
. Отсюда вектор 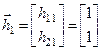 .
.
 Уравнение
Уравнение 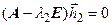 для второго собственного вектора приводит к системе:
для второго собственного вектора приводит к системе: 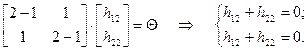
Отбрасываем второе уравнение, задав 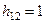 , получим
, получим 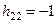 , т.е.
, т.е. 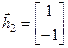 .
.
| Рис. 7.7 |
Найденные вектора представлены на рис. 7.7.
Т.к. матрица А симметрична, то исходный ортонормированный базис преобразуется в ортогональный (можно сделать ортонормированным, поделив каждый вектор нового базиса на его длину).
Рассмотрим некоторый вектор 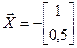 и найдем его образ
и найдем его образ 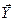 под действием матрицы
под действием матрицы 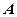 :
:
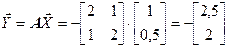
В результате получаем вектор большей длины, расположенный под углом с исходным вектором 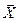 (рис. 7.8).
(рис. 7.8).
Тот же вектор 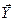 можно получить другим способом. Найдем проекции (OB, CB) вектора
можно получить другим способом. Найдем проекции (OB, CB) вектора 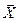 на собственные вектора
на собственные вектора 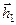 и
и 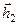 (числа a и b). Линейное преобразование заключается в умножении первой проекции (a) на первое собственное число
(числа a и b). Линейное преобразование заключается в умножении первой проекции (a) на первое собственное число 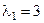 , и второй проекции
, и второй проекции 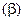 на величину
на величину 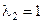 . Геометрически складывая преобразованные проекции (OD и DE), получаем тот же вектор
. Геометрически складывая преобразованные проекции (OD и DE), получаем тот же вектор 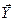 . Аналогично преобразуется любой иной вектор, лежащий на плоскости
. Аналогично преобразуется любой иной вектор, лежащий на плоскости 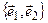 .
.
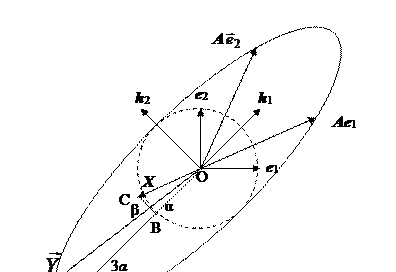

| Рис. 7.8. Линейное преобразование в координатах собственных векторов |
Если взять множество векторов, лежащих концами на единичной окружности, то матрица линейного преобразования будет в 3 раза вытягивать проекции на вектор 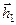 и оставлять неизменными (l2 = 1) проекции на
и оставлять неизменными (l2 = 1) проекции на 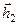 . В результате окружность растягивается в эллипс. Таким образом, собственные числа и собственные вектора дают характеристику преобразования исходного пространства векторов.
. В результате окружность растягивается в эллипс. Таким образом, собственные числа и собственные вектора дают характеристику преобразования исходного пространства векторов.
Дата добавления: 2020-07-18; просмотров: 606;











