Преобразование координат при изменении базиса
Рассмотрим произвольный вектор 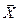 . Его координаты в разных базисах безусловно отличаются
. Его координаты в разных базисах безусловно отличаются
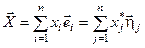 .
.
Вектор 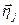 представим через базис
представим через базис 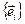 :
: 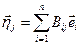 . Отсюда
. Отсюда 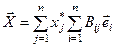 .
.
Выполним замену очередности суммирования 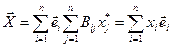 .
.
Отсюда
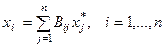
или
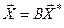 ; ;
| (7.2 ) |
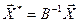 , ,
| (7.3 ) |
где матрица В – матрица базиса 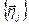 в координатах базиса
в координатах базиса 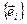 .
.
Пример. Пусть в базисе 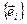
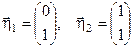 . Вектор
. Вектор 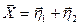 представлен через базис
представлен через базис 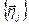 . Определить представление этого вектора в базисе
. Определить представление этого вектора в базисе 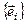 .
. 
Решение.Матрица перехода из базиса 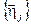 в базис
в базис 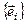 имеет вид
имеет вид 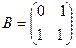 . Отсюда
. Отсюда
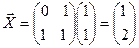 , т.е.
, т.е. 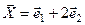 .
.
| Рис. 7.3. Преобразование координат |
То же самое можно получить иначе, через подста новку представлений векторов 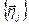 в базисе
в базисе 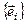
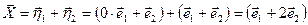 .
.
Геометрический смысл определителя матрицы
В данном разделе ставится задача доказать, что определитель квадратной матрицы А, размерностью 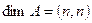 равен по модулю объему n – мерного параллелепипеда, построенного на столбцах матрицы как на векторах
равен по модулю объему n – мерного параллелепипеда, построенного на столбцах матрицы как на векторах 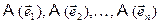 исходного пространства Rn, т.е. построенного на образах базисных векторов.
исходного пространства Rn, т.е. построенного на образах базисных векторов.
A= 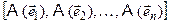
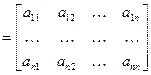 .
.
Для достижения поставленной цели необходимо ввести понятие расстояния от вектора до подпространства.
Дата добавления: 2020-07-18; просмотров: 556;











