Матричная форма замены базиса
Нетрудно видеть, что формулы (8.14), (8.15) являются отражением жорданова исключения переменной 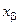 в системе линейных уравнений. Это позволяет формализовать процедуру замены базиса в матричной форме. Матричное решение может быть представлено следующей структурой
в системе линейных уравнений. Это позволяет формализовать процедуру замены базиса в матричной форме. Матричное решение может быть представлено следующей структурой
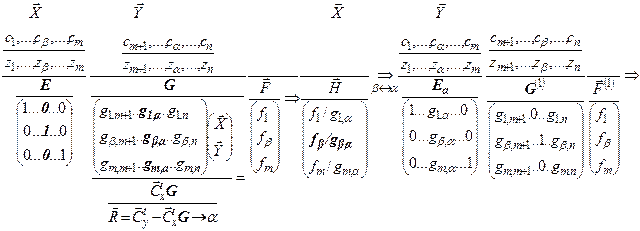
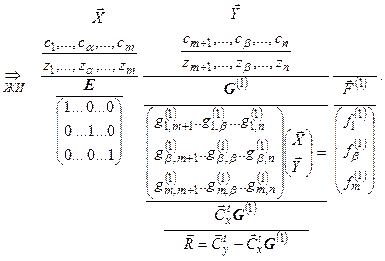
Первоначальная система представлена левой частью структуры: Целевая функция: 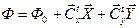 . Система линейных ограничений имеет вид:
. Система линейных ограничений имеет вид: 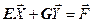 . Отсюда вектор зависимых переменных
. Отсюда вектор зависимых переменных 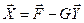 , а целевая функция
, а целевая функция 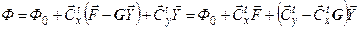
представляется только через независимые переменные 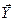 .
.
После определения варьируемой независимой переменной 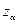 формируется столбец
формируется столбец 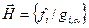 , анализ которого позволяет выделить выводимую из базиса переменную
, анализ которого позволяет выделить выводимую из базиса переменную 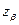 . Производится замена столбцов β матрицы Е и α матрицы
. Производится замена столбцов β матрицы Е и α матрицы 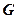 , а также обмен переменных в строках
, а также обмен переменных в строках 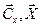 и
и 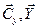 (правая часть первой структуры). Далее выполняется одновременное преобразование (жорданово исключение) объединенной матрицы
(правая часть первой структуры). Далее выполняется одновременное преобразование (жорданово исключение) объединенной матрицы 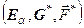 так, чтобы в левой части образовалась единичная матрица (вторая часть структуры). Промежуточная строка
так, чтобы в левой части образовалась единичная матрица (вторая часть структуры). Промежуточная строка 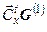 и результирующая
и результирующая 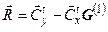 получаются матричными умножением и вычитанием указанных компонент.
получаются матричными умножением и вычитанием указанных компонент.
 Очередная варьируемая независимая переменная, как и на первом шаге, определяется по знаку и величине компонент вектора
Очередная варьируемая независимая переменная, как и на первом шаге, определяется по знаку и величине компонент вектора 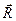 ,.Если всекомпонентыположительны, то решение найдено. При этом
,.Если всекомпонентыположительны, то решение найдено. При этом 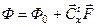 . Если имеется отрицательная компонента, - производится новый шаг расчетного процесса.
. Если имеется отрицательная компонента, - производится новый шаг расчетного процесса.
Дата добавления: 2020-07-18; просмотров: 611;











