Первый подход к поиску базиса.
В случае если в ограничениях задачи левая часть < либо 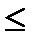 правой, используется первый подход к поиску базиса. Исходная система ограничений- неравенств преобразуется в систему равенств путём добавления свободных переменных, коэффициенты при которых равны единице.
правой, используется первый подход к поиску базиса. Исходная система ограничений- неравенств преобразуется в систему равенств путём добавления свободных переменных, коэффициенты при которых равны единице.
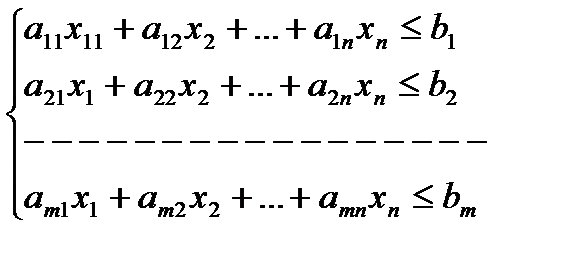
В каждое из ограничений системы добавляют свою свободную переменную. Для наглядности расположим их по диагонали.
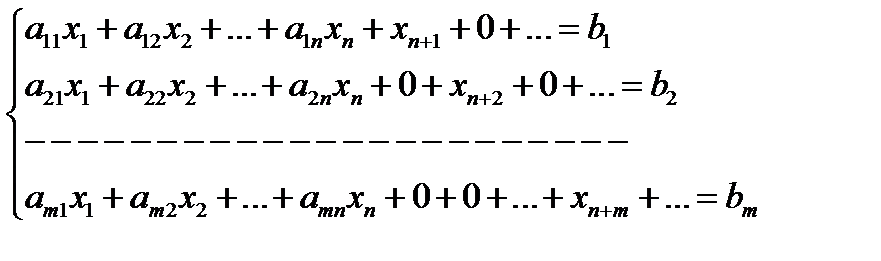
С экономической точки зрения свободные переменные представляют собой неиспользованные ресурсы, следовательно, их «цена» в целевой функции = 0, т. е. они не учитываются в целевой функции.
Коэффициенты при свободных переменных образуют единичную матрицу, определитель которой = 1. Это означает, что система не вырожденная и векторы-столбцы, компонентами которых являются коэффициенты соответствующих свободных переменных, линейно не зависимы и образуют базис.
Симплекс-метод основан на разложении векторов по базису. Условия задачи можно записать в виде векторов.
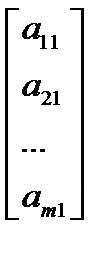 = P1
= P1 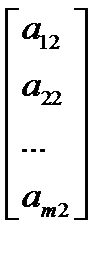 =P2……
=P2…… 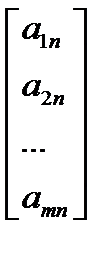 = Pn
= Pn
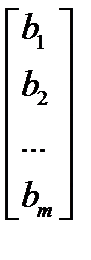 = P0 -вектор решений.
= P0 -вектор решений.
Дата добавления: 2019-12-09; просмотров: 756;











