Определение нового базисного решения (замена базиса)

Метод подстановки

Переменная 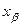выходит из базиса и становится независимой, в то время как 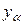входит в базис и становится зависимой. В силу изменения состава множества независимых переменных меняется и система (8.10). Новую систему можно получить подставляя 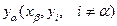из уравнения b системы (8.10)

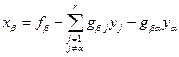
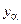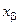во все остальные уравнения этой системы: Для этого выразим через и .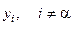

.

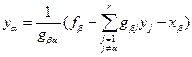Подставим полученное выражение в остальные уравнения:

.

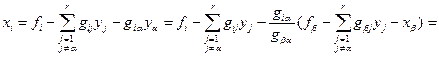
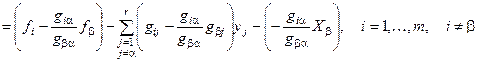В результате подстановки изменяются:

столбец свободных членов:

;

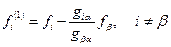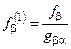
(8.14)

и элементы всех столбцов матрицы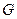

; .

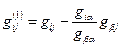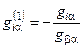(8.15)

Необходимо сделать пояснение относительно столбца a. Поскольку переменные 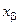и 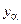поменялись местами, то на месте столбца a в новой матрице 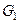будут стоять коэффициенты, связанные с 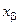, что и отражено в формуле (8.15).

После выполнения подстановки вновь образуется система из m уравнений, разрешенная относительно r = n – m независимых переменных. В новой системе независимых переменных 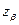заменяет 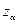. Новый базис является допустимым, поскольку, по условиям построения нового базиса ни одна из переменных не перешла через ноль. Последующая работа симплекс–метода аналогична описанной, но выполняется уже для другого базисного решения.