Метод искусственного базиса

Суть метода: в каждое уравнение, дающее отрицательную компоненту в базисном решении, вводим свою новую неотрицательную искусственную переменную у₁,у₂,…, у_k, которая имеет тот же знак, что и свободный член в правой части уравнения. В первой таблице включаем в число основных все искусственные переменные и те обычные добавочные переменные, которые определяют неотрицательные компоненты базисного решения. Составляем новую линейную функцию 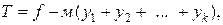где м - произвольно большое число, и ищем ее максимум (т-задача). Назовём м-функцией выражение 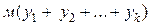. Справедлива теорема:

1. Если в оптимальном решении т-задачи все искусственные переменные равны 0, то соответствующие значения остальных переменных дают оптимальное решение исходной задачи (т.е. 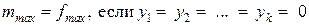т.е. минимум м-функции равен 0).

2. Если имеется оптимальное решение т-задачи, в котором хотя бы одна из искусственных переменных отлична от 0, то система ограничений исходной задачи несовместна.

3. Если Т_max= ∞, то исходная задача также неразрешима, причем либо f_max=∞, либо условия задачи противоречивы.

Из теоремы следует, что вначале следует найти минимум м- функции. если он равен 0 и все искусственные переменные обращаются в 0, то далее можно отбросить эти переменные и решать исходную задачу, исходя из полученного допустимого базисного решения. на практике находят не минимум м-функции, а максимум (-м)-функции.