Расстояние от вектора до подпространства.
 Из множества векторов, образующих Rn, можно выделить некоторое подмножество, обладающее свойствами линейного пространства, меньшей размерности
Из множества векторов, образующих Rn, можно выделить некоторое подмножество, обладающее свойствами линейного пространства, меньшей размерности 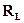 , L<n. В этом случае говорят, что
, L<n. В этом случае говорят, что 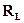 – подпространство пространстваRnи
– подпространство пространстваRnи 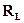 Ì Rn.
Ì Rn.
| Рис. 7.4. Расстояние от вектора до подпространства |
Для любого вектора 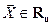 и не принадлежащего
и не принадлежащего 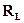 ,
, 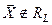 можно найти модуль разности векторов
можно найти модуль разности векторов 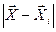 , где
, где 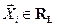 (рис. 7.4). Изменяя
(рис. 7.4). Изменяя 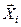 можно найти такой вектор
можно найти такой вектор 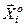 , который обеспечивает минимальную длину h разности
, который обеспечивает минимальную длину h разности 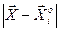 . Эта минимальная длина называется расстоянием от вектора
. Эта минимальная длина называется расстоянием от вектора 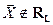 до подпространства
до подпространства 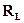 , т.е.
, т.е. 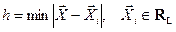 .
.
Объем “n” – мерного параллелепипеда, как обобщение понятий длины, площади, объема трехмерного параллелепипеда, определяется следующим образом.
1. Объем параллелепипеда, построенного на одном векторе 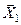 есть длина данного вектора:
есть длина данного вектора: 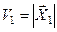 .
.
2. Если объем параллелепипеда 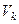 , образованного k векторами
, образованного k векторами 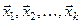 уже построен, то объем
уже построен, то объем 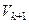 параллелепипеда, образованного векторами
параллелепипеда, образованного векторами 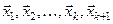 , выходящих из одной точки, равен
, выходящих из одной точки, равен 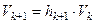 , где
, где 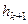 есть расстояние от конца вектора
есть расстояние от конца вектора 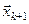 до подпространства
до подпространства 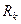 , образованного
, образованного 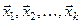 .
.
| Рис. 7.5. Объем параллелограмма |
3.  Параллелепипед, построенный на двух векторах
Параллелепипед, построенный на двух векторах 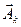 =(а11, а21)t,
=(а11, а21)t, 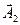 =(а12, а22)t является параллелограммом и объем (площадь) такого параллелепипеда равна произведению длины одного вектора на длину перпендикуляра проведенного из конца второго вектора на первый (на расстояние от второго вектора до первого),
=(а12, а22)t является параллелограммом и объем (площадь) такого параллелепипеда равна произведению длины одного вектора на длину перпендикуляра проведенного из конца второго вектора на первый (на расстояние от второго вектора до первого), 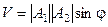 , где j -угол между векторами
, где j -угол между векторами 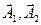 (рис. 7.5 ).
(рис. 7.5 ).
Перейдем к доказательству исходного тезиса относительно определителя матрицы.
Дата добавления: 2020-07-18; просмотров: 1092;











