Матрица перехода от базиса к базису
Пусть b = {b1, … , bn}– базис n-мерного векторного пространства V над полем F. Тогда L(b) = V, так что любой вектор v Î V является линейной комбинацией базисных векторов: v = a1×b1+…+an×bn. Напомним, что скаляры a1 , … , an Î F называются координатами вектора v в базисе b , а вектор-столбец 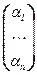 Î nF – координатным столбцом вектора v в базисе b и обозначается через [v]b . Было доказано, что координатные столбцы удовлетворяют следующим очевидным свойствам:
Î nF – координатным столбцом вектора v в базисе b и обозначается через [v]b . Было доказано, что координатные столбцы удовлетворяют следующим очевидным свойствам:
10. [0]b = 0 Î nF.
20. " u, v Î V [u+v]b= [u]b + [v]b .
30. " a Î F " v Î V [a×v]b = a×[v]b .
Пусть теперь e = {e1 , … , en} и f = {f1 , … , fn} – два базиса векторного пространства V. Тогда каждый вектор fiоднозначно разлагается по базису e : fi = e1×t1i + … + en×tni (1 £ i £ n). Таким образом, существует однозначно определённая матрица Te,f = (tij) Î M(n, F) со свойством f = e×Te,f. При этом по свойству 150 матричного символизма Te,f Î GL(n, F). Матрица Te,f называется матрицей перехода от базиса e к базису f.
Из определения немедленно следует, что fi = e1×t1i + … + en×tni = e×t(i). Таким образом, t(i) = [fi]eи Te,f = ([f1]e , … , [fn]e).
Примеры: 1. Пусть e =(e1 , e2, e3) – произвольный базис векторного пространства V , f = (e1 – e3 , e1 + e2 , 2×e2 + e3).
Тогда f = (e1 , e2 , e3)× 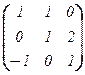 . При этом матрица Te, f =
. При этом матрица Te, f = 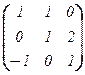 невырождена, т.е. f – базис V, а Te, f – матрица перехода от e к f.
невырождена, т.е. f – базис V, а Te, f – матрица перехода от e к f.
2. Пусть V = R n, e = (e1 , … , en) и f = (f1, … , fn) – два базиса. Известно, столбец [fj] находится из системы уравнений (e1t , … , ent)×[fi]e = fit. Поэтому матрица перехода Te,f = ([f1]e , … , [fn]e) удовлетворяет матричному уравнению (e1t , … , ent)×Te,f = (f1t , … ,f1t).
3.Если же V =nR , e = (e1 , … , en) и f = (f1, … , fn) – два базиса V, то аналогично предыдущему можно получить, что матрица Te,fоднозначно определяется системой линейных уравнений (e1 , … , en)×Te,f = (f1, … , fn).
4. Пусть V = R3, e = ((1; 0; 1), (–1; 1; 0), (0; 0; 1)), f = ((0; 0; –1), (0; 1; 1), (2; 0; 0)). Для нахождения матрицы перехода Te,f записываем систему 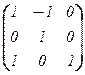 ×Te,f =
×Te,f = 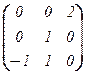 , решая которую, получаем
, решая которую, получаем
Te,f = 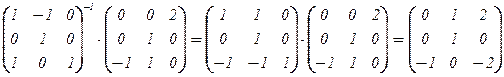 ×.
×.
Дата добавления: 2021-12-14; просмотров: 442;











