а) система Y-коэффициентов
Пусть воздействиями являются напряжения, а искомыми (откликами) будут токи. При такой постановке задачи токи 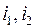 представляют собой некоторые функции напряжений
представляют собой некоторые функции напряжений 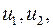 т.е.
т.е.
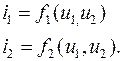 (5.1)
(5.1)
Соответствующие изменения токов определяются полными дифференциалами:
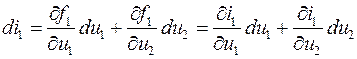 (5.2)
(5.2)

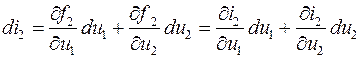 (5.2а)
(5.2а)
Входящие в эти уравнения в качестве коэффициентов частные производные имеют размерность проводимости и называются Y-коэффициентами четырехполюсника.
Введем обозначения:
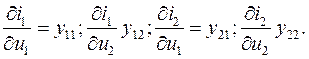
Тогда уравнения (5.2) и (5.2а) можно переписать так
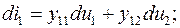 (5.3)
(5.3)
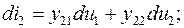 (5.3а)
(5.3а)
Полученные дифференциальные соотношения справедливы при любой форме колебаний и любом виде цепи. Особый интерес представляет рассмотрение случая линейной цепи в режиме гармонических колебаний. В этом случае соотношения (5.3) и (5.3а) записываются для комплексных амплитуд напряжений и токов, т.е.
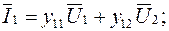 (5.4)
(5.4)
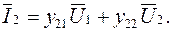 (5.4а)
(5.4а)
Комплексные Y-коэффициенты могут быть определены по результатам двух опытов: 1)при коротком замыкании выхода и при питании четырехполюсника слева (рис.5.2а); 2) при короткозамкнутом входе и при питании четырехполюсника справа (рис.5.2б). Они могут быть определены экспериментально или теоретически рассчитаны по следующим формулам:
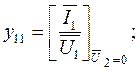
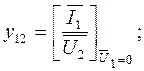
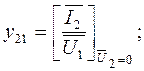
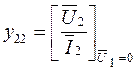 .
.
Систему уравнений (5.4), (5.4а) можно записать в более компактной (матричной) форме:
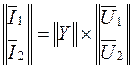 , (5.5)
, (5.5)
где 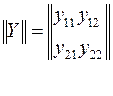 - матрица проводимостей, или Y-матрица.
- матрица проводимостей, или Y-матрица.
Для пассивного четырехполюсника, т.е. четырехполюсника, внутри которого нет источников энергии, выполняется соотношение
y12=y21 (5.6)
В симметричном четырехполюснике
y11=y22, (5.7)
т.е. в симметричном пассивном четырехполюснике входная и выходная проводимости равны между собой.
Уравнения, связывающие токи входа и выхода с напряжениями входа и выхода записываются в виде
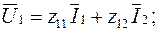 (5.8)
(5.8)
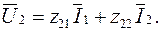 (5.8а)
(5.8а)
Z-коэффициенты определяются из опытов холостого хода на входе и выходе.
Когда четырехполюсник выполняет роль промежуточного звена между источником и сопротивлением нагрузки, заданными величинами часто являются параметры нагрузки 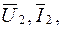 а искомыми величины, характеризующие режим на входе четырехполюсника (
а искомыми величины, характеризующие режим на входе четырехполюсника ( 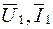 ), что соответствует системе уравнений типа А:
), что соответствует системе уравнений типа А:
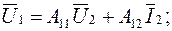 (5.9)
(5.9)
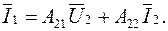 (5.9а)
(5.9а)
Для рассматриваемой задачи, когда выход четырехполюсника подключен к нагрузке, целесообразно положительные направления напряжений и токов выбрать такими, какие приняты в схеме на рис. 5.2.
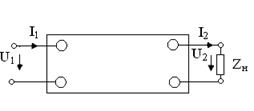
Рис. 5.2
Значения каждого из A-коэффициентов определяются из двух опытов: опыта холостого хода выхода (I2 =0) и опыта короткого замыкания выхода (U2=0).
Основные уравнения четырехполюсника в А-коэффициентах можно записать в матричной форме
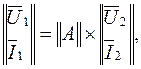 где
где 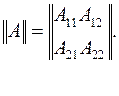 (5.10)
(5.10)
Когда заданными являются комплексные амплитуды тока на входе 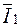 и напряжения
и напряжения 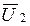 (вариант 4, табл 5.1), , искомые величины
(вариант 4, табл 5.1), , искомые величины 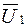 , и
, и 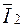 могут быть найдены, если выразить основные уравнения четырехполюсника в так называемых h-коэффициентах:
могут быть найдены, если выразить основные уравнения четырехполюсника в так называемых h-коэффициентах:
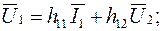 (5.11)
(5.11)
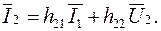 (5.11а)
(5.11а)
Значения каждого из h-коэффициентов определяются из двух опытов: короткого замыкания выхода (U2=0) и холостого хода первичной цепи (I1=0).
В том случае, когда задаются величины 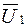 и
и 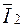 (вариант 5, табл 5.1), остальные две величины из уравнений
(вариант 5, табл 5.1), остальные две величины из уравнений
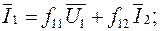 (5.12)
(5.12)
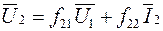 . (5.12а)
. (5.12а)
Входящие так называемые f-коэффициенты могу быть найдены из двух опытов: холостого хода вторичного тока (I2=0) и короткого замыкания на входе (U1=0).
Последний возможный вариант записи основных уравнений четырехполюсника (вариант 6, табл 5.1):
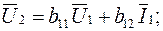 (5.13)
(5.13)
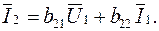 (5.13а)
(5.13а)
Значения b-коэффициентов определяются опытами холостого хода входной цепи (I1=0) и короткого замыкания входа (U1=0).
Последние три системы уравнений могут быть записаны в матричной форме подобно (5.10).
Выбор того или иного типа уравнений четырехполюсника зависит исключительно от той или иной задачи, которая в данном случае решается. Уравнения типа h, например, часто применяется при рассмотрении схем с транзисторами, так как режим транзистора определяется входным током I1 и выходным напряжением U2.
Соотношения между элементами различных матриц даны в таблице5.2. Таблица 5.2.
| Из системы→ В систему↓ | Z | A | h | f | b |
| Z | 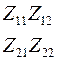
| 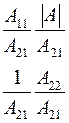
| 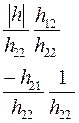
| 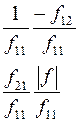
| 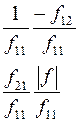
|
| Y | 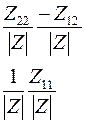
| 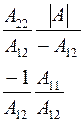
| 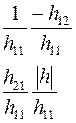
| 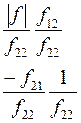
| 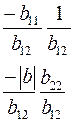
|
| A | 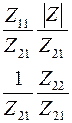
| 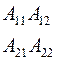
| 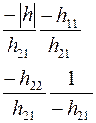
| 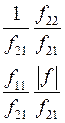
| 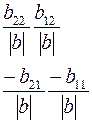
|
| h | 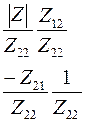
| 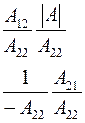
| 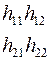
| 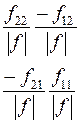
| 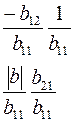
|
| f | 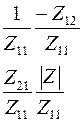
| 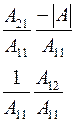
| 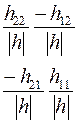
| 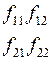
| 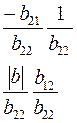
|
| b | 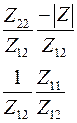
| 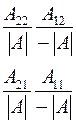
| 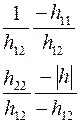
| 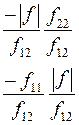
| 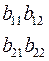
|
Примечание. 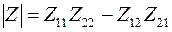
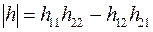
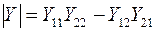
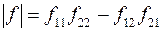
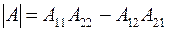
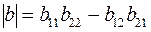 .
.
5. 3 Матрицы сложных четырехполюсников.
Сложный четырехполюсник может быть образован в результате соединения между собой нескольких, в частности, двух четырехполюсников. Если известны коэффициенты каждого из составляющих четырехполюсников, могут быть рассчитаны коэффициенты результирующего (эквивалентного) четырехполюсника. Этот расчет проще всего производить, оперируя с уравнениями в матричной форме.
Рассмотрим основные соединения четырехполюсников.
а). Наиболее важным соединением четырехполюсников является каскадное соединение, когда выходные зажимы первого четырехполюсника соединяются с входными зажимами второго (рис. 5.3).
При каскадном соединении выходное соединение первого четырехполюсника равно входному соединению второго, а выходной ток первого четырехполюсника равен входному току второго четырехполюсника, т. е.
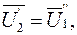
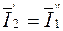 (5.14)
(5.14)
 а) б)
а) б)
Рис.5.3
Выразим уравнения исходных четырехполюсников через А-коэффициенты
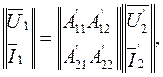
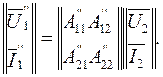
Используя свойства каскадного соединения (5.4), запишем
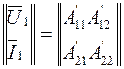
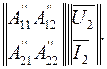
Таким образом, матрица сложного четырехполюсника (рис.5.3а) равна произведению матриц соединенных четырехполюсников:
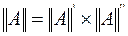 (5.15)
(5.15)
б) Последовательное соединение.
Под последовательным соединением понимается такое включение, при котором как входные, так и выходные их зажимы включены последовательно (рис.5.4а).
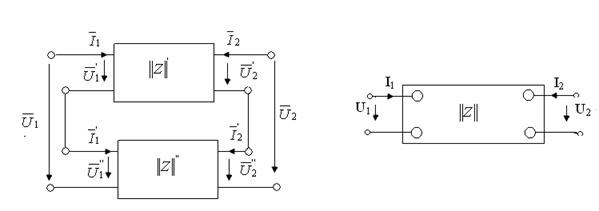
а) б)
Рис.5.4
Выразим уравнения исходных четырехполюсников через Z-коэффициенты. Тогда получим
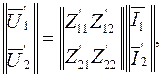 (5.16)
(5.16)
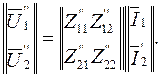 (5.17)
(5.17)
Результирующие напряжения и токи на входе и выходе при последовательном соединении будут:
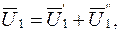
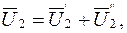
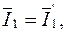
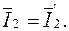
Поэтому, складывая (5.16) и (5.17), получим
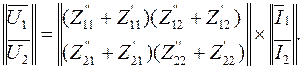 (5.18)
(5.18)
Таким образом, при последовательном соединении, 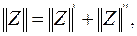 т.е. Z-матрица результирующего четырехполюсника (5.4б) равна сумме Z-матриц исходных четырехполюсников. Отсюда следует, что при расчете цепи последовательно соединенных четырехполюсников удобно пользоваться системой Z-коэффициентов.
т.е. Z-матрица результирующего четырехполюсника (5.4б) равна сумме Z-матриц исходных четырехполюсников. Отсюда следует, что при расчете цепи последовательно соединенных четырехполюсников удобно пользоваться системой Z-коэффициентов.
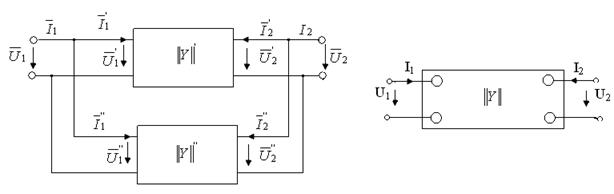
в) Параллельное соединение.
При последовательном соединении как входные, так и выходные зажимы четырехполюсников соединяются параллельно (рис.5.5а)
а) б)
Рис. 5.5
Используя систему Y=коэффициентов, запишем уравнения исходных четырехполюсников:
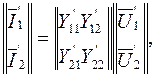 (5.19)
(5.19)
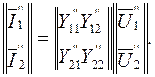 (5.20)
(5.20)
Так как в рассматриваемой схеме 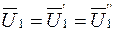 ,
, 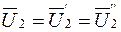 ,
, 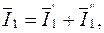
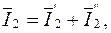 то, складывая (5.19) и (5.20), получим уравнение сложного четырехполюсника (рис. 5.5б):
то, складывая (5.19) и (5.20), получим уравнение сложного четырехполюсника (рис. 5.5б):
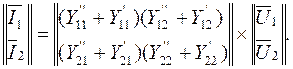 (5.21)
(5.21)
Отсюда следует, что 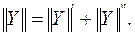
При параллельном соединении Y-матрица сложного четырехполюсника равна сумме Y-матриц исходных четырехполюсников.
г) Последовательно-параллельное соединение.
В этом случае входные зажимы исходных четырехполюсников соединяются последовательно, а выходные – параллельно (рис.5.6а)
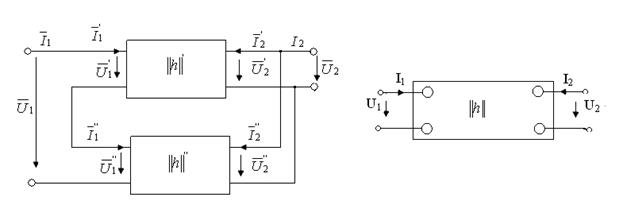
а) б)
Рис.5.6
Теперь воспользуемся системой h-коэффициентов и запишем уравнения четырехполюсников в виде:
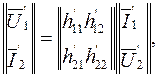 (5.22)
(5.22)
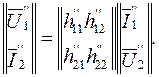 (5.23)
(5.23)
В схеме последовательно-параллельного соединения
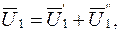
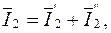
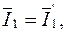
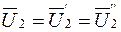 .
.
Поэтому для результирующего четырехполюсника (рис.5.6б) получим
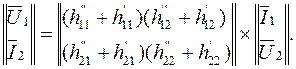
Таким образом 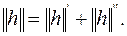
д) Параллельно последовательное соединение.
В рассматриваемой схеме (5.7а) входные зажимы исходных четырехполюсников соединены параллельно, а выходные – последовательно (рис.5.7а).
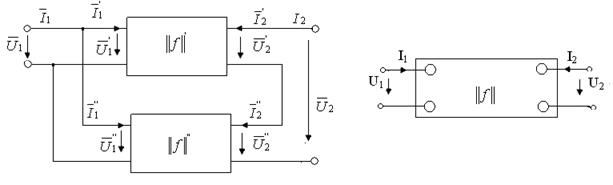 б)
б)
а)
Рис.5.7
Если в этом случае воспользоваться системой f-коэффициентов, уравнения примут вид
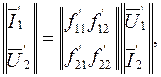 (5.24)
(5.24)
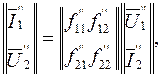 (5.25)
(5.25)
Из схемы на рис.5.6 следует 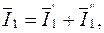
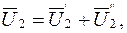
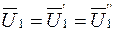 ,
, 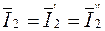 .
.
Поэтому, суммируя (5.24) и (5.25), для результирующего четырехполюсника (рис.5.7б) найдем
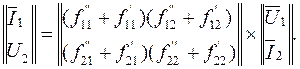 (5.26)
(5.26)
Таким образом 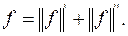
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Теоретические основы построения и функционирования специальных систем защиты от ОМП и пожаротушения. |
Дата добавления: 2020-10-25; просмотров: 928;











