В) Модель коэффициента трения
Погрешности расчета контактных напряжений, силы и мощности холодной прокатки существенно зависят от достоверности принятых значений коэффициентов трения в очаге деформации.
Методы определения напряжений трения и коэффициентов трения в процессах прокатки рассмотрены в разделе 5 этого учебника.
Для определения величины коэффициентов трения при расчете контактных напряжений, сил и мощности в процессах холодной прокатки используют справочные данные и эмпирические зависимости, подчас противоречащие друг другу. Эти противоречия вызваны тем, что коэффициент трения при холодной прокатке зависит от значительного количества факторов технологии и свойств прокатываемой полосы, которые в полном объеме воспроизвести во время лабораторных экспериментов невозможно. А в промышленных экспериментах, чтобы выявить влияние каждого параметра, его необходимо варьировать в широком диапазоне, что в большинстве случаев также невозможно из-за ограничений, установленных технологическим регламентом.
Широкое применение в энергосиловых расчетах процессов холодной прокатки получила формула А.П. Грудева [7], модифицированная применительно к изменениям сортамента и технологии, происшедшим в последние десятилетия 20 века [25]:
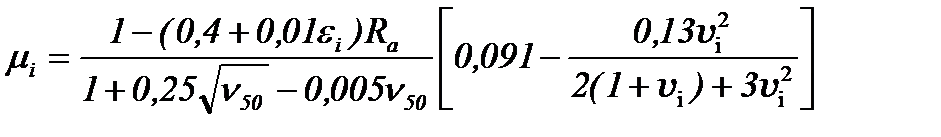 ,
,
где μi – коэффициент трения в очаге деформации i-ой клети многоклетьевого стана;
εi – частное относительное обжатие в i-ой клети, %;
Ra – среднеарифметическая высота микронеровностей поверхности бочки рабочих валков, мкм;
ν50 – кинематическая вязкость смазки (или эмульсола, из которого приготовлена смазочно-охлаждающая жидкость (СОЖ)) при 500С, сСт (мм2/с);
vi – скорость прокатки в i-ой клети, м/с.
Достоинство формулы А.П. Грудева состоит в том, что она физически обоснованно учитывает влияние на коэффициент трения ряда существенных факторов технологии холодной прокатки: шероховатости поверхности бочки, характеризуемой величиной Ra, смазывающих свойств СОЖ, характеризуемых величиной ν50, скорости прокатки vi. Однако она имеет существенный недостаток, снижающий достоверность найденных с ее помощью значений коэффициента трения и увеличивающих погрешности энергосилового расчета.
Он состоит в том, что она не учитывает фактор, оказывающий большое влияние на величину коэффициента трения – предел текучести прокатываемой полосы σт, σ0,2, возрастающий в процессе холодной прокатки в 2-3 раза из-за наклепа.
Поэтому для расчетов контактных напряжений в очагах деформации рабочих клетей станов холодной прокатки предпочтительнее использовать следующую регрессионную зависимость коэффициента трения от значимых факторов технологического процесса, предложенную в работе [28]:
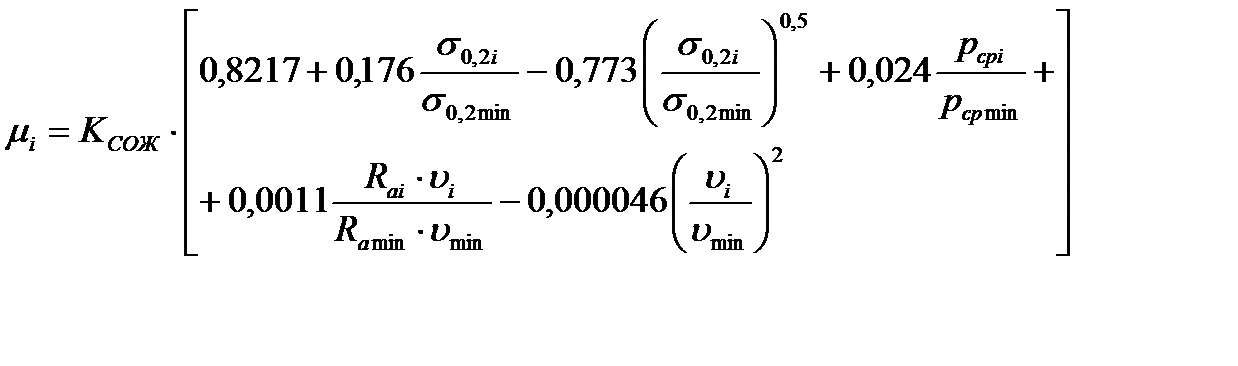 6.20)
6.20)
где σ0,2i, pсрi средние значения условного предела текучести полосы и нормального контактного напряжения в очаге деформации i-ой рабочей клети, МПа;
Rai – среднеарифметическая величина микронеровностей на поверхности бочки рабочих валков i-ой клети, мкм;
vi – скорость полосы на выходе из валков i-ой рабочей клети, м/с.
В уравнении (6.20) переменные параметры, влияющие на коэффициент трения, представлены в безразмерной форме, для чего в знаменатели всех членов введены их минимальные значения: σ0,2min = 200МПа, pср min = 400 МПа, Ra min = 0,6мкм, vmin = 1 м/с.
Кинематическая вязкость СОЖ при выводе формулы (6.20) была постоянной: ν50 = 30 сСт, что соответствует применяемым на многих станах эмульсиям, изготавливаемым из эмульсолов новых поколений (КВЭКЕРОЛ, ГЕРОЛЮБ и др.) При указанном значении ν5, входящий в формулу (6.20) коэффициент Kсож=1. При использовании СОЖ с другой вязкостью величину Kсож следует уточнять на стане путем адаптации формулы (6.20).
Расчет коэффициентов трения по уравнению (6.20) позволяет снизить погрешности расчетов усилия прокатки в среднем в 2 раза, до диапазона 5,4-8,5%, что для инженерных расчетов подобного класса считается весьма приемлемым результатом.
Достоверность формулы (6.20) повышается, если подставлять в нее значения шероховатости Ra с учетом износа поверхности бочки за время, прошедшее от момента установки в клеть отшлифованных или текстурированных валков до момента, для которого рассчитываются энергосиловые параметры. Изменение шероховатости вследствие износа предложено определять с помощью следующих регрессионных зависимостей:
- для шлифованных валков
Ra = Ra исх – 0,1141τ + 0,0064 τ2;
- для текстурированных валков:
Ra = Ra исх – 0,32τ + 0,18 τ2,
где Ra исх – исходное значение шероховатости,
τ – время, прошедшее с момента перевалки рабочих валков, час.
Эти выражения могут быть уточнены на каждом стане в процессе подготовки и эксплуатации валков, с учетом их материала, термообработки и износостойкости поверхностного слоя бочки, причем желательно, вместо времени работы валков, использовать длину (километраж) полос, прокатанных после перевалки.
Исходную величину Ra обеспечивают при подготовке поверхности бочки валков к установке в стан путем шлифовки или текстурирования, при этом необходимые значения Ra указывают в технологических нормативных документах стана, исходя из особенностей технологического процесса цеха и требований к качеству поверхности прокатываемых полос.
Если сведения о нормативных значениях шероховатости отсутствуют, можно задавать Ra, руководствуясь рекомендациями таблицы 6.1.
Таблица 6.1
Рекомендуемые значения шероховатости бочки рабочих валков Ra
по клетям непрерывного k-клетевого стана холодной прокатки
| Номер клети | 2,…,(k-1) | k | ||
| Вид обработки | шлифовка | текстурирование, насечка | шлифовка | |
| Значение Raисх, мкм | 1,8*) | 0,6 | 2,8 | 0,6 |
*) Примечание: при задании Ra для первой клети учитывается повышенная шероховатость горячекатаного подката.
В первой клети износ шероховатости валков можно не учитывать, т.к. коэффициент трения в ней зависит, главным образом, от шероховатости подката.
На рисунках 6.3, 6.4, 6.5, 6.6 показаны в графическом виде рассчитанные по уравнению (6.23) зависимости коэффициента трения от каждого фактора, влияющего на его величину. При построении этих графиков изменяли только один фактор, все остальные принимали неизменными.
Из графика рис. 6.3 видна существенная зависимость коэффициента трения от условного предела текучести прокатываемой полосы: при росте условного предела текучести от уровня 250-350 МПа, соответствующего его значениям в 1-й клети, до уровня 700-800 МПа, соответствующего упрочненному состоянию полосы в последней клети, коэффициент трения при шероховатости валков Ra = 0,6 мкм уменьшается в 4-6 раз: от 0,15-0,17 до 0,025-0,04. Очевидно, этот фактор является главной причиной высоких значений коэффициента трения в первых клетях непрерывных станов.
Увеличение шероховатости бочек рабочих валков вызывает рост коэффициента трения (рис. 6.4), однако градиент этого роста существенно зависит от
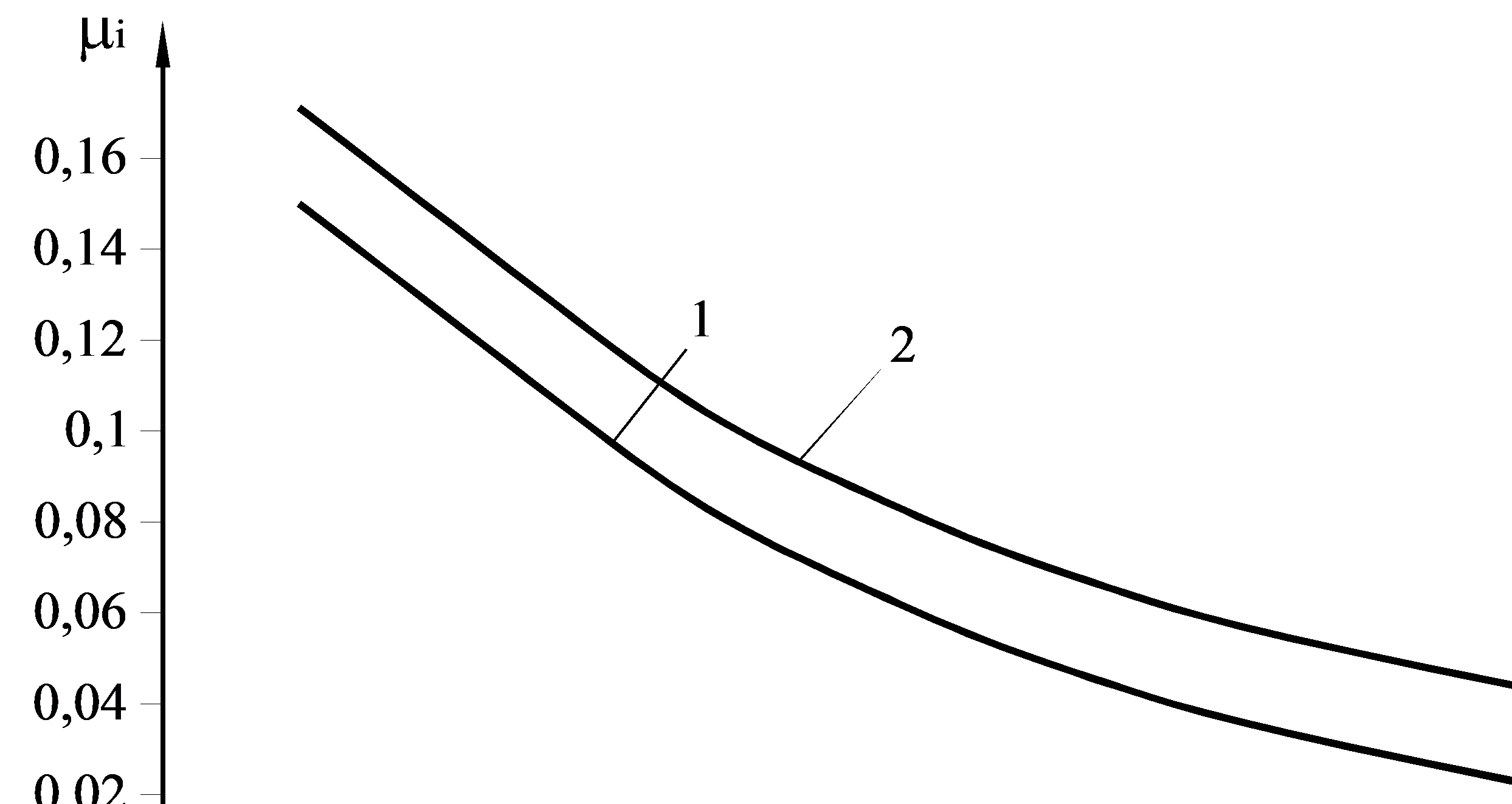
Рис.6.3. Зависимость коэффициента трения от условного предела текучести прокатываемой полосы (скорость прокатки vi = 10 м/с; шероховатость поверхности бочек валков Ra = 0,6 мкм) при средних значениях контактных напряжений pсрi:
1 – 450 МПа; 2 – 750 МПа.
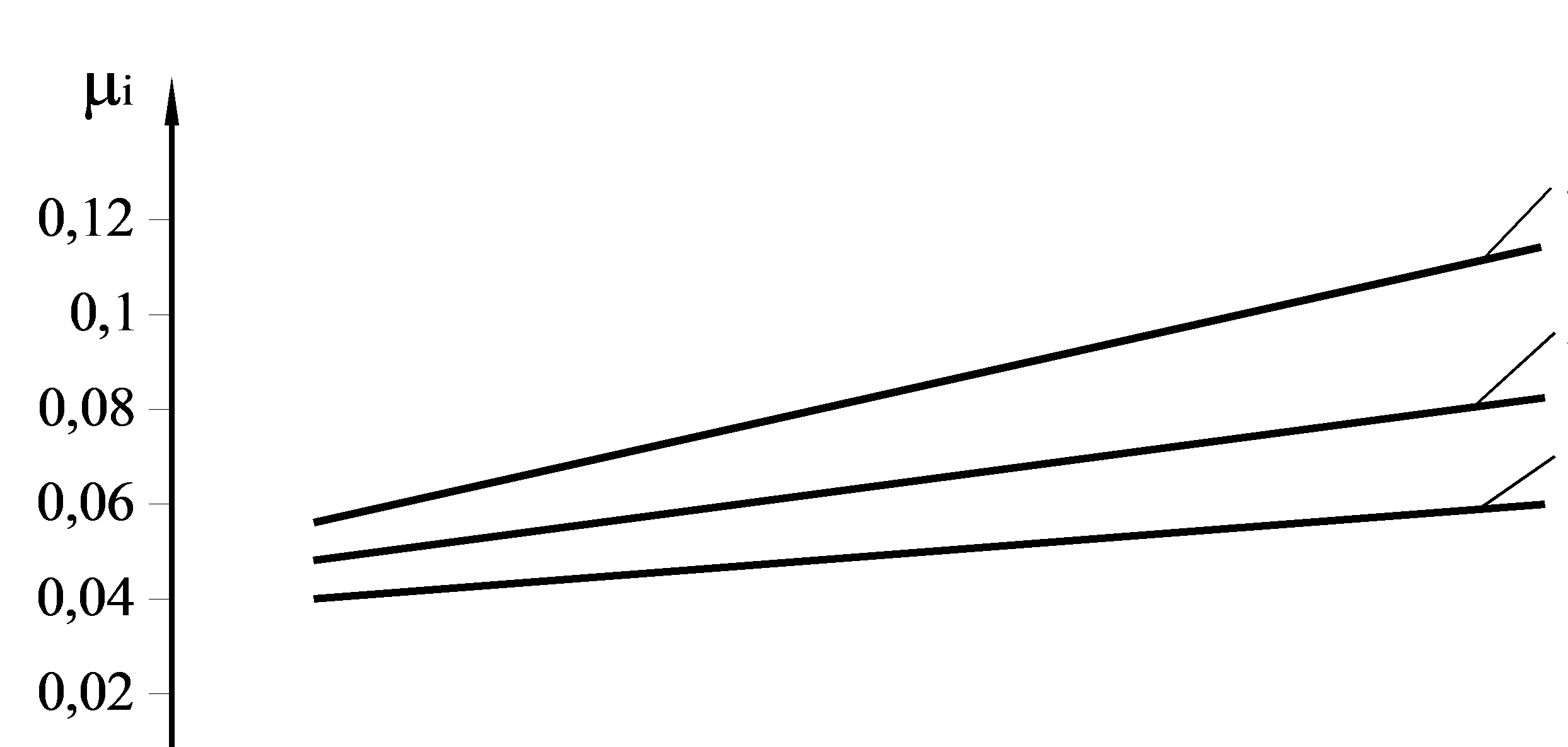
Рис. 6.4. Зависимость коэффициента трения от шероховатости поверхности валков (контактное напряжение pсрi = 750 МПа; предел текучести прокатываемой полосы σ0,2i = 700 МПа) при скоростях прокатки vi: 1 – 5 м/с; 2 – 10 м/с; 3 – 15 м/с.
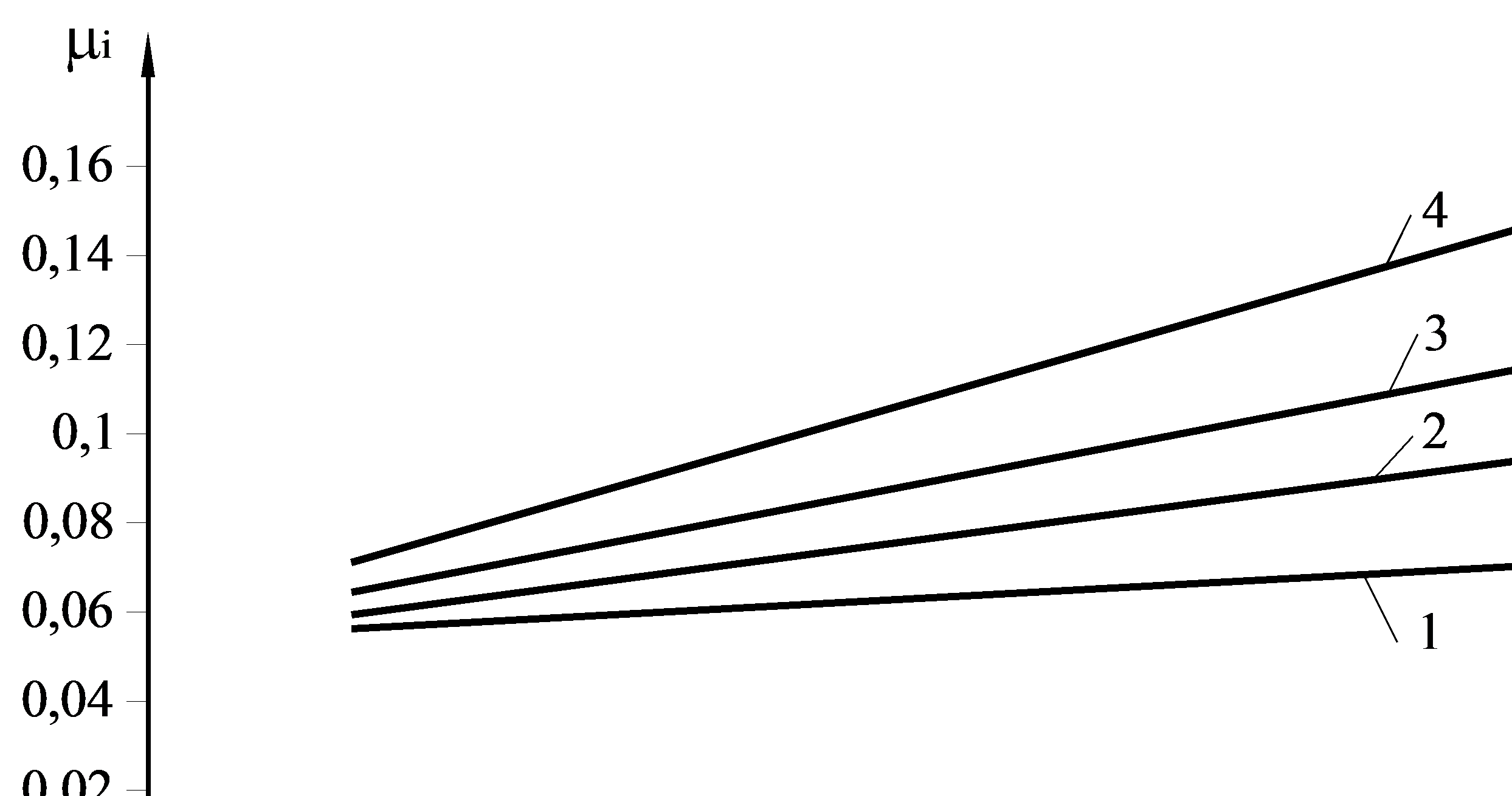
Рис. 6.5. Зависимость коэффициента трения от скорости прокатки (контактное напряжение pсрi = 750 МПа; предел текучести прокатываемой полосы σ0,2i = 600 МПа) при различной шероховатости поверхности валков Ra:
1 – 0,2 мкм; 2 – 1,0 мкм; 3 – 1,5 м/с; 4 – 2,5 м/с.
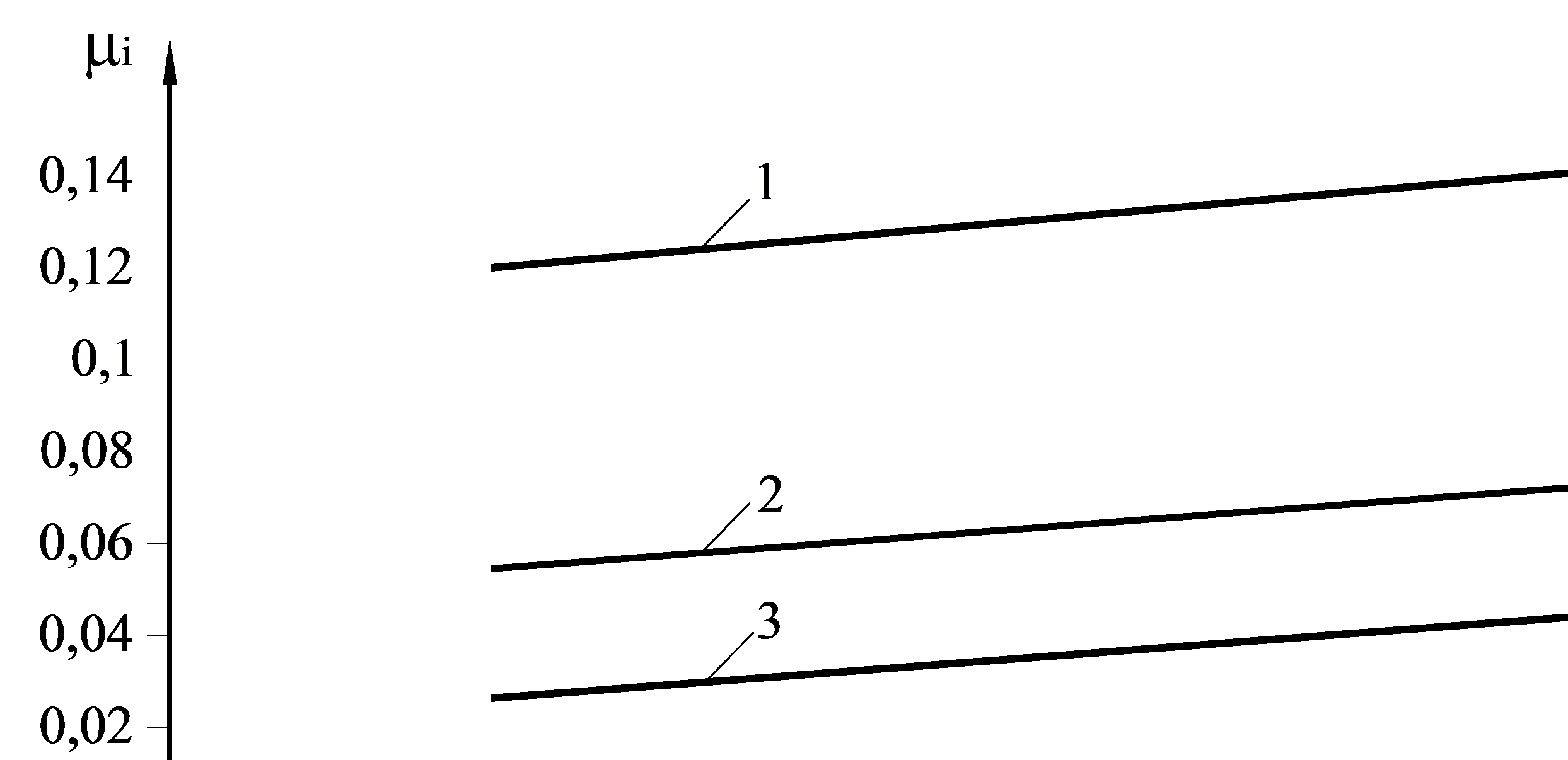
Рис. 6.6. Зависимость коэффициента трения от среднего удельного давления в очаге деформации (скорость прокатки vi = 10 м/с; шероховатость поверхности валков Ra=0,6 мкм) при значениях условного предела текучести полосы:
1 – 400 МПа; 2 – 600 МПа; 3 – 800 МПа.
скорости прокатки. При скорости vi=5 м/с, соответствующей скоростному режиму первых клетей, увеличение шероховатости в 5 раз (от Ra = 0,5 мкм до Ra = 2,5 мкм) приводит к росту коэффициента трения на 15-25%, а такое увеличение шероховатости при скорости vi=15 м/с (кривая 3 на рис. 8.4), соответствующей скоростному режиму последних клетей, вызывает рост коэффициента трения почти в 2 раза.
Графические зависимости коэффициента трения от скорости прокатки, рассчитанные по уравнению (6.20), показаны на рис. 6.5. Из графиков видно, что с ростом скорости прокатки коэффициент трения увеличивается, особенно это увеличение значительно при максимальной шероховатости валков. Следует отметить, что при изменении скорости прокатки на коэффициент трения влияют две противоположно действующие тенденции. С одной стороны, рост скорости прокатки способствует увеличению количества СОЖ, поступающей в очаг деформации, что уменьшает коэффициент трения. С другой стороны, повышение скорости прокатки разогревает СОЖ, снижая ее кинематическую вязкость, что увеличивает коэффициент трения. Графики рис. 6.5 свидетельствуют о преобладании последней тенденции.
Влияние среднего значения контактного напряжения на коэффициент трения показано на графиках рис. 6.6. Зависимости μi от pсрi при постоянных значениях остальных факторов являются линейными: увеличение pсрi на 100 МПа вызывает рост коэффициента трения примерно на 0,005.
Поскольку при вычислении значений μi величины pсрi заранее неизвестны, первоначальное значение pсрi задают приближенно, например 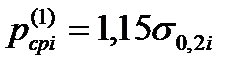 , а затем уточняют в цикле расчета усилия прокатки методом, изложенным в главе 8.
, а затем уточняют в цикле расчета усилия прокатки методом, изложенным в главе 8.
Дата добавления: 2019-02-08; просмотров: 1618;











