Образование сложных высказываний
В логике высказываний, этом простейшем разделе символической логики, абстрагируются не только от содержания, как это свойственно вообще всей логической науке, но и от составных частей и структуры суждений (хотя в логике предикатов их все же снова принимают во внимание). Суждение, как мы помним, обладает двумя важнейшими для логики свойствами: 1) быть либо истинным, либо ложным и 2) что-либо утверждать или отрицать. В структуру суждения входят субъект, предикат, связка и квантор, его поэтому можно охарактеризовать по количеству (как общее или частное) и качеству (как утвердительное и отрицательное). В наиболее простом разделе символической логики, который мы сейчас рассматриваем, в логике высказываний, характеристики мысли, обусловленные субъектно-пpедикатной структурой высказываний, выпадают, как отмечено, из рассмотрения, так что от всей мысли, когда она предстает как высказывание, в поле зрения, помимо чисто формальных связей с другими мыслями, остается одна лишь ее способность - быть либо истинной, либо ложной. Только в этом отношении высказывание сохраняет сходство с суждением. Правда, в учебниках иногда их все же именуют суждениями и даже раздел, где ведется речь об образовании сложных высказываний, чаще всего называется “Сложные суждения”. В этом нет большой ошибки, если не забывать сделанные оговорки. К такому названию мы тоже будем прибегать, дабы сохранить единство с общепринятым изложением этой темы. Но, тем не менее, нельзя забывать: каждое высказывание обладает только одним свойством суждения - быть либо истинным, либо ложным. Все остальные не рассматриваются, от них отвлекаются. Стало быть, упрощение предложений здесь простирается еще дальше.
Символический язык рассматриваемого раздела логики создается прежде всего путем введения переменных A, B, C, D,... р, q, r,... для высказываний, которые получили название пропозициональных переменных, и символических обозначений - для так называемых логических союзов или логических связок. Переменные ставятся вместо каких-нибудь повествовательных предложений, каковые, следовательно, выступают денотатами этих переменных, а их значения колеблются между двумя альтернативами: 1) быть истинными, 2) быть ложными.
Пропозициональными переменными пользуются так же, как в математике числовыми переменными. Там говорят, например, о натуральных, целых или рациональных числах a, b, c,... и их отношениях и составляют формулы с помощью этих символов. В логике высказываний говорят о высказываниях p, q, r,... и их отношениях и также с помощью этих символов составляют формулы. Если такая формула пригодна для выражения связей любого высказывания p, q, r, то, пока с ней производят операции по законам символической логики, она как бы сохраняет в себе в свернутом, сокращенном виде все то, что содержится в соответствующих предложениях, и после завершения преобразований новую формулу можно снова развернуть в высказывание.
Прежде всего символическая логика позволяет образовывать так называемые сложные суждения, которые составляются из простых, соединяясь с помощью различных логических союзов, называемых иногда также логическими операторами. Часть этих союзов имеет некоторое сходство с грамматическими союзами “и” и “или”, которые объединяют отдельные предложения, сводя их в сложные формулировки. Но полного сходства между ними нет, тем более что некоторые логические союзы вовсе не выглядят как грамматические союзы, а, например, отрицание вообще ничего не соединяет, потому что относится всегда к одному (хотя иногда и сложному) высказыванию; оно просто преобразует исходную мысль, дает ей иную форму, присоединяя к ней каждый раз одно и то же стандартное выражение. Hаиболее важными логическими союзами являются шесть: отрицание, конъюнкция, дизъюнкция (строгая и нестрогая), импликация, эквивалентность. В некоторых специальных случаях используются еще и другие, но мы о них говорить не будем. В нашу задачу входит рассмотрение лишь самых общих и самых употребительных логических операций логики высказываний.
Hам надо не только перебрать и уяснить способы создания сложных суждений, но и научиться определять их семантические значения в зависимости от значений истинности каждого из исходных высказываний, ибо они могут быть как истинными, так и ложными каждое. Возможные простейшие комбинации суждений с разными союзами сведены в одну таблицу (см. таблицу 1), называемую таблицей истинности сложных суждений. В символической логике принято обозначать истинное выражение единицей, а ложное - нулем. Стало быть, в приведенной дальше таблице 1 и 0 заменяют соответственно слова “истинно” и “ложно”.
Отрицание. Этот логический союз образуется за счет добавления к любому высказыванию слов: “Неверно, что...”. Существует много разных способов записывать отрицание в виде формулы (вообще символика в логике высказываний пока не является устоявшейся). Мы будем использовать для этих целей черту над переменными или формулами: 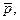
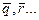 Читается: “Hевеpно, что p”, или просто: “Hе-p”. Аналогично обстоит дело с другими переменными. И если p означает, скажем, “Погода сегодня холодная”, то
Читается: “Hевеpно, что p”, или просто: “Hе-p”. Аналогично обстоит дело с другими переменными. И если p означает, скажем, “Погода сегодня холодная”, то 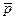 станет высказыванием: “Hевеpно, что погода сегодня холодная”. В результате приложения к исходной мысли этого логического союза образуется высказывание, истинность которого, как легко догадаться, меняется на противоположную. Так, если суждение “Погода сегодня холодная” истинно, то тогда высказывание “Неверно, что погода сегодня холодная”, очевидно, будет ложным. А если бы оно, наоборот, было ложным, то тогда после отрицания мы, естественно, получили бы истинное высказывание. Для любой пары взаимоотрицающих высказываний такое соотношение является непреложным: когда одно из них истинно, то другое обязательно ложно и наоборот.
станет высказыванием: “Hевеpно, что погода сегодня холодная”. В результате приложения к исходной мысли этого логического союза образуется высказывание, истинность которого, как легко догадаться, меняется на противоположную. Так, если суждение “Погода сегодня холодная” истинно, то тогда высказывание “Неверно, что погода сегодня холодная”, очевидно, будет ложным. А если бы оно, наоборот, было ложным, то тогда после отрицания мы, естественно, получили бы истинное высказывание. Для любой пары взаимоотрицающих высказываний такое соотношение является непреложным: когда одно из них истинно, то другое обязательно ложно и наоборот.
Это положение, несмотря на его кажущуюся самоочевидность и простоту, имеет важные следствия. Из-за него используемое в логике высказываний отрицание имеет существенные отличия от отрицания в обычном литературном языке. Допустим, кто-нибудь говорит: “X - студент третьего курса философского факультета МГУ”. И предположим, кто-то с ним не соглашается: “Неверно, что X - студент третьего курса...”. Под этим могут подразумеваться самые разные обстоятельства: X может в самом деле учиться на философском факультете, но не в МГУ, а в пединституте, он может быть студентом этого факультета МГУ, но не третьего курса, может быть и так, что отрицающий хочет сказать, что X - вообще не студент. Любое из соответствующих высказываний будет отрицанием исходного. Однако упомянутое положение об обязательной истинности одного из пары взаимоотрицающих утверждений может не выполняться. В самом деле. Возьмем два таких несовместимых высказывания: “X - студент третьего курса философского факультета МГУ” и “X - студент пятого курса философского факультета МГУ”. Хотя они не могут быть одновременно истинными, тем не менее сказать, что одно из них истинно, а другое ложно нельзя, потому что они оба могут быть ложными, если на самом деле X учится на философском факультете пединститута.
Поэтому такого рода внутренние, как их иногда называют, отрицания не принимаются во внимание в логике высказываний. Вернее говоря, они рассматриваются как конкретные разновидности внешнего отрицания “Неверно, что...” Так, если, например, перед нами утверждение: “Колхоз “Заря” убрал урожай зерновых за шесть дней”, а рядом стоит его отрицание, но в такой форме: “Колхоз “Заря” убрал урожай зерновых за три дня”, то прежде чем распространять на него правила логики высказываний, строго говоря, надо сначала переформулировать отрицающее утверждение в такое, которое в этом виде логического исчисления используется: “Неверно, что колхоз “Заря” убрал урожай зерновых за шесть дней”. Вот тогда к этой паре суждений можно применять без ограничений теорию, разработанную в рамках исчисления высказываний. Правда, в большинстве случаев такая переформулировка все-таки не требуется. Достаточно помнить о ней на тот случай, если возникнет недоразумение.
Еще одной особенностью отрицания в символической логике является то, что двойное отрицание само себя нейтрализует. Так что всегда справедливо выражение
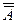 =А. (1)
=А. (1)
Знак равенства говорит только о том, что выражения взаимозаменимы. Переменная A означает любое простое или сложное высказывание, (любую формулу). Эта запись говорит о том, что высказывание с двумя отрицаниями равносильно тому же высказыванию без отрицания. Она представляет собой один из принципов символической логики, и мы поэтому будем отмечать такие, введя для них сплошную нумерацию. Данное положение можно обобщить для случая, когда отрицаний несколько. Что, например, подразумевается под выражением: “Неверно, что неверно, что неверно, что неверно, что книга интересная”? Это легко установить с помощью сделанных только что замечаний. Так как отрицание обязательно меняет истинность, то повторное отрицание ее снова восстанавливает. Пара отрицаний сводят друг друга на нет, поэтому любое четное число отрицаний можно убирать, если они возникли в процессе обработки или преобразования формулы. Стало быть, приведенное здесь длинное высказывание эквивалентно такому короткому: “Книга интересная”. Таким образом, мы получаем общее правило: высказывания, отрицающиеся несколько раз, равносильны одному отрицанию (когда их общее число нечетно) или отсутствию отрицания (когда их число четно и они попарно компенсируют друг друга).
В естественных языках повторные отрицания встречаются в виде стилистического приема и их число обычно не превышает двух. Можно, например, сказать: “Книга небезынтересная”, “Зима не бесснежная”. Как правило, этим хотят сказать, что признак в какой-то степени относим к обсуждаемому предмету: зиму нельзя считать полностью бесснежной - снег все-таки был, книга все же мало-мальски интересна. Эти оттенки смысла отрицания не учитываются в символической логике, потому что они сильно зависят от контекста, и подвести их под какое – то общее и в то же время простое правило вряд ли удастся.
Таблица 1
| p | q | 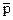
| (p 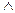 q) q)
| (p 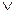 q) q)
| (p 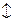 q) q)
| (p 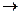 q) q)
| (p 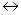 q) q)
|
| - - |
Конъюнкция. Следующее сложное высказывание, конъюнкция, представляет собой соединение двух и более высказываний с помощью союза “и”. Ее обозначение чаще всего такое: p 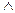 q; читается: p и q. Допустим, у нас имеется высказывание с союзом “и”: “Поезд следует до Москвы и отходит через пятнадцать минут”. Мы можем разбить его на две части, обозначив каждую часть соответственно буквами p и q: “Поезд следует до Москвы” (p) и “Поезд отходит через пятнадцать минут” (q). И тогда наше первоначальное высказывание может быть записано в виде приведенной формулы. Каждый из отдельных простых компонентов, стоящих по обе стороны от знака конъюнкции, мы будем называть конъюнктами. Сама по себе такая запись, конечно же, еще не продвигает вперед, еще никак не обновляет наши возможности в анализе подобных мыслей. Однако с ее помощью представляется возможным определить семантическое значение всего сложного утверждения, когда нам будет известно значение каждого компонента. В таблице истинности (табл. 1) приводятся все возможные комбинации для них.
q; читается: p и q. Допустим, у нас имеется высказывание с союзом “и”: “Поезд следует до Москвы и отходит через пятнадцать минут”. Мы можем разбить его на две части, обозначив каждую часть соответственно буквами p и q: “Поезд следует до Москвы” (p) и “Поезд отходит через пятнадцать минут” (q). И тогда наше первоначальное высказывание может быть записано в виде приведенной формулы. Каждый из отдельных простых компонентов, стоящих по обе стороны от знака конъюнкции, мы будем называть конъюнктами. Сама по себе такая запись, конечно же, еще не продвигает вперед, еще никак не обновляет наши возможности в анализе подобных мыслей. Однако с ее помощью представляется возможным определить семантическое значение всего сложного утверждения, когда нам будет известно значение каждого компонента. В таблице истинности (табл. 1) приводятся все возможные комбинации для них.
В первой строке берется случай, когда оба простых высказывания истинны. Как это понимать? Предположим, нам передали вот эту самую информацию о поезде на Москву и времени его отправления. И если мы затем выясним, что и первая и вторая части этого сообщения соответствуют действительности, то есть высказывания “Поезд следует до Москвы” и “Поезд отправляется через пятнадцать минут” оба истинны (p=1; q=1), то, очевидно, и всю информацию в целом мы тоже оценим как истинную. Это и отмечается в колонке для конъюнкции (первая строка) единицей. Теперь разберем другой вариант. Допустим, что истинным является только одно простое высказывание, скажем, второе, первое же ложно (p=0; q=1). То есть нам сказали, что поезд отходит на Москву через пятнадцать минут, но он отходит, хотя и в самом деле через пятнадцать минут, но не на Москву, как было сказано, а в каком-нибудь ином направлении. Как тогда будет оценено нами полученное сообщение в целом? Очевидно, оно вводит нас в заблуждение, и мы должны отнести его к разряду ложных. Этим объясняется цифра ноль во второй строке в колонке конъюнкции. Понятно, что при обратных значениях компонентов (p=1; q=0) будет то же самое - в целом информация по-прежнему ложна. Наконец, когда оба простых высказывания являются ложными суждениями, то тем более все суммарное высказывание представляет собой обман.
Таким образом, конъюнкция является истинной только тогда, когда оба составляющих ее простых высказывания истинны, при всех же остальных значениях входящих в нее переменных она ложна.
Не всегда конъюнктивные высказывания выражаются с помощью явно включенного в него союза “и”. Иногда вместо него может стоять только запятая или слова вроде: “также”, “наряду с...”, “ как то, так и другое”, “не только то, но и другое”, “но”, “зато” и пр.
Уже на этой стадии рассмотрения мы можем ввести пару простых положений:
(A 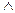 A)=A,
A)=A,
(A 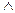 B)=(B
B)=(B 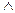 A).
A).
Первая из этих формул выражает так называемое правило идемпотентности. Его содержание самоочевидно: двух - (и многократное) повторение одного и того же высказывания через союз “и” равнозначно тому, если сказать один раз. Однако оно играет важную роль в преобразованиях, так как позволяет упрощать формулы, когда после ряда логических операций в них образовались выражения, содержащие повторение через конъюнкцию одной и той же переменной. Другая формула является выражением широко известного далеко за пределами символической логики правила коммутативности: последовательность написания конъюнктов не играет принципиальной роли - их можно переставлять местами.
Дизъюнкция (нестрогая). Этот логический оператор используется для отображения различного рода альтернатив. Дизъюнкция - соединение с помощью союза “или” (иногда пишется “или..., или”) двух и более высказываний, которые допускают их одновременную истинность (хотя бывает и так, что истинным является только одно из них). Ее символическая запись - pÚq; читается: p или q. Мы будем в дальнейшем называть дизъюнктами компоненты, из которых составляется дизъюнкция. Чтобы разобраться с ее значениями по истинности в таблице 1, приведем какой-нибудь конкретный пример. Возьмем высказывание “Этот вопрос решается или через управляющего, или через его заместителя”. В нем указывается на два возможных способа решить какой-то вопрос. Один из них задается высказыванием “Этот вопрос решается через управляющего” (обозначим его через p), другой - высказыванием “Этот вопрос решается через заместителя” (q). Попробуем перебрать все варианты, как это было с конъюнкцией.
Допустим, данную справку мы получили в каком-нибудь учреждении и после этого выяснили, что оба начальника в состоянии решить и решают такие вопросы. Стало быть, истинны как p, так и q (p=1; q=1). Как можно оценить истинность всего полученного указания? Вообще говоря, возможны случаи, когда такие высказывания вводят в заблуждение, если они означают, что только один из них компетентен заниматься данным делом, но не оба вместе. Но могут быть и такие обстоятельства, когда нам достаточно знать, где искать нужную инстанцию, остальное пока безразлично, и тогда то же самое указание при тех же значениях истинности простых суждений будет оценено как истинное. В символической логике предусмотрены оба варианта. Нестрогая дизъюнкция охватывает второй случай - при истинности обоих высказываний она является истинной. Поэтому в таблице истинности, в самой первой строке, где p=1; q=1, для нестрогой дизъюнкции указано значение 1. Когда же, далее, одно из простых суждений истинно (один из указанных руководителей занимается этим вопросом - причем все равно кто, - а другой не занимается) то, само собой понятно, у нас нет никаких оснований считать данную нам справку ложной: нам именно это и сказали, что обращаться надо к тому или другому. Стало быть, в колонке для нестрогой дизъюнкции и во второй, и в третьей строках (как и в первой) должна стоять 1. Ну а когда оба простых высказывания ложны, то, очевидно, у нас есть причины считать, что нас просто обманули - все дизъюнктивное высказывание надо считать в этом случае, конечно, ложным.
Последовательность написания дизъюнктов не влияет на истинность сложных высказываний, образованных с помощью союза “или”. Поэтому на нестрогую дизъюнкцию тоже распространяется правило коммутативности. Сохраняет свою силу и правило идемпотентности.
(A 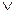 B)=(B
B)=(B 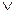 A),
A),
(A 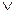 A)=A.
A)=A.
Дизъюнкция (строгая). Этот логический оператор представляет собой то же, что и предыдущий, но относится к несоединимым альтернативам. Строгая дизъюнкция - соединение с помощью того же союза двух и более высказываний, которые не могут быть одновременно истинными. Во избежание путаницы мы будем пользоваться для нее словом “либо”. У нас она будет записывается как p 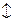 q; читается: p либо q. Иногда эта несовместимость видна непосредственно из самих обстоятельств. Например: потерпевший был ранен либо убит, данный автомобиль “Волга” либо “Москвич”, студенту поставили “отлично” либо “хорошо”. Иногда же это надо специально подчеркивать. “Поеду в отпуск поездом либо самолетом”. Вообще-то может оказаться, что ехать придется и тем и другим транспортом - часть на самолете, часть на поезде. Поэтому в подобных высказываниях надо специально оговаривать, о какой альтернативе идет речь. По истинностным значениям строгая дизъюнкция совпадает с нестрогой во всем за исключением первой строчки. У нее оба простых суждения не бывают одновременно истинными; если же при каких-то обстоятельствах это все же случается, то значит отнесение данной альтернативы к разряду строгих дизъюнкций ложно, что и отмечено цифрой 0 в первой строке колонки для строгой дизъюнкции.
q; читается: p либо q. Иногда эта несовместимость видна непосредственно из самих обстоятельств. Например: потерпевший был ранен либо убит, данный автомобиль “Волга” либо “Москвич”, студенту поставили “отлично” либо “хорошо”. Иногда же это надо специально подчеркивать. “Поеду в отпуск поездом либо самолетом”. Вообще-то может оказаться, что ехать придется и тем и другим транспортом - часть на самолете, часть на поезде. Поэтому в подобных высказываниях надо специально оговаривать, о какой альтернативе идет речь. По истинностным значениям строгая дизъюнкция совпадает с нестрогой во всем за исключением первой строчки. У нее оба простых суждения не бывают одновременно истинными; если же при каких-то обстоятельствах это все же случается, то значит отнесение данной альтернативы к разряду строгих дизъюнкций ложно, что и отмечено цифрой 0 в первой строке колонки для строгой дизъюнкции.
В символической логике нестрогая дизъюнкция используется шире, чем строгая. Поэтому в дальнейшем слово “дизъюнкция” будет означать только нестрогую ее разновидность. Когда же речь пойдет о строгой дизъюнкции, мы будем это специально оговаривать.
Импликация. Она примерно соответствует тому, что в традиционной логике называют условными суждениями, правила для которых в древности начали разрабатывать стоики. Импликация - связь высказываний с помощью логического союза “если..., то”. Общепринятое обозначение - p 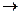 q; читается: p имплицирует (влечет, вызывает) q.
q; читается: p имплицирует (влечет, вызывает) q.
Поскольку условная зависимость не является симметричной, то полезно условиться называть левую от стрелки часть формулы антецедентом, а правую - консеквентом. Надо сказать, в живых языках условные суждения применяются очень широко и с их помощью передается чрезвычайно пестрое разнообразие в оттенках содержания и смысла предложений. Исчисление высказываний учитывает только наиболее типические, преобладающие черты условных связей - прежде всего причинные зависимости. Для более тонкого подхода к ним создаются специальные логические системы, которые называются релевантными. Их изучение не входит в нашу задачу.
Чтобы разобраться с картиной распределения значений истинности импликации в зависимости от разных наборов переменных, воспользуемся опять примером. Пусть нам дано предложение: “Если у Анны сегодня день рожденья, то подарю ей розу”. Здесь логический союз соединяет два высказывания: “Сегодня у Анны день рождения” (p) и “Подарю Анне сегодня розу”(q). Каждое из них может быть как истинным, так и ложным. Само собой понятно, что при истинности каждого из простых высказываний (у Анны в самом деле сегодня день рождения и обещание насчет розы тоже было выполнено) мы посчитаем все сделанное в условной форме заявление истинным: в первой строке колонки импликации (табл. 1) проставлена 1. Но как быть с оценкой такого обещания, когда первое суждение ложно (p=0), а роза тем не менее была подарена (q=1), то есть подарена несмотря на то, что никакого дня рождения Анна сегодня не отмечает? Можно ли считать это отступлением от своих слов? Если и да, то ведь отступление сделано в сторону превышения, оно не обмануло ожидания, наоборот, этим поступком верность данному слову подтверждается еще лучше, чем могла бы. Поэтому при такой комбинации значений переменных правильно будет считать импликативное высказывание истинным. Легко, далее, согласиться, что когда антецедент истинен (p=1), а консеквент ложен (q=0), то высказанное заявление надо признать ложным, ибо это означает, что в день рождения роза вовсе не была подарена. Что касается ситуации, когда день рождения еще не наступил (p=0) и роза пока не подарена (q=0), то при таких обстоятельствах у нас нет никаких оснований считать, что слова расходятся с делами, поэтому импликация в этом случае истинна.
Правда, последнее обстоятельство порождает некоторые не совсем удобные следствия. Формально получается, что любые два ложных предложения, соединенные импликативной связью, образуют истинное высказывание: если дважды два пять, то римский папа магометанин; если коровы квакают, то лягушки доятся. С точки зрения таблицы истинности такие абсурдные утверждения действительно надо признать правильными и истинными высказываниями. Однако в этом не так уж много отступлений от здравого смысла, как это на первый взгляд кажется. В обычной речи такими сочетаниями довольно часто пользуются: если вот эту певицу можно считать артисткой, то тогда вон ту надо признать сказочной сиреной. Вообще надо сказать, что предложения, заявленные в условной форме, почти всегда хотя бы правдоподобны. Обстоятельства, когда они ложны, встречаются сравнительно редко. Скажем, шутливое заявление Виннера: “Если преодолеть технические трудности, то человека можно передавать по проводам”, - будет всегда правильным и бесспорным, хотя и антецедент, и консеквент здесь ложны. Точно так же любой мздоимец может спокойно смотреть в глаза судьям и говорить: “Я взяток не беру, если мне их не дают”. Все утверждение будет правильным, даже если на самом деле каждая его половинка ложна. Недаром древние прорицатели предпочитали делать предсказания в условной форме. Иное из них могло звучать, например, так: “Выиграешь сражение, если не начнешь его первым”. При любом исходе событий возможностей доказывать, что предсказание сбылось, очень много.
Условные предложения очень широко распространены в естественных языках, и все их особенности и смысловые оттенки очень трудно уложить в общие рамки. В логике часто приходится употреблять слово “следовательно”, которое имеет очень много сходства с импликацией, но полностью с ней не совпадает.
Эквивалентность. Она соединяет высказывания логическим союзом “тогда и только тогда”. Наиболее распространенное обозначение эквивалентности p 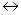 q; читается: p эквивалентно q. Относится она к таким парам явлений и обстоятельств, которые нерасторжимо связаны: есть одно, есть и другое. Допустим, какой-нибудь начальник в министерстве иностранных дел утверждает, что в его отделе каждый сотрудник переходит в дипломаты тогда и только тогда, когда в совершенстве овладевает иностранным языком. Подобно другим, это заявление может быть и истинным и ложным. Давайте посмотрим, как это зависит от значений переменных. Очевидно, что его слова передают то, что есть на самом деле, если их первая и вторая половины - истинные суждения (p=1; q=1). Это значит, что работники, становящиеся дипломатами, знают в совершенстве иностранный язык и каждое из простых высказываний об этом является истинным. И точно также очевидно, что его утверждение ложно, если иные из них переходят на дипломатическую службу, не зная иностранного языка (p=1; q=0), или, наоборот, иностранный язык знают, но в дипломаты попасть не могут (p=0; q=1). При ложности же обоих простых высказываний - и в дипломаты их не переводят, и языка они не знают (p=0; q=0) - слова начальника, конечно, надо оценить как истинные, правильно описывающие сложившуюся в отделе практику.
q; читается: p эквивалентно q. Относится она к таким парам явлений и обстоятельств, которые нерасторжимо связаны: есть одно, есть и другое. Допустим, какой-нибудь начальник в министерстве иностранных дел утверждает, что в его отделе каждый сотрудник переходит в дипломаты тогда и только тогда, когда в совершенстве овладевает иностранным языком. Подобно другим, это заявление может быть и истинным и ложным. Давайте посмотрим, как это зависит от значений переменных. Очевидно, что его слова передают то, что есть на самом деле, если их первая и вторая половины - истинные суждения (p=1; q=1). Это значит, что работники, становящиеся дипломатами, знают в совершенстве иностранный язык и каждое из простых высказываний об этом является истинным. И точно также очевидно, что его утверждение ложно, если иные из них переходят на дипломатическую службу, не зная иностранного языка (p=1; q=0), или, наоборот, иностранный язык знают, но в дипломаты попасть не могут (p=0; q=1). При ложности же обоих простых высказываний - и в дипломаты их не переводят, и языка они не знают (p=0; q=0) - слова начальника, конечно, надо оценить как истинные, правильно описывающие сложившуюся в отделе практику.
Надо помнить, что языковые выражения не всегда соответствуют формальным требованиям. Это заметно и на эквивалентности. Скажем, предложение “Если будешь плохо работать, то будешь уволен” сформулировано как импликативное, но на самом деле оно ближе к эквивалентности. И будет лучше, если мы выразим его именно такой формулой, обозначив составные части, как и раньше, через p и q: p 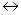 q. В этом можно убедиться, перебрав все варианты для значений переменных. Действительно, при истинности антецедента и консеквента (человек плохо работает и его уволили) сделанное заявление надо, конечно, оценить как истинное. Далее, при ложном антецеденте и истинном консеквенте импликацию надо было бы считать истинной, однако в нашем случае это означало бы признать указанное заявление правильным, несмотря на то, что человек вовсе не работал плохо (высказывание p о его плохой работе ложно), а его все равно уволили (высказывание q о его увольнении истинно). Точнее поэтому будет признать такое выражение эквивалентностью, которая в таком наборе значений переменных является ложной. И третий вариант, когда работника не увольняют (высказывание об увольнении ложно), хотя работает он плохо (высказывание о плохой работе является истинным), тоже подходит к эквивалентности. Наконец, при ложности обоих простых высказываний эквивалентность и импликация образуют истинные высказывания, и это соответствует по смыслу той ситуации, которая взята у нас в качестве примера.
q. В этом можно убедиться, перебрав все варианты для значений переменных. Действительно, при истинности антецедента и консеквента (человек плохо работает и его уволили) сделанное заявление надо, конечно, оценить как истинное. Далее, при ложном антецеденте и истинном консеквенте импликацию надо было бы считать истинной, однако в нашем случае это означало бы признать указанное заявление правильным, несмотря на то, что человек вовсе не работал плохо (высказывание p о его плохой работе ложно), а его все равно уволили (высказывание q о его увольнении истинно). Точнее поэтому будет признать такое выражение эквивалентностью, которая в таком наборе значений переменных является ложной. И третий вариант, когда работника не увольняют (высказывание об увольнении ложно), хотя работает он плохо (высказывание о плохой работе является истинным), тоже подходит к эквивалентности. Наконец, при ложности обоих простых высказываний эквивалентность и импликация образуют истинные высказывания, и это соответствует по смыслу той ситуации, которая взята у нас в качестве примера.
Иногда выражения со словом “чтобы...” тоже могут образовывать эквивалентности. Возьмем для примера высказывание “Чтобы ехать в трамвае, надо купить билет”. Если мы обозначим одну его половину через p, другую - через q и запишем его формулой для эквивалентности, то оно окажется истинным и ложным как раз при таких значениях простых суждений, каковые по смыслу предполагаются во взятом нами высказывании. В некоторых случаях эквивалентностью может быть выражение со словом “для”; например, то же самое высказывание о трамвае и билете мы могли бы сформулировать и с помощью его тоже: “Для поездки в трамвае надо купить билет”.
Введенный таким образом символический язык позволяет превращать в формулы довольно сложные сообщения, составленные из нескольких простых суждений в их самых разных сочетаниях. Так, известная поговорка “Если гром не грянет, мужик не перекрестится” запишется у нас в следующем виде: ( 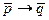 ), где p означает гром гремит, а q - мужик крестится.
), где p означает гром гремит, а q - мужик крестится.
Высказывание о том, что матерью можно стать тогда и только тогда, когда родишь или усыновишь ребенка, потребует трех переменных: p - стать матерью, q- родить ребенка, r - усыновить ребенка. Тогда соответствующая формула будет выглядеть так: ( 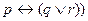 .
.
Возьмем еще несколько выражений, состоящих из трех или четырех простых высказываний, и потом запишем их формулами. Неправда, что наше предприятие получает доход (p) тогда и только тогда, когда не платит налоги ( 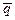 ) или не вносит платежи (
) или не вносит платежи ( 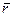 ) :
) : 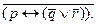
Если его можно назвать преступником (p), то неправда, будто над ним не состоялся суд ( 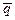 ) и он не был на нем изобличен (
) и он не был на нем изобличен ( 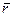 ):
): 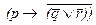 .
.
Если погода окажется не летной ( 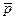 ) и самолет не прилетит (
) и самолет не прилетит ( 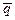 ), то нам придется ехать поездом (r) или плыть пароходом (s):
), то нам придется ехать поездом (r) или плыть пароходом (s): 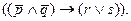
Дата добавления: 2020-06-09; просмотров: 562;











