Основные эквивалентности

Помимо определения истинности сложных составных предложений методы символической логики позволяют также проверять последовательность и определенность мысли, когда она переформулируется в других выражениях. При этом она может оставаться как тождественной самой себе, только высказанной иными словами, так и замененной на другую, вытекающую в качестве следствия из нее. Ключевую роль в этом играет эквивалентность.

В символической логике доказано, что одни логические союзы могут заменяться на другие и при этом не нарушится смысл высказывания. Выражение, содержащее, скажем, союз “или”, можно при желании переформулировать в такое, в котором вместо него будет стоять, скажем, конъюнкция или импликация, и если исходное выражение было истинным, то и полученное в результате преобразования тоже останется истинным. Мы остановимся лишь на самых распространенных видах сложных высказываний - конъюнкции, дизъюнкции и импликации. Они являются также наиболее употребительными и в обычном языке. Доказательство формул для преобразования одних видов суждений в другие очень сложно, мы его опускаем, беря их каждый раз уже готовыми.

Конъюнкция преобразуется в дизъюнкцию с таким же набором значений истинности переменных следующим образом:

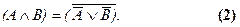
Мы ставим знак равенства между выражениями, подчеркивая этим, что формула не доказана. Но вообще в логике высказываний доказательства этой и других подобных формул даны со всей математической строгостью. Так что при использовании этого закона допустимо ставить знак эквивалентности и применять к нему все законы логики высказываний, подтверждая их, если, надо с помощью нормальных форм (см. выше пар. 1.3). Для преобразования в импликацию надо руководствоваться формулой, которая тоже приводится здесь без доказательства:

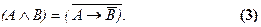
Допустим, у нас имеется сложное конъюнктивное высказывание: “Казак - это пахарь и воин”. Разбив его на два конъюнкта и воспользовавшись приведенными законами преобразования, мы легко получим два высказывания, равносильных исходному, но выраженных иначе - с дизъюнкцией и импликацией: “Неверно, что казак - это или не пахарь, или не воин”, “Неверно, что если казак - пахарь, то он не воин”.

На месте переменных A и B может быть и сложное выражение. Возьмем фразу из комедии «Горе от ума», один из персонажей которой говорит: «Умный человек не может быть не плутом». Придадим ему сначала форму конъюнктивного выражения: «Не бывает, чтоб человек был умен и не был плутом» . Здесь одна переменная имеет отрицание, но указанные законы все равно применимы и в этом случае. 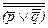Если проводить преобразование по формуле (2), то получится сначала , а потом после применения закона (1) останется :

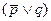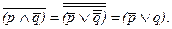
На словах это звучит так: «Или не умен, или плут». А вот как выглядит преобразование по третьей формуле:

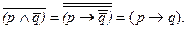
Переведя полученное выражение в словесную формулировку, имеем: «Если человек умен, то он плут».

При переформулировании первоначальных высказываний после их преобразования не всегда возможно оставлять неизменными словесные выражения пропозициональных переменных. В некоторых случаях их приходится существенно менять по соображениям стилистики вплоть до вставки новых слов, не говоря уже о перестановке слов местами. Внешне это выглядит как нарушение фундаментального требования к мышлению: быть определенным - придерживаться одного и того же, однажды выделенного содержания. На деле, однако, нарушений таким образом не вносится, поскольку символическая логика оставляет в рассмотрении, как уже неоднократно подчеркивалось, только семантическое значение предложений и их логические союзы. Лишь они должны оставаться неизменными или, если и меняться, то только в соответствии с законами и правилами для них. Словесная же запись высказываний может меняться. Так что при восстановлении высказывания из формулы, когда оно приняло новую форму в результате преобразований, воспроизводить буквально пропозициональные переменные не приходится. Изменения в них и допустимы, и даже неизбежны. Надо только следить за тем, чтобы они не исказили смысл логических союзов и не повлияли на семантическое значение высказываний.

Для преобразования выражений с тремя переменными возьмем такое сложное высказывание: “Преступление раскрыто, но неверно, что его раскрыли Петров или Сидоров” - 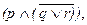где p — “Преступление раскрыто”, q — “Преступление раскрыл Петров”, r —“Преступление раскрыл Сидоров”. Преобразуем его в такое, которое содержит импликацию вместо конъюнкции, для чего нам понадобится воспользоваться законом (3), а скобку 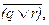мы будем рассматривать как одну переменную (в соответствии с правилом подстановки):

Преобразованное выражение содержит те же переменные, но вместо конъюнкции у него импликация. В новой редакции оно будет звучать уже иначе, чем раньше, хотя и останется тем же самым по смыслу: “Неверно утверждать: если преступление раскрыто, то сделано это Петровым или Сидоровым”.

Дизъюнкция преобразуется в другие выражения по следующим формулам:

,

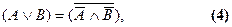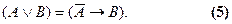
Например, дизъюнктивное высказывание “Преступная группа совершила ограбление вчера (p) или позавчера (q)” будет равносильно такому, выраженному через конъюнкцию: “Неверно, что преступная группа не совершала ограблений ни вчера, ни позавчера”. А высказывание “товар, проходящий через таможню, является экспортным (p) или импортным (q)” может быть преобразовано в равносильное импликативное: “Если товар, проходящий через таможню, не является экспортным, то он является импортным”. Можно также попробовать преобразовать известное латинское изречение: “О мертвых - или ничего, или хорошо”. Сначала напишем формулу для него: 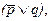где p означает “О мертвых что-нибудь говорить”, q - “О мертвых говорить хорошо”. Преобразование формулы в соответствии с законом (5) пройдет в два этапа:

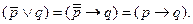
В обновленной формулировке это же изречение получится таким: “Если о мертвых что-нибудь говорить, то хорошо”. Стоит, пожалуй, обратить внимание на то, что при перестановке местами дизъюнктов (“О мертвых - или хорошо, или ничего”) импликативное высказывание звучит иначе: “Если о мертвых не говорить хорошо, то не надо говорить о них ничего”; или еще так: “Если о мертвых не говорят хорошо, то не говорят о них вообще”.

Возможно, конечно, преобразование этого же изречения и в конъюнкцию по формуле (4):

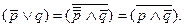
“Hевеpно (неправильно) говорить что-либо о мертвых и при этом не говорить хорошо”.

Импликация. Формулы для перевода импликативных сложных высказываний в иные их виды могут быть получены из предыдущих. Надо только подобрать конъюнктивные и дизъюнктивные выражения, преобразование которых приводит к импликации, не содержащей отрицаний. Попробуем для начала перевести в импликацию конъюнктивное выражение 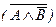по формуле (3).Оно сперва получит вид: 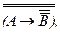а затем упростится за счет нейтрализации двух пар отрицаний: 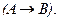Поскольку из взятого нами первоначального выражения в результате эквивалентного преобразования получилась импликация, значит обе эти формулы эквивалентны и мы может записать полученный результат в обратном виде. Получится формула для перевода импликации в конъюнкцию:

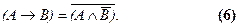
Формула для перевода импликации в дизъюнкцию выводится аналогично.

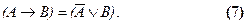
Чтобы проиллюстрировать эти правила преобразования наглядным примером, возьмем широко известное шутливое изречение: “Кому не везет в картах, тому везет в любви”. Обозначив как p — “Везет в картах” и q — “Везет в любви”, получим запись этой мысли с помощью символов: Преобразование ее в конъюнкцию по формуле (7) и дизъюнкцию по формуле (6) проведем одновременно:

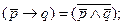
Дизъюнктивное высказывание, эквивалентное первоначальному, будет звучать: “Или везет в картах, или везет в любви”; конъюнктивное - “Не бывает, чтобы не везло в картах и не везло в любви”.

Для проведения таких же преобразований на высказывании с тремя переменными можно взять одно из правил поведения пешехода: “Если переходишь улицу (p), то сначала оглянись направо (q) и налево (r)”. Замена формулы, соответствующей этому утверждению 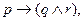потребует обращаться с выражением в скобках как с одной переменной и представляется согласно (6) и (7) в следующем виде:

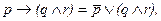
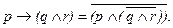
В результате получим заново восстановленные словесные высказывания, эквивалентные разбираемому правилу: “Или не переходи улицу, или сначала оглянись направо и налево”; “Hевеpно переходить улицу и при этом не признавать, что надо сначала оглянуться направо и налево”.

Эквивалентность тоже может быть выражена через другие логические союзы. Суть выражаемой этим союзом связи состоит в том, что одна переменная обуславливает наличие другой, а та в свою очередь свидетельствует о наличии первой. Это может быть выражено двумя импликациями:

Эта формула доказывается в логике высказываний, но мы ее берем без доказательства. При желании можно подсчитать истинностные значения обоих приравненных нами выражений и убедиться, что они у них одинаковы при одних и тех же наборах переменных. Отправляясь от этого правила, можно переводить эквивалентность в другие виды сложных высказываний, если преобразовать далее импликации в конъюнкции и дизъюнкции в соответствии с приведенными ранее формулами. Например:

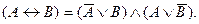
При формулировании законов логики высказываний вместо принятого в ней знака эквивалентности мы использовали знак равенства (=), то есть тот обычный знак равенства, который хорошо знаком каждому со школьных лет. Для нас здесь и в дальнейшем оба знака одинаковы. Обычный математический знак ставится тогда, когда мы не предполагаем применять к эквивалентности правила преобразования ее в другие логические союзы. Не желая прибегать к словесным выражениям, мы будем пользоваться таким символом, дабы подчеркнуть, что распространять на него законы логики высказываний можно только после замены их на принятые в ней знаки. Причем правомерность такой замены должна быть обоснована.

Строгая дизъюнкция может быть выражена с помощью связки конъюнкции, дизъюнкции и отрицания. В логике высказываний соответствующая формула доказывается, мы же только поясним ее. Поскольку этот вид дизъюнктивного высказывания отличается от нестрогой дизъюнкции только тем, что ее альтернативы несоединимы, то, чтобы получить ее из других формул, достаточно добавить к нестрогой дизъюнкции отрицание того, что могут быть одновременно осуществлены одна и другая альтернативы. Тогда значит эквивалентное строгой дизъюнкции выражение должно быть таким:

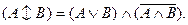
Воспользовавшись формулой для эквивалентной замены конъюнкции (2), полученное выражение можно преобразовать:

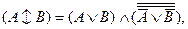
Тогда окончательно правило для преобразования строгой дизъюнкции в другие формулы может быть записано следующим образом:

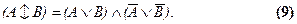
Пояснить данный закон удобно и наглядно с помощью высказывания “Идет либо дождь, либо снег”. Так как выражено оно с помощью союза “либо”, то значит предполагается, что одновременно они не наблюдаются. Тогда значит надо согласиться с тем, что говорит высказывание, образованное из тех же переменных по полученной нами формуле (9): “Идет дождь или снег, но при этом или не идет дождь, или не идет снег”.

С помощью указанных законов и выражающих их формул возможно решение и обратной задачи - проверить равносильность высказываний, когда они составлены из одинаковых простых суждений. Попробуем, например, сопоставить известную поговорку (а) “Любопытство - не порок, но большое свинство” с таким утверждением (б): “Неверно, что если любопытство есть большое свинство, то тогда оно - порок”. Можно ли считать их одной и той же мыслью, только по-разному высказанной, или же они не совпадают? Для ответа надо записать оба высказывания символами:

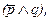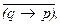(а) (б)

где p означает “Любопытство - порок”, а q - “Любопытство есть свинство”. Теперь осталось только преобразовать либо конъюнкцию в импликацию, либо, наоборот, импликацию в конъюнкцию и посмотреть, получается ли из одной формулы другая или нет. В данном случае проще импликацию превратить в конъюнкцию по формуле (7):

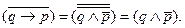
С учетом закона коммутативности конъюнкции получим:

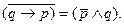
Видно, что полученная формула в точности идентична той, через которую записано конъюнктивное высказывание: “Любопытство - не порок, но большое свинство”. Значит, одно получается из другого в результате преобразования и они, стало быть, эквивалентны.

Попробуем также сопоставить еще два выражения, одно из которых является библейским (а): «Нет власти не от бога» (не бывает, чтобы являлось властью и не было от бога). Другое (б), допустим, звучит так: «Или не власть, или не от бога». Одна это мысль или нет? Чтобы ответить на этот вопрос, надо сначала записать то и другое формулой, а затем привести оба выражения к одному знаку.

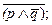(а) (б)

Если мы для преобразования выберем первое выражение, которое является конъюнкцией, и его надо превратить в дизъюнкцию, то нам понадобится формула (2).

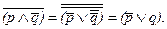
Отсюда видно, что записанное нами дизъюнктивное выражение вовсе не является равносильным первому. На деле, чтобы быть последовательным, надо первое переделывать в такое дизъюнктивное высказывание: «Или не власть, или от бога».

Для преобразования выражения с тремя переменными воспользуемся знакомыми каждому словами из арии о красавице и приписываемых ей склонностях. И запишем их в двух таких выражениях: (а) «Неправда, что или не красавица, или склонна к измене и к перемене»; (б) «Красавица, но неверно, будто склонна к измене и к перемене».

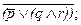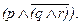(а) (б)

Здесь, как и в предыдущих случаях с тремя переменными, не только одни и те же переменные, но и целая скобка одинаковая в обоих высказываниях. Разница в знаке между этой скобкой и другой переменной. Чтобы сравнить их на равносильность надо привести их к одному знаку именно в этом месте. Допустим, мы возьмемся преобразовывать выражение (а). Но поскольку между скобкой и одиночной переменной дизъюнкция, то выбирать нужную нам формулу, по которой будет происходить преобразование, надо среди (4) и (5). А раз в итоге нам требуется получить конъюнктивное выражение, то значит нужно взять (4).

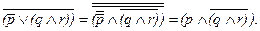
Преобразование показывает, что из первой формулы получается именно вторая, следовательно, оба взятые нами выражения идентичны, в них содержится одна и та же мысль.

Попробуем, далее, выразить сами слова арии как импликацию: «Если красавица, то склонна к измене и к перемене» 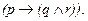И теперь преобразуем, скажем, выражение (2) в импликативное по формуле (6).

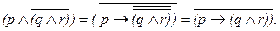
И тогда мы увидим, что оба наши выражения являются прямым отрицанием слов из оперы, потому что после преобразования содержащейся в наших высказываниях мысли в импликацию она будет звучать так: «Неверно, что, если красавица, то склонна к измене и к перемене».