Нуль - единичная проверка истинности высказываний

Принятая в логике высказываний символика позволяет существенно расширить сведение мыслительных операций к простому счету. При желании их можно передать таким способом даже вычислительным машинам. Надо только научиться вычислять истинностное (семантическое) значение сложных высказываний, записанных в виде формулы (мы будем называть их далее также пропозициональными функциями). Каждое из простых высказываний, как мы помним, может принимать два возможных значения: “истинно” или “ложно”, и в зависимости от семантического значения переменных составленные из них сложные сообщения будут принимать разные значения. Так, приведенное выше высказывание о получении доходов при уклонении от уплаты налогов и платежей может (как, впрочем, и остальные из тех же высказываний при различных конкретных обстоятельствах) быть как истинным, так и ложным, причем это относится и к каждому компоненту в отдельности, и к формуле в целом. Предприятие может на самом деле получать доход (p=1) и при этом не уплачивать налоги (q=0) и не вносить платежи (r=0). Но оно может и не получать в действительности доход при тех же условиях. Сверх этого, существуют еще и другие возможные сочетания действительных обстоятельств, которые можно выразить через комбинацию семантических значений пропозициональных переменных. В каждом случае мы, разумеется, будем по-разному оценивать выраженное формулой заявление - соответствует оно действительности или нет, являются ли истинными слова о получении доходов отмеченным путем или их надо признать ложными.

Определение семантического значения той или иной формулы через истинностные значения входящих в нее пропозициональных переменных называется разрешением (решением) формулы. Оно составляет очень важную задачу в исчислении высказываний. Если бы символическая логика обходилась только простейшими пропозициональными функциями, образуемыми перечисленными в предыдущем разделе союзами, то вся задача решалась бы каждый раз просто: у всех их за исключением отрицания имеется только четыре варианта сочетания разных по значению пропозициональных переменных (а у отрицания и того меньше - два). Все они приведены в таблице истинности, достаточно заглянуть туда и найти соответствующую строку.

Дело, однако, существенно усложняется, когда формула содержит более или менее сложное сплетение таких элементарных функций. Простое обращение к таблице истинности здесь уже не помогает. Существует несколько способов, позволяющих устанавливать, истинно или ложно выражение при разных наборах значений пропозициональных переменных. Наиболее простым и удобным является метод нуля и единицы.

Возьмем какое-нибудь конкретное высказывание, допустим, такое: “Если получу стипендию, то куплю себе учебник по логике, и если не получу стипендию, то учебник по логике покупать не стану”. Обозначим через p простое высказывание “Получу стипендию” и через q - “Куплю учебник по логике”. Тогда формула для этого выражения будет выглядеть так:

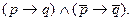
Предположим, далее, что на самом деле учебник не был куплен, хотя стипендия была получена. На языке символической логики это означает, что высказывание p является истинным (p=1), а высказывание q - ложным (q=0). В данном случае само собой понятно, что сделанное заявление о покупке учебника при получении стипендии не соответствует реальным делам, следовательно, ложно. Но нам надо получить этот результат с помощью подсчета (так, чтобы к нему могла бы прийти и машина). Для разрешения данной формулы надо сначала подставить в нее вместо буквенных переменных их цифровые значения. Тогда получим:

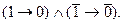
Теперь надо поэтапно упрощать выражение. Сначала проведем отрицания внутри скобок, остальную же часть формулы пока просто перепишем без изменений. Поскольку в таблице истинности отрицание обозначено как p, то для вычисления выражения 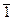надо найти в столбце для p ту строку, где стоит 1 (первая строка), и найти после этого цифру, которая ей соответствует в столбце 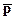. В этом месте находится нуль: отрицание истинного высказывания дает высказывание ложное. Значит, отрицание единицы можно заменить на нуль.

Аналогично отрицание нуля можно заменить на единицу:

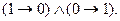
Следующим шагом мы должны вычислить две импликации. Левой из них в колонках для p и q соответствует третья строка, и импликация в этой строке является ложной (там стоит цифра нуль); значит выражение 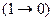можно заменить на 0. Для правой берем вторую строку; в колонке импликации на ней стоит цифра 1. Значит выражение 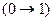можно заменить на 1. Тогда формула сведется к конъюнкции, которая легко вычисляется аналогичным образом и заменяется на нуль:

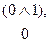
Если выразить все преобразование одной строкой, то оно будет выглядеть так:

.

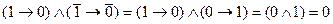Получается, вся эта формула при данных значениях переменных содержит ложное высказывание. Это надо понимать так: автор высказывания о покупке учебника после получения стипендии на самом деле не сдержал своего слова. Мы могли бы проверить истинность его намерения и при других значениях переменных. Поскольку их всего две, то возможных наборов четыре - столько же, сколько и у простых функций. Результаты сведены здесь в табл. 2.

Таблица 2

p	q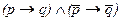

Из нее видно, что если бы высказывание сопровождалось приобретением учебника, несмотря на то, что стипендия не была получена (вторая строка), то его слова надо было бы признать не соответствующими делам. В то же время его высказывание является истинным, если стипендии не было и учебник не был куплен (последняя строка). Тем более его высказывание не является ложным, если после получения стипендии учебник был куплен. Легко увидеть, вникнув в содержание всего заявления, что именно так мы и сами оценили бы его истинность при всех перечисленных вариантах реальных обстоятельств.

Возьмем еще такую ситуацию в качестве примера. Предположим, руководитель предприятия заверяет своих коллег: «Неправда, будто мы или получим льготный кредит, или не достроим новое здание». И допустим, далее, что кредит был получен, а здание достроено. Спрашивается, сказал ли он правду? Обратимся к методу нуля и единицы. Формула, выражающая его слова, должна представлять собой отрицание нестрогой дизъюнкции, причем с одной ее стороны переменная, с другой – переменная с отрицанием: 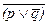, p – «Получен льготный кредит», q – «Достроено новое здание». Так будет выглядеть записанная в виде формулы информация руководителя. Сами же действительные обстоятельства запишутся в виде значений пропозициональных переменных: оба простых высказывания истинны (p=1, q=1).

Подставим, как и прежде, в формулу вместо переменных их числовые значения и проводим поэтапное вычисление:

.

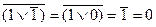Ноль говорит о том, что слова руководителя не соответствуют тому, что произошло на самом деле, то есть его слова ошибочны или ложны. Вычисление других возможных значений формулы и их интерпретацию предоставляется выполнить самостоятельно. Результаты можно сверить по приведенной здесь табл. 3.

Таблица 3

p	q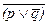

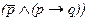
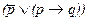
Подобным образом можно вычислять семантические значения любых формул, как бы они ни были сложны. Причем, если переменных больше двух, то тогда, разумеется, и вариантов их сочетаний больше: при трех - 8, при четырех - 16 и т.д. Исчисление высказываний обеспечивает, таким образом, как и правила традиционной логики, последовательность в выводах и рассуждениях. Однако в отличие от аристотелевской логики здесь речь может идти о последовательности не только в словах и мыслях, но также и о последовательности в делах: в самом ли деле высказанные заявления соответствуют тому, что осуществлено на практике, и соответствует ли описанная в высказывании картина каких-либо обстоятельств тому, что имеет место в действительности.

Надо, однако, помнить, что исчисление высказываний - первый шаг в становлении символической логики. В нем пока еще много несовершенного. Раньше уже говорилось об упрощении действительной мысли в отрицаниях и импликациях. А когда их несколько в одной достаточно большой формуле, то дело может доходить и до нелепостей. Громоздкие формулы для целей выражения мысли из-за этого ненадежны.

Одна и та же формула описывает множество разных по содержанию высказываний. Так, предложение “Если встречу Катю, то пойдем с ней в кино или в театр” запишется в виде следующего буквенного выражения: 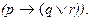В то же время можно привести и множество других высказываний, которые запишутся с помощью этой же самой формулы. Например: “Если дверь открыта, значит, дома брат или сестра”, “Если электросчетчик работает, значит, включена плита или телевизор”, “Если покупка – мороженое, то она стоит восемь или десять рублей”, “Если политик выполнит обязательства, то понизятся цены или возрастет зарплата”. Формула передает только то общее, что характерно для всех приведенных примеров, поскольку, как мы помним, высказывание оставляет от суждения только одно свойство - быть либо истинным, либо ложным. Все остальное выпадает из рассмотрения. Истинностные значения остаются, разумеется, неизменными при одних и тех же сочетаниях значений переменных, какое бы содержание в них ни вкладывалось. Причем, заметьте, самое первое из взятых нами высказываний не допускает, если подумать над его смыслом, чтобы при ложности p были истинными q и r (p=0, q=1, r=1); между тем формула может быть вычислена и при этих значениях тоже и даже окажется истинным высказыванием. Это значит, что встреча с Катей не получается, но выход с ней в театр и кино состоится.

Такая несуразица возникла, однако, не из-за несовершенства языка символической логики, так как данный вариант не является ложным (для других высказываний из того же набора полученное сочетание вполне допустимо). Он невыполним вообще. Чтобы его избежать, надо было воспользоваться более сложным выражением, скажем, таким: “Если встречу Катю, то пойдем с ней в кино или в театр, и, если не встречу Катю, то не пойдем ни в кино, ни в театр”. Соответствующая формула будет выглядеть так: 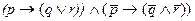. При тех же значениях переменных, которым соответствуют недопустимые по самой сути дела стечения обстоятельств, она образует ложное высказывание.

Язык символической логики позволяет обнаруживать некоторые трудно уловимые нюансы в нашей речи. Возьмем высказывание: “Он мухи не обидит, а если и обидит, то прощения попросит”. Формула для него запишется таким образом: 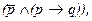а семантические значения можно видеть в помещенной выше табл. 3. Подобными выражениями мы обычно характеризуем обходительных людей, и если в общении с ними столкнемся со случаем, когда такой человек все же доставил кому-то неприятности (p=1), но тут же принес извинения (q=1), то мы, видимо, подумали бы, что такое поведение подтверждает данную ему характеристику. Однако, взявшись просчитать формулу при отмеченных значениях переменных, мы обнаружим, что она, как ни странно, дает ноль (см. табл. 3), т.е. слова о нем не соответствуют его поступкам. Однако все станет понятно, стоит лишь переставить местами слова в высказывании: “Если он обидит хотя бы только муху, то попросит прощения, но вообще-то он никого не обидит”. Формула для обновленного выражения остается той же самой, ибо последовательность изложения не имеет принципиального значения. Просто в такой формулировке меняются акценты. В высказывании одна половина категорически заверяет, что данный человек вообще никого не обижает, а другая половина фразы всего лишь усиливает это убеждение, т.е. данное выражение в действительности означает, что характеризуемый так человек вообще не наносит обиды кому бы то ни было, поэтому и подсчет дал не тот результат, который ожидается интуитивно. На деле анализируемая формулировка некорректна; правильнее использовать вместо союза «и» союз «или» между скобкой и переменной: “Он или не обидит даже мухи, или, если и обидит, то попросит прощения” 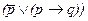. Таблица 3 показывает, что данная характеристика будет точнее передавать обходительный образ действий, если ее выразить именно таким способом.

Формулами можно выражать также и договорные отношения и затем проверять, были ли они выполнены в тех или иных обстоятельствах. Скажем, транспортная организация могла бы заключить такой договор: «Если действует железнодорожное сообщение, а груз задерживается, то фирма уплачивает штраф» 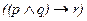, p – «Действует железнодорожное сообщение», q – «Груз задерживается», r – «Фирма уплачивает штраф». Зависимость истинностного значения такой формулы от набора переменных показана в табл. 4. Из нее видно, что при функционирующем транспорте, задержанном грузе и уплаченном штрафе (p=1, q=1, r=1) формула дает значение “истинно”, иными словами, договорные обязательства будут соблюдены. А если в тех же условиях штраф не уплачен (p=1, q=1, r=0), то просчет формулы дает значение “ложно”, стало быть, договор окажется нарушен. Это, разумеется, соответствует интуитивным ожиданиям, но, обратите внимание, что других нарушений такого договора вообще, оказывается, нет (при всех остальных наборах переменных - только единица). Так что даже если транспорт не действует, груз не задержан, а штраф тем не менее уплачен (p=0, q=0, r=1), договор надо считать все же соблюденным, хотя это явная нелепость.

Таблица 4

p	q	r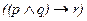

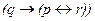
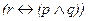
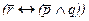
Дело здесь в тех особенностях импликации, о которых ранее говорилось. Ее консеквент содержит следствие, которое может вызываться не только явлением или действием, указанным в антецеденте, но и многими другими, совершенно посторонними обстоятельствами. Поэтому для определения соответствия действий сторон договорным обязательствам надо просчитывать каждый раз два варианта: штраф уплачен и штраф не уплачен. В данном случае окажется, что нести штрафные санкции нет необходимости в том смысле, что договорные обязательства будут выполнены как при уплате штрафа, так и при неуплате. Могут быть также формулировки, в которых в случае уплаты и не уплаты договор не выполняется. Кроме того, можно придумать и более корректное выражение: «Если груз задерживается, то фирма платит штраф тогда и только тогда, когда действует железнодорожное сообщение» 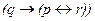. Оно точнее предыдущего (см. табл. 4), но и здесь при отдельных сочетаниях обстоятельств, например транспорт не действовал, но груз не задержан (p=0, q=0), недвусмысленная оценка выполнения или невыполнения обязательств по договору получается лишь через двойной просчет формулы.

Допустимо также вместо импликации использовать эквивалентность. Тот же самый договор звучал бы тогда так: «Фирма уплачивает штраф тогда и только тогда, когда железнодорожное сообщение действует, а груз задерживается» 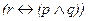. В таком выражении договора двойной подсчет не требуется нигде, так как при соблюдении всех условий формула дает значение «истинно», а при несоблюдении – «ложно» (см. табл. 4). Но и здесь имеются свои тонкости. Если бы нам вздумалось те же условия выразить в отрицательной форме, то, как ни странно, получится немало самых настоящих нелепостей. В самом деле, выразим те же условия в таком виде: «Фирма не уплачивает штраф тогда и только тогда, когда железнодорожное сообщение не действует и груз задерживается» 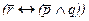. Казалось бы, это та же самая мысль, только выражена она иначе. Тем не менее из той же таблицы видно, что совпадение с предыдущей формулой имеет место лишь отчасти. Причем если бы транспорт не действовал, но груз не задержался, а фирма все же уплатила штраф, то так сформулированный договор был бы соблюден, и наоборот, если бы она не уплатила штраф, то это означало бы нарушение договорных условий. На самом деле, чтобы зафиксировать договорные условия в отрицательной форме, надо воспользоваться формулой 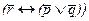, которая на словах выражается так: «Фирма не уплачивает штраф тогда и только тогда, когда или железнодорожное сообщение не действует или груз не задерживается». Ее цифровые значения при любых наборах переменных полностью совпадают с той корректной формулой из табл. 4, для которой, как было отмечено, не требуется двойного просчета.

В общем-то тут надо помнить как о недостатках естественного языка, так и несовершенстве языка логики высказываний. Дальнейшие уточнения таких вопросов здесь были бы излишними. Достаточно отметить, что без символической логики, возможно, мы не заметили бы таких тонких зависимостей в смыслах предложений.

Нормальные формы

Метод нуля и единицы удовлетворительно работает, пока дело касается формул, содержащих не более трех-четырех переменных. Однако, когда их число возрастает, применение этого метода существенно осложняется: при шести переменных таблица истинности формулы состоит из 64 строк, при 10 она уже разрастается до 1024. Между тем, теория должна располагать методикой, позволяющей определять семантические значения в принципе даже при неограниченном числе переменных. Приходится поэтому искать дополнительные методы разрешения. К числу таковых относится сведение к так называемым нормальным формам[[Если этот раздел покажется трудным, то его можно не изучать. На уяснение последующего материала это не повлияет.]. Когда это достигается, то тогда по одной лишь структуре формулы удается определить ее семантику. Правда, при этом устанавливается только тип формулы: дает ли она при всех наборах переменных только истинные высказывания или только ложные, или среди них есть то и другое.

Нормальные формы составляются из так называемых элементарных конъюнкций и дизъюнкций. В формулах, приведенных к нормальным формам, других логических союзов, кроме указанных, нет; отрицания допускаются только над переменными. Если исходная формула содержит иные знаки, а также отрицания над выражениями или скобками, то тогда ее сначала надо избавить от всего этого, применив так называемые эквивалентные замены. О таких заменах речь будет впереди.

К элементарным конъюнкциям относятся выражения вида

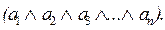
Здесь под a_i понимается любое высказывание.

Так, формула 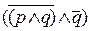не является элементарной конъюнкцией, поскольку в ней есть отрицание над скобкой. Элементарная конъюнкция допускает отрицания только над переменными. Примечательной особенностью таких формул является то, что содержащаяся в них мысль может быть истинной только при условии, что все до единого простые суждения, совокупность которых ее выражает, являются истинными; достаточно вставить хотя бы один ложный конъюнкт, и все выражение станет обязательно ложным, сколько бы там ни содержалось помимо него истинных высказываний в качестве конъюнктов. Причем в такой интерпретации элементарных конъюнкций нет никакой натяжки или упрощения. В практической деятельности мы именно так и относимся к какой-либо информации, если она изложена как соединение через союз “и” нескольких предложений. Допустим, у нас имеется утверждение: “Вводится дополнительный налог на импорт изделий из стекла, хрусталя, фарфора, фаянса, майолики”. И если бы включение сюда, скажем, майолики оказалось неправильным, то значит всю информацию надо было бы признать ложной. Не в том, конечно, дело, что ложность в одном пункте превращает и остальные в ложные. Нет, каждое в отдельности суждение может оставаться истинным, однако вся информация в целом содержит изъян, следовательно, может из-за этого порождать ошибки. В этом смысле и только в этом, то есть взятое целиком, а не в отдельных своих компонентах, сложное конъюнктивное высказывание является ложным, когда ложным оказывается хотя бы один из его простых составляющих.

Отсюда вытекает очень важное в практическом отношении следствие: к элементарной конъюнкции можно присоединять неограниченное число истинных высказываний, а также можно их из нее убирать. Семантическое значение формулы не изменится, оно будет определяться теми конъюнктами, которые имелись в ней до введения или остались после удаления какой-то части: есть среди них хоть один ложный конъюнкт - все выражение ложно, нет - оно истинно. Это можно записать в виде такой формулы:

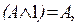
где 1 представляет собой любое истинное высказывание или формулу, среди множества семантических значений которой имеется только одно - “истина” и нет другого.

И еще одно не менее примечательное свойство: когда в элементарной конъюнкции содержится хотя бы одна пара, состоящая из переменной и ее отрицания, то тогда вся формула при любых значениях переменных образует только ложные утверждения. Это нетрудно понять, так как в этом случае в ней обязательно имеется хотя бы одна переменная, имеющая значение “ложь”. А этого, как уже сказано, достаточно, чтобы и вся формула образовывала только ложные высказывания.

Элементарные дизъюнкции строятся подобным же образом (переменная a_i тоже означает любое высказывание):

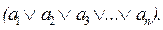
В отличие от элементарных конъюнкций эти формулы могут быть ложными только тогда, когда ложны абсолютно все их дизъюнкты. И это соответствует употреблению таких высказываний в обиходе и науке. Допустим, кто-нибудь сообщает нам, что некий переводчик владеет то ли китайским, то ли японским, то ли корейским, то ли вьетнамским языком. Поскольку перечисляются возможные альтернативы, то достаточно назвать хотя бы один и только один язык, который он на самом деле знает, и все равно такая информация не собьет нас с толку. Пусть даже потом перечисляются десятки языков, которые данному переводчику в действительности неизвестны. По этой причине к элементарной дизъюнкции можно прибавлять любое число ложных выражений, ее истинность все равно будет определяться теми дизъюнктами, которые были до этого: есть среди них хоть один истинный - все сложное высказывание будет истинным, нет такого - будет ложным. И можно также отбрасывать заведомо ложные. Следовательно, для нее будет правильно написать такой закон:

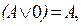
где 0 - ложное высказывание или формула, дающая только ложные высказывания.

Наличие в элементарной дизъюнкции хотя бы одной переменной вместе с ее отрицанием приводит к тому, что в ней всегда обязательно содержится как минимум одна переменная со значением “истина”. Поэтому такая формула обязательно будет давать только истинные высказывания, какие бы наборы переменных мы ни брали.

Конъюнктивная нормальная форма (КНФ). Из элементарных конъюнкций и дизъюнкций составляются нормальные формы, которые делятся на две разновидности: конъюнктивные и дизъюнктивные. Конъюнктивная нормальная форма представляет собой выражение вида

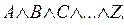
где A, B, C, ...Z являются элементарными дизъюнкциями. Она, как видим, сходна с элементарной конъюнкцией, но каждый конъюнкт в свою очередь представляет собой элементарную дизъюнкцию. Так, формула

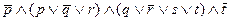
представляет собой конъюнктивную нормальную форму (КНФ).

Любая формула логики высказываний может быть приведена к КНФ. Правда, процесс сведения не относится к числу легко осуществимых для тех, кто не имеет навыка работы с математическими формулами. Зато с помощью конъюнктивных нормальных форм легко определить тип формулы. Если в каждой элементарной дизъюнкции встречается хотя бы одна переменная с ее отрицанием, это означает, что все члены конъюнктивной нормальной формы образуют только истинные высказывания и никакие другие. Следовательно, и все выражение в целом, из которого получена данная КНФ, также дает только истинные высказывания. Дальнейшая проверка истинностных значений формулы становится излишней.

Дизъюнктивная нормальная форма (ДНФ). Сочетание элементарных конъюнкций, соединяемых с помощью дизъюнкции, образует дизъюнктивную нормальную форму:

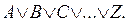
A, B, C,... Z - элементарные конъюнкции. Так, к дизъюнктивным нормальным формам относится такая формула:

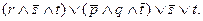
К ДНФ также может быть сведено любое выражение, и если в каждой элементарной конъюнкции находится хотя бы одна пара, состоящая из переменной и отрицания, то тогда каждый дизъюнкт в ДНФ ложен и, следовательно, вся формула образует только ложные высказывания.