Теорема Лапласа (интегральная)
Вероятность того, что в п независимых испытаниях, в каждом из которых вероятность появления события равна Р(0 < р < 1) , событие наступит не менее k1 не более k2 раз, т.е.
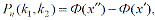 (3.23)
(3.23)
где 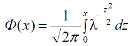 - функция Лапласа;
- функция Лапласа;
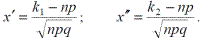
Пример.Случайные значения времени работы t очистного комбайна между отказами подчиняются экспоненциальному закону распределения. Средняя наработка на отказ комбайна То = 19 ч. Требуется определить вероятность безотказной работы Р(t) комбайна для шестичасовой рабочей смены (t = 6 ч) и вероятность попадания СВ в интервалa 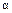 = 9 ч;
= 9 ч; 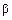 = 19 ч.
= 19 ч.
По формуле (3.11), приняв t = 6 ч и mt= T0=1=9 ч, получим
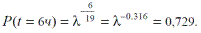
По формуле (3.13):
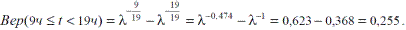
Пример.Средняя наработка до отказа элементов горной машины, теряющего работоспособность по причине изнашивания составляет Т1= 1200 ч, случайные величины наработки до времени ti подчиняются нормальному закону распределения. Коэффициент вариации Vt = 0,35. Рассчитать P(t) для t = 300 ч и вероятность попадания СБ на интервале с границами 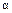 = 1000 ч и
= 1000 ч и 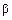 = 2000 ч.
= 2000 ч.
По формуле (3.16)
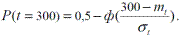
Приняв mt= T0=1=1200 ч и 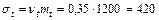 , получим
, получим
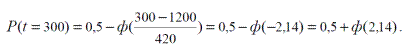
Согласно табл. П1 приложения В для z = 2,14 ф(z) = 0,484.
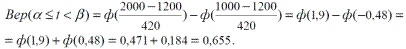
Дата добавления: 2020-05-20; просмотров: 726;











