Законы дискретных распределений случайной величины
Для дискретных случайных величин функция распределения имеет вид:
F(x) = SP(X=xi), (3.28)
где xi – значения случайной величины;
Р – вероятности появления данного значения.
Когда текущая переменная х проходит через одно из возможных значений дискретной величины Х, функция распределения меняется скачкообразно, причем величина скачка равна вероятности этого значения. Сумма всех возможных скачков функции F(x) равна единице. График функции распределения дискретной случайной величины представляет собой ступенчатую кривую (рис. 3.1, б)
В задачах надежности из дискретных распределений наиболее часто используют биномиальное распределение и распределение Пуассона.
Биноминальным называют закон распределения дискретной случайной величины числа х появления событий K раз в n независимых испытаний, в каждом из которых вероятность появления событий равна Р.
Вероятность того, что событие наступит ровно K раз (безразлично, в какой последовательности) определяется по формуле Бернулли:
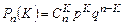 (3.29)
(3.29)
или
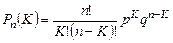 , (3.30)
, (3.30)
где q = 1 – p – вероятность непоявления события в каждом испытании.
Если число испытаний n велико, а вероятность появления событий р в каждом испытании мала, то используется формула
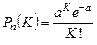 , (3.31)
, (3.31)
где а = np – среднее число (математическое ожидание) событий в n испытаниях.
Распределение дискретной случайной величины Х, описываемое последней формулой, называется распределением Пуассона.
Биноминальное распределение имеют, например, отказы восстанавливаемых объектов в течение заданного периода времени.
Пример. На шахте работают шесть конвейеров с турбомуфтами. Вероятность безотказной работы одной турбомуфты в течение четырех месяцев q = 0,8. Найти вероятность выхода из строя в течение четырех месяцев нуля, одной, двух, трех и четырех муфт:
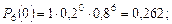
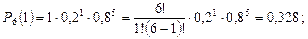
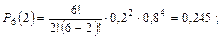
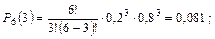
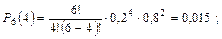
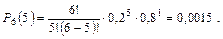
Пример. Цепь скребкового конвейера СП-63 имеет n = 200 соединительных звеньев. Вероятность выхода из строя соединительного звена в течение суток р = 0,01 (q = 1 – 0,01 = 0,99). Определить вероятность порыва в течение суток четырех звеньев:
А = nр = 200 × 0,01 = 2;
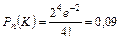 .
.
Вероятность порыва в течение суток больше четырех звеньев
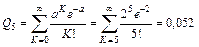 .
.
Дата добавления: 2020-05-20; просмотров: 815;











