Наивероятнейшее число наступлений события

Число К_о (наступления событий в независимых испытаниях, в каждом из которых вероятность появления событий равна р) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k раз, превышает или не меньше вероятности остальных возможных исходных испытаний. Наивероятнейшее число К_о определяется из двойного неравенства

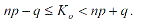(3.24)

Причем если часть выражения пр-q дробное, то существует одно наивероятнейшее число К_о. Если пр-q целое, то существует два наивероятнейших числа К_о и К_о+1; если число пр целое, то наивероятнейшее число К_о = пр.

В тех случаях, когда вероятность Р появления события А из опыта к опыту меняется, определение вероятности появления события А ровно k раз из группы п независимых опытов производится на основании общей теоремы о повторении опытов

(3.25)

т.е. искомая вероятность равна сумме всех возможных произведений, в которых р с разными индексами входит k раз, а q с разными индексами(п - k) раз. Для того чтобы чисто механически составлять все указанные возможные произведения, используют производящую функцию.

Производящей функцией вероятностей Р_п(k) называют функцию, определяемую равенством

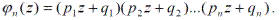(3.26)

Вероятность Р_п(k) того, что в п независимых испытаниях, в первом из которых вероятность появления события А равна р₁, во втором р₂ и т.д., событие появляется ровно k раз, равна коэффициенту при z^k в разложении производящей функции по степени z .

Например, при п = 2

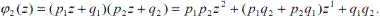
Здесь коэффициент p₁p₂при z² равен вероятности p₂(2) того, что в двух испытаниях событие А появиться 2 раза, коэффициент р₁q₂ + p₁q₂при z¹ равен вероятности p₂(1) того, что событие А появиться 1 раз, коэффициент при z⁰ , т.е. свободный член q₁q₂равен вероятности p(0) того, что событие А не появиться ни одного раза.