Теорема полной вероятности
Теорема полной вероятности формируется на основании теорем сложения и умножения вероятностей.
Пусть сложное событие A может произойти только с осуществлением n некоторых других несовместных событий - предположений, называемых гипотезами Hi, образующими полную группу несовместных событий H

(3.13)
Событие A может осуществиться, если произойдет одно из следующих парных событий: Hi с вероятностью P(Hi) и A/Hi с вероятностью P(A/Hi). Вероятность появления события A определяется по формуле полной вероятности

(3.14)
Пример.Требуется определить вероятность отказа секции механизированной крепи qс за время работы t, если вероятности независимых отказов qi ее элементов: гидростоек (ГС), гидроцилиндров передвижки (ГП), металлоконструкции (МК) и блока управления секцией (БУ) составляют для времени t соответственно:
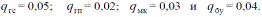
Дадим понятие события «отказ секции крепи». Секция крепи откажет, если откажут: гидростойка или гидроцилиндр передвижки, или металлоконструкция, или блок управления, или гидростойка и гидроцилиндр, или гидростойка и металлоконструкция и т. д.
Поэтому для рассматриваемого события следует, что для расчета вероятности отказа qс секции механизированной крепи следует использовать теорему сложения вероятностей для совместных событий, а для определения вероятности безотказной работы теорему умножения вероятностей для независимых событий.
Таким образом:
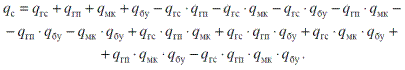
Подставим вместо qi их величины, получим
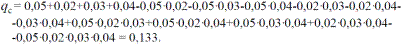
Для решения поставленной задачи может быть применена теорема умножения вероятностей для независимых событий. Событие «безотказная работа» секции крепи Рс за время t осуществляется, если безотказно будут работать ГС, ГП, МК и БУ, тогда
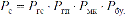
Поскольку отказ и «безотказная работа» секции крепи – события
противоположные, то величины 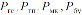 могут быть найдены по заданным значениям
могут быть найдены по заданным значениям 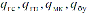 , а именно
, а именно
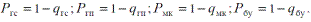
В итоге получаем
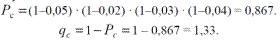
Формула Бейеса
Теорема гипотез является следствием теоремы умножения и формулы полной вероятности.
Имеется полная группа несовместных гипотез 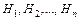 . Известны до опытные вероятности этих гипотез
. Известны до опытные вероятности этих гипотез 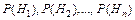 . Известны также условные вероятности P(A/Hi). сложного события А, которое может появиться вместе с одной из гипотез Нi.
. Известны также условные вероятности P(A/Hi). сложного события А, которое может появиться вместе с одной из гипотез Нi.
Производится опыт, в результате которого произошло событие А, но неизвестно, вместе с какой из гипотез Нi осуществилось это событие. В этом случае значения условных после опытных вероятностей гипотез P(Hi/A) определяется по теореме гипотез:

(3.15)
Пример. При работе очистного механизированного комплекса, состоящего из выемочной машины – В, доставочной машины – Д, и крепи - К в разные моменты смены согласно технологии горных работ могут функционировать одна или несколько машин одновременно. Гипотеза Н1 – функционируют три машины В, Д , К ; гипотеза Н2 –функционируют Д и К ; гипотеза Н3 – функционирует только крепь К. Обычно В, Д и К функционируют 40% времени смены, т.е. P(H1)=0,4; Д и К –5% времени т.е. P(H2)=0,05; К – 55% времени т.е. P(H3)=0,55.
Условные вероятности появления опасных отказов оборудования (события А) соответственно равны: P(A/H1)=0,03; P(A/H2)=0,02; P(A/H3)=0,01.
Требуется определить условную вероятность P(H1/A) и вероятность 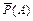 события A (непоявления опасного отказа) в любой момент смены.
события A (непоявления опасного отказа) в любой момент смены.
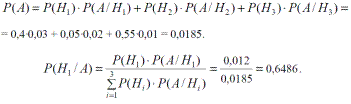
Повторение опытов
В теории надежности приходится встречаться с задачами, в которых один и тот же опыт повторяется неоднократно. В результате каждого опыта может появиться или не появиться некоторое событие А. При этом интерес представляет не результат каждого отдельного опыта, а общее число появления события А. Такие опыты называются независимыми относительно события А.
Когда при проведении п независимых опытов вероятность Р появления события А во всех опытах одна и та же, то вероятность того, что событие А наступит, ровно k раз, не менее k раз, более k раз, и не более k раз, может быть определена по формуле Бернулли и теоремам Лапласа.
Формула Бернулли
Вероятность того, что в п независимых опытах, в каждом из которых вероятность появления события Р(0≤р≤1) , событие А наступит ровно k раз (безразлично в какой последовательности).
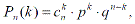 (3.16)
(3.16)
или
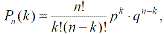 (3.17)
(3.17)
где q=1-p.
Вероятность того, что событие наступит:
- менее k раз
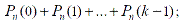 (3.18)
(3.18)
- более k раз
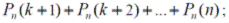 (3.19)
(3.19)
- не менее k раз
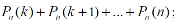 (3.20)
(3.20)
- не более k раз
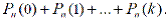 (3.21)
(3.21)
Пример.Требуется рассчитать вероятность появления равно 0, 1, 2, 3 и 4-х отказов секций механизированной крепи в четырех (п = 4 ) независимых опытах (рабочих сменах) секции механизированной крепи, если вероятность отказа секции qc(t = 6ч) = 0,133, а вероятность безотказной работы Рс (t = 6ч) = 1- qc (t = 6ч) = 0,867.
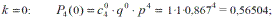
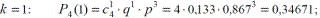
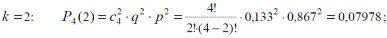
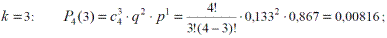
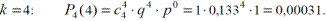
При этом 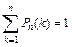 , что и подтверждают полученные результаты расчетов.
, что и подтверждают полученные результаты расчетов.
- менее k раз
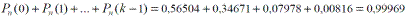
- не менее k раз
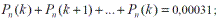
- не более k раз
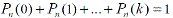
Дата добавления: 2020-05-20; просмотров: 736;











