Давление Лапласа. Капиллярные явления
|
 1. Давление Лапласа. Кривизна поверхности жидкости приводит к изменению внутрижидкостного давления. Чтобы его определить, выделим на поверхности капли малый элемент в форме криволинейного параллелограмма ABCD площадью S (рис.63).
1. Давление Лапласа. Кривизна поверхности жидкости приводит к изменению внутрижидкостного давления. Чтобы его определить, выделим на поверхности капли малый элемент в форме криволинейного параллелограмма ABCD площадью S (рис.63).
Здесь R1 и R2 – радиусы кривизны поверхности в двух взаимно перпендикулярных направлениях MN и KL.
 По касательной к поверхности перпендикулярно сторонам AD и BC действуют равные по величине силы поверхностного натяжения
По касательной к поверхности перпендикулярно сторонам AD и BC действуют равные по величине силы поверхностного натяжения 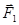 и
и 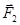 . Разложим эти силы на две составляющие. Одна – нормальная к поверхности в точке O, а другая – касательная к поверхности в этой же точке.
. Разложим эти силы на две составляющие. Одна – нормальная к поверхности в точке O, а другая – касательная к поверхности в этой же точке.
Касательные составляющие в сумме дают нуль, а составляющие вдоль нормали OO1 направлены в одну сторону. Найдем их сумму.
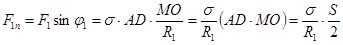 . (18.1)
. (18.1)
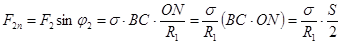 . (18.2)
. (18.2)
Аналогично находятся составляющие сил 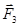 и
и 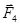 .
. 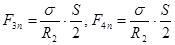 . (18.3)
. (18.3)
Складываем. 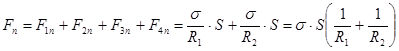 . (18.4)
. (18.4)
Разделив эту силу на площадь S, получаем давление, создаваемое внутри жидкости ее искривленной свободной поверхностью. 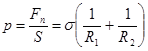 . Пьер Лаплас, 1806 (18.5)
. Пьер Лаплас, 1806 (18.5)
Эту формулу впервые получил Лаплас в 1806 г., и поэтому ее часто называют законом Лапласа: внутрижидкостное давление, обусловленное поверхностным натяжением, пропорционально коэффициенту поверхностного натяжения и средней кривизне поверхности.
Средней кривизной называют выражение в скобках 1/R1+1/R2. В 1831 г. Карл Гаусс показал, что средняя кривизна поверхностей не зависит от ориентации сечений, в которых измерялись радиусы кривизны R1 и R2. Важно лишь, чтобы эти сечения были взаимно перпендикулярны. На практике ориентация сечений выбирается из соображений геометрической простоты.
Наиболее часто встречаются три случая.
а. Поверхность сферическая (капли, пузырьки). Радиус кривизны равен радиусу сферы, R1 = R2 = R, p = 2s| R.
б. Поверхность цилиндрическая. Одно сечение удобно взять нормально оси цилиндра, R1 = R, другое – в плоскости оси, R2 = ¥. Средняя кривизна цилиндрической поверхности 1/R + 1/¥ = 1/R, где R – радиус цилиндра, p = s| R.
 в. Плоская поверхность. Радиус кривизны в любом сечении R1 = R2 = ¥, кривизна равна нулю, давление Лапласа равно нулю.
в. Плоская поверхность. Радиус кривизны в любом сечении R1 = R2 = ¥, кривизна равна нулю, давление Лапласа равно нулю.
Если поверхность жидкости выпуклая, как, например, у капли, то лапласовское давление положительно, p > 0, жидкость дополнительно подпрессована (рис.64-а).
Если же поверхность вогнутая, как у воздушного пузырька в жидкости, то лапласовское давление отрицательно, p < 0, жидкость растягивается поверхностными силами (рис.64-б).
Отсюда ясно, что радиус кривизны поверхности – алгебраическая величина. Если центр кривизны поверхности находится со стороны жидкости, то радиус кривизны R – положительное число, R > 0. Если же центр кривизны поверхности находится со стороны газа, то R < 0.
2. Жидкость в круглом капилляре. Рассмотрим поведение жидкости в сосуде малых размеров, где поверхностные силы соизмеримы с объемными. Такие сосуды называются капиллярами (от лат. capillus – волос). Круглые капилляры – это полые цилиндры радиусом не более 1-5 мм.
Если жидкость смачивает стенки капилляра, она поднимается в нем вверх, если не смачивает – опускается вниз по сравнению с уровнем свободной плоской поверхности. Найдем высоту поднятия или опускания жидкости в круглом вертикальном капилляре.
На рис.65 показан случай смачивающей жидкости в капилляре радиусом r. Мениск смачивающей жидкости в круглом капилляре представляет собой сегмент сферы радиусом R. Этот сегмент, приподняв жидкость вверх по капилляру на высоту H, растягивает жидкость, создавая в ней отрицательное лапласовское давление.
По закону сообщающихся сосудов давление на уровне свободной поверхности h = 0 как вне, так и внутри капилляра одно и тоже. Снаружи оно равно атмосферному p0.
 Внутри капилляра (точка А) оно складывается из трех частей: атмосферного p0, лапласовского p = 2s /R и гидростатического rgH. Так что
Внутри капилляра (точка А) оно складывается из трех частей: атмосферного p0, лапласовского p = 2s /R и гидростатического rgH. Так что 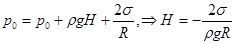 . (18.6)
. (18.6)
Радиус кривизны мениска R в случае смачивающей жидкости – отрицательное число. Он связан с радиусом капилляра r соотношением 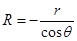 , (18.7)
, (18.7)
где q – краевой угол. Отсюда 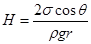 . (18.8)
. (18.8)
Здесь r – плотность жидкости, g – ускорение свободного падения.
По мере поднятия в капилляре внутрижидкостное давление будет уменьшаться за счет уменьшения гидростатического давления. В произвольной точке B на высоте h над уровнем свободной поверхности давление
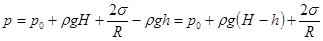 . (18.9)
. (18.9)
 Давление под мениском на высоте капиллярного подъема жидкости h = H складывается лишь из атмосферного и лапласовского. В смачивающей жидкости лапласовское давление отрицательно, поэтому давление под мениском меньше атмосферного на величину лапласовского давление, p = p0+2s| R = p0-rgH. (18.10)
Давление под мениском на высоте капиллярного подъема жидкости h = H складывается лишь из атмосферного и лапласовского. В смачивающей жидкости лапласовское давление отрицательно, поэтому давление под мениском меньше атмосферного на величину лапласовского давление, p = p0+2s| R = p0-rgH. (18.10)
Формула (18.8) пригодна и к случаям несмачивающей жидкости. В этом случае 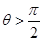 , cosq – отрицательное число. Поскольку все остальные величины r, r, g, s – положительные числа, то при cosq <0 и H будет отрицательным числом. Мениск несмачивающей жидкости опускается ниже уровня свободной поверхности (рис.66).
, cosq – отрицательное число. Поскольку все остальные величины r, r, g, s – положительные числа, то при cosq <0 и H будет отрицательным числом. Мениск несмачивающей жидкости опускается ниже уровня свободной поверхности (рис.66).
Давление непосредственно под мениском также определяется формулой (18.10) и больше атмосферного на величину лапласовского давления.
 Наиболее заметно капиллярное поднятие или опускание жидкости, когда диаметр капилляра меньше 1 мм. Например, вода в стеклянной трубке диаметром 2 мм поднимается на высоту
Наиболее заметно капиллярное поднятие или опускание жидкости, когда диаметр капилляра меньше 1 мм. Например, вода в стеклянной трубке диаметром 2 мм поднимается на высоту 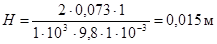 , а в капилляре диаметром 0,1 мм – на высоту около 0,30 м. Ртуть в капилляре диаметром 0,1 мм опускается на 14,5 см.
, а в капилляре диаметром 0,1 мм – на высоту около 0,30 м. Ртуть в капилляре диаметром 0,1 мм опускается на 14,5 см.
3. Жидкость в плоском капилляре. Плоским капилляром называется совокупность двух твердых плоских поверхностей, расположенных на близком расстоянии друг от друга. Различают плоскопараллельный капилляр с параллельными стенками и капиллярный клин.
а. Плоскопараллельный капилляр. Найдем высоту поднятия жидкости между двумя параллельными стенками (рис.67). Как и в круглом капилляре смачивающая жидкость поднимается между стенками вверх. Но ее свободная поверхность между стенками имеет форму цилиндра с радиусом кривизны R, который связан с шириной зазора a соотношением: 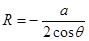 . (18.11)
. (18.11)
Так как лапласовское давление, создаваемое цилиндрической поверхностью, равно p = s /R, то высота H подъема жидкости в плоском капилляре 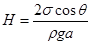 . (18.12)
. (18.12)
Если между двумя параллельными плоскостями имеется жидкость, то на каждую поверхность действует сила F = pS, где p = s /R – лапласовское давление, а S – площадь жидкого слоя. Так что 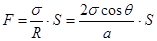 . (18.13)
. (18.13)
Если 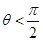 , поверхности стягиваются жидким слоем, при
, поверхности стягиваются жидким слоем, при 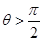 – отталкиваются.
– отталкиваются.
Например, две стеклянные пластинки площадью S = 10×10 см2, смоченные водой и находящиеся на расстоянии a = 0,01 мм друг от друга, стягиваются с силой
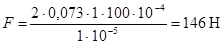 . Оторвать одну пластинку от другой довольно трудно, но они легко сдвигаются друг относительно друга.
. Оторвать одну пластинку от другой довольно трудно, но они легко сдвигаются друг относительно друга.
 б. Капиллярный клин возникает в области вершины двугранного угла, образованного двумя плоскими поверхностями (рис.68). Поскольку расстояние a между поверхностями по мере удаления от вершины O растет по закону a = a x, где a – двугранный угол, то высота подъема жидкости уменьшается,
б. Капиллярный клин возникает в области вершины двугранного угла, образованного двумя плоскими поверхностями (рис.68). Поскольку расстояние a между поверхностями по мере удаления от вершины O растет по закону a = a x, где a – двугранный угол, то высота подъема жидкости уменьшается,
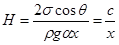 . (18.14)
. (18.14)
Здесь 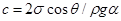 – постоянная для данного клина в данной жидкости величина.
– постоянная для данного клина в данной жидкости величина.
Уравнение H = c| x есть уравнение гиперболы, которую образует верхняя граница жидкости внутри двугранного угла.
4. Капиллярные явления. Хотя круглый и плоский капилляры являются идеализациями и в природе встречаются нечасто, закономерности, которые выявляются при их изучении, проявляются в капиллярах самых причудливых форм. Перечислим некоторые явления, имеющие капиллярную природу.
 а. Капиллярное перемещение жидкости. Если в сужающийся капилляр попадает капля смачивающей жидкости, то за счет разности кривизны свободных поверхностей возникает перепад давлений, смещающий каплю в более узкую область (рис.69).
а. Капиллярное перемещение жидкости. Если в сужающийся капилляр попадает капля смачивающей жидкости, то за счет разности кривизны свободных поверхностей возникает перепад давлений, смещающий каплю в более узкую область (рис.69).
Капля может перемещаться также в капилляре постоянного сечения, если со стороны одного мениска жидкость имеет более высокую температуру, чем со стороны другого. Разность давлений возникает в этом случае из-за разности поверхностного натяжения, в результате капля перемещается в более холодную область.
Капиллярное перемещение жидкости играет большую роль в живой природе и почве.
б. Капиллярная контракция – это уменьшение объема пористых тел при высушивании. Наиболее заметно капиллярная контракция проявляется при высушивании растительных стеблей – травы и древесины.
 Например, при просушке древесины влага, испаряясь из капилляров между волокнами целлюлозы, постепенно стягивается в область все более узких мест. В результате радиус кривизны менисков постепенно уменьшается, а отрицательное лапласовское давление увеличивается. Под действием внешнего давления волокна при высыхании сближаются и остаются в этом положении.
Например, при просушке древесины влага, испаряясь из капилляров между волокнами целлюлозы, постепенно стягивается в область все более узких мест. В результате радиус кривизны менисков постепенно уменьшается, а отрицательное лапласовское давление увеличивается. Под действием внешнего давления волокна при высыхании сближаются и остаются в этом положении.
5. Опытное определение коэффициента поверхностного натяжения s включает в себя более пяти различных методов. Наиболее просты в техническом исполнении и наглядны два из них: метод капель и метод капиллярного подъема.
 а. Метод капель. Из стеклянной трубки дают возможность жидкости медленно вытекать одиночными каплями (рис.71). Если допустить, что капля отрываeтся от трубки тогда, когда ее вес mg сравняется с силой поверхностного натяжения 2pr×s, удерживающей каплю в висячем положении, где r – радиус выходного конца трубки, то
а. Метод капель. Из стеклянной трубки дают возможность жидкости медленно вытекать одиночными каплями (рис.71). Если допустить, что капля отрываeтся от трубки тогда, когда ее вес mg сравняется с силой поверхностного натяжения 2pr×s, удерживающей каплю в висячем положении, где r – радиус выходного конца трубки, то 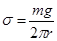 . (18.15)
. (18.15)
Здесь m – масса капли, g – ускорение свободного падения.
б. Метод капиллярного подъема основан на явлении втягивания смачивающей жидкости в капилляр или выталкивания несмачивающей жидкости из капилляра. Высота капиллярного подъема (опускания) определяется формулой (18.8).
Измерив диаметр капилляра 2r, плотность жидкости r и высоту капиллярного подъема (опускания) H, можно вычислить поверхностное натяжение s. Строго говоря, если жидкость неизвестная, и неизвестен краевой угол q при ее контакте с данной твердой поверхностью, то в этих методах определяется произведение s×cosq.
Краевой угол q может быть определен прямым его измерением на большой капле, помещенной на горизонтальную поверхность.
Жидкие растворы
1. Растворы – это макроскопические однородные смеси двух или большего числа веществ (компонентов), образующих термодинамически равновесные системы. В растворах все компоненты находятся в молекулярно-дисперсном состоянии. Они равномерно распределены в виде отдельных атомов, молекул, ионов или в виде групп из небольшого числа этих частиц. Различают газообразные, жидкие и твердые растворы. В данном параграфе речь пойдет о жидких растворах двухкомпонентного состава.
2. Концентрация растворов. Растворяться в жидкостях могут газы, жидкости и твердые тела. Взаимное растворение жидкостей может быть полным или частичным. Вода и спирт, например, растворяются друг в друге в любом соотношении, а вода и анилин растворяются частично.
Жидкость, взятая в большем количестве, называется растворителем. Другой компонент – растворяемым веществом. Для количественной характеристики соотношения между компонентами растворов используется понятие концентрации.
а. Весовая концентрация cm есть отношение массы растворенного вещества m1 к массе раствора m1+m2, где m2 – масса растворителя. 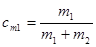 . (19.1)
. (19.1)
Обычно весовую концентрацию выражают в процентах. Например, 5%-й раствор йода, 40%-й раствор спирта, 70%-й раствор уксусной кислоты.
Для приготовления раствора нужной весовой концентрации исходной для расчетов величиной является масса необходимого раствора. Например, для приготовления m = 1 кг 10%-го раствора сахара надо взять m1 = cm1×m = 0,1×1 кг = 0,1 кг сахара и растворить его в m-m1 = 1-0,1 = 0,9 кг воды.
б. Молярная концентрация См выражается числом молей вещества, растворенного в единице объема раствора. 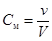 . (19.2)
. (19.2)
В системе единиц СИ единица измерения молярной концентрации Cм моль/м3. Для обычных растворов это очень малая концентрация. Поэтому в практических физико-химических исследованиях применяют более крупную единицу моль на литр. Очевидно 1 моль/л = 103 моль/м3.
При одномолярной концентрации в единице объема раствора содержится 1 моль растворенного вещества, содержащий число Авогадро NА частиц.
В общем случае, если известна молярная концентрация раствора См, то известна и концентрация частиц n растворенного вещества, n = См×NА. (19.3)
Поэтому молярная концентрация удобна не только в лабораторной практике, но и в теоретических исследованиях. Для приготовления растворов с известной молярной концентрацией в мерную колбу объемом V помещается вначале известное число v молей растворяемого вещества, а затем заливается растворитель до метки.
в. Молярная доля cn. В случае молярной концентрации Cм неизвестна концентрация в растворе молекул растворителя. Это приемлемо в тех случаях, когда растворитель пассивный и не участвует в физико-химическом процессе. Если же количество растворителя должно быть известно, используют молярную долю cn. 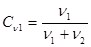 . (19.4)
. (19.4)
Здесь n1 – число молей растворенного вещества, n2 – число молей растворителя. Оба этих вещества выступают здесь как равноправные компоненты, число которых не ограничено. Молярная доля растворителя 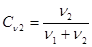 . (19.5)
. (19.5)
Молярная доля раствора - это соотношение между числом молекул растворенного вещества и растворителя. Например, в растворе спирта с его молярной долей cn1 = 0,2 на 4 молекулы воды приходится одна молекула спирта. 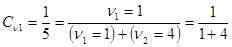 .
.
Переход от весовой концентрации cm к молярной Cм и молярной доле cn можно выполнить с использованием формул: 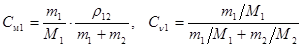 . (19.6)
. (19.6)
Здесь m1 + m2 = m – масса раствора, r12 – его плотность, M1 и M2 – молярные массы компонент. Очевидно, m1 = cm1×m, m2 = cm2×m.
3. Растворимость веществ. Раствор, содержащий наибольшее количество вещества, которое может в нем раствориться, называется насыщенным. Если концентрация растворенного вещества меньше, чем в насыщенном растворе, то раствор называется ненасыщенным. Если концентрация больше, раствор называется перенасыщенным. Перенасыщенные растворы метастабильны. При появлении зародышей избыток растворенного вещества выпадает из раствора, и раствор становится насыщенным.
Концентрация насыщенного раствора есть мера растворимости, то есть способности вещества растворяться в растворителе. Растворимость выражают обычно в граммах вещества, растворяющегося в 100 граммах растворителя. Например, растворимость в воде при 20°C сахара составляет 20,4 г, поваренной соли – 36,0 г, соды Na2CO3 – 21,5 г, нитрата серебра AgNO3 – 222 г.
4. Растворение в жидкостях газов, молекулы которых химически не взаимодействуют между собой и с молекулами растворителя, подчиняется закону Генри: при постоянной температуре растворимость газа пропорциональна парциальному давлению его над раствором (Уильям Генри, 1903 г.). m = kp. (19.7)
Здесь m – масса растворенного газа, p – его парциальное давление над растворителем, k – коэффициент, который зависит от природы газа, растворителя и температуры.
Закон Генри применим к идеальным плохо растворимым газам, например, к азоту, кислороду, водороду, гелию и др. Для аммиака NH3 и углекислого газа CO2, хорошо растворяющихся в воде, закон Генри неприменим.
5. Теплота растворения. Растворение вещества в жидкостях является результатом взаимодействия частиц растворяемого вещества с частицами растворителя. Поскольку растворение – это разделение частиц растворяемого вещества, которые были связаны между собой силами притяжения, то оно требует затраты энергии.
Против сил притяжения должна быть совершена работа, и она совершается силами взаимодействия между частицами растворяемого вещества и растворителя.
Энергию растворения 1 моля вещества в настолько большом количестве растворителя, чтобы частицы растворенного вещества не взаимодействовали между собой, называют молярной теплотой растворения Qp. Эта теплота поглощается из раствора, в результате температура раствора в процессе растворения может понижаться.
Нередко молекулы или ионы растворенного вещества образуют с молекулами растворителя довольно устойчивые комплексы – сольваты (от лат. solvo – растворяю). Так как сольваты обладают меньшей потенциальной энергией по сравнению с молекулами чистого растворителя, то процесс сольватации сопровождается выделением энергии Qs.
В результате этих двух процессов растворение вещества может сопровождаться как поглощением энергии, Qp > Qs, температура раствора понижается, так и выделением энергии, Qp < Qs, температура раствора повышается.
В таблице 19 приведены значения суммарной теплоты растворения Q = Qp + Qs в воде при температуре T для некоторых веществ.
| Таблица 19 | |||||
| Вещество | T, K | Q, кДж/моль | Вещество | T, K | Q, кДж/моль |
| NaOH, твердый NaCl, твердый Na2CO3, твердый NaHCO3, твердый KOH, твердый NH4NO3, твердый MgSO4×7H2O, твердый | +41,6 -4,9 +23,6 -18,0 +55,6 -26,4 -15,9 | ZnSO4, твердый CuSO4×H2O, твердый CuSO4×5H2O, твердый HCl, газ H2SO4, жидкая HNO3, жидкая CH3COOH, жидкая | +77,0 +39,0 -11,5 +72,5 +74,7 +31,3 +1,4 |
Существуют такие растворы, в которых Qp = Qs. Тепловой эффект у них отсутствует, DT = 0. Обычно это близкие по химическим свойствам вещества. Например CH3-OH и C2H5-OH, бензол и толуол, бензин и керосин. Это так называемые идеальные растворы.
Растворимость веществ, теплота растворения которых отрицательна Q < 0, с повышением температуры растет. Например, растворимость в воде AgNO3, у которого Q = - 22,7 кДж/моль, в интервале температур от 0 до 100°C увеличивается с 122 до 952 г.
Относительно твердых веществ, растворяющихся с выделением теплоты, обратное утверждение нельзя сделать однозначно. Дело в том, что выделение теплоты есть результат химического взаимодействия молекул растворителя с молекулами растворяемого вещества. Во многих случаях с ростом температуры происходит частичное разрушение сольватных комплексов. Поэтому нередко растворимость и этих веществ с ростом температуры повышается. Например, растворимость соды Na2CO3 (Q = +23,6 кДж/моль) в интервале температур 0-100°C увеличивается в 8 раз. Но есть и обратные случаи. Растворимость извести Ca(OH)2 (Q = +11,7 кДж/моль) падает с 0,185 г до 0,077 г.
Все газы растворяются с выделением тепла, Q > 0. Растворимость всех газов с ростом температуры уменьшается.
 6. Осмос. (от греч. osmos – толчок, давление) – диффузия растворителя через полупроницаемую мембрану, разделяющую раствор и чистый растворитель.
6. Осмос. (от греч. osmos – толчок, давление) – диффузия растворителя через полупроницаемую мембрану, разделяющую раствор и чистый растворитель.
Пусть слева от мембраны – чистый растворитель A, а справа – раствор A + B (рис.72). Молекулы A могут свободно проходить слева направо и справа налево. Но размер молекул B больше размера отверстий в мембране, поэтому молекулы B не проходят из раствора в чистый растворитель. Так как концентрация молекул растворителя A слева больше, чем справа, то и поток диффузии молекул A слева больше, чем справа. В результате уровень раствора справа повышается. Это продолжается до тех пор, пока потоки диффузии слева и справа не уравновесятся.
Количественной характеристикой осмоса является осмотическое давление. Величина его равна тому давлению, которое, будучи приложенным к раствору, уравновешивает потоки диффузии молекул растворителя слева и справа. В 1887 г. нидерландский физико-химик Якоб Вант-Гофф открыл закон, определяющий зависимость осмотического давления П от концентрации и температуры раствора. П = vRT| V. Вант-Гофф, 1887 (19.8)
Здесь v | V – молярная концентрация раствора (v – число молей вещества, растворенного в объеме V раствора), T – температура, R = 8,31 Дж/(моль×K) – газовая постоянная.
По закону Вант-Гоффа, осмотическое давление, создаваемое растворенным веществом, равно давлению, которое производило бы это вещество, будучи в газообразном состоянии в том же объеме, при той же температуре и в том же структурном составе.
Закон Вант-Гоффа лучше выполняется для растворов малых концентраций, когда отсутствует взаимодействие между молекулами растворенного вещества. Осмотическое давление не зависит от вида полупроницаемой мембраны, от рода растворителя и от особенностей растворенного вещества. Лишь бы его молекулы не проходили сквозь мембрану.
Величина осмотического давления значительна. Например, раствор сахара в воде, молярная концентрация которого Cм = 0,1 моль/л, создает осмотическое давление П = nRT| V = 0,1×8,31×293/10-3 = 2,43×105 Па.
7. Осмос в электролитах. В растворах кислот, солей и щелочей осмотическое давление оказалось больше, чем это следует из формулы (19.8). Выходило, что число частиц в электролитах больше числа молекул растворенного вещества. Поэтому Вант-Гофф ввел в свой закон для электролитов поправочный множитель i (изотонический коэффициент), который показывает, во сколько раз наблюдаемое осмотическое давление больше вычисленного по формуле (19.8). П = inRTçV. (19.9)
Дело в том, что молекулы солей, кислот и щелочей в растворах распадаются на ионы, говорят, диссоциируют. Например, NaCl « Na+ + Cl-, HCl « H+ + Cl-=, NaOH « Na+ + OH-. Доля молекул, распавшихся на ионы, называется степенью диссоциации и обозначается a. Общее увеличение числа частиц растворенного вещества i = 1+a. Формула закона Вант-Гоффа принимает вид: П = (1 + a)nRTçV. (19.10)
Она применима как к электролитам (a > 0), так и к неэлектролитам (a = 0).
8. Осмос в живой природе играет исключительно важную роль. Осмос лежит в основе корневой системы питания растений. В результате фотосинтеза в них вырабатываются крупные молекулы органических кислот, сахаров и других соединений, которые и создают внутри растений осмотическое давление. Роль полупроницаемой мембраны играет корневая система, которая всасывает воду с мелкими молекулами неорганических веществ. Последние нужны как строительные элементы для синтеза необходимых растению органических веществ. Благодаря осмосу влага в растениях удерживается на высоте в десятки метров.
Питание представителей царства животных также происходит благодаря осмосу. Кровь и лимфа животных – это растворы органических и неорганических веществ. Если осмотическое давление в пищеварительном тракте ниже, чем в крови, влага с питательными веществами всасывается в кровь. Если осмотическое давление в крови по каким-то причинам оказалось ниже, чем в кишечнике (животное объелось соли), всасывание меняет направление, организм обезвоживается, животное погибает.
9. Поверхностное натяжение растворов зависит от концентрации растворов и от вида растворенного вещества. Наибольшее практическое значение имеют водные растворы.
При растворении в воде неорганических электролитов – кислот, солей и щелочей – поверхностное натяжение раствора увеличивается по линейному закону: s = s0+kCм, (19.11)
где s0 – поверхностное натяжение чистой воды, Cм – молярная концентрация раствора, k – коэффициент.
В таблице 20 приведены значения k для некоторых солей при температуре 20°C. Численные значения k соответствуют приросту поверхностного натяжения при увеличении концентрации на 1 моль/м3.
| Таблица 20 | |
| Соль | k, 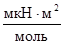
|
| KCl NaCl Na2CO3 NaNO3 Na2SO4 | 1,4 1,6 1,3 1,2 1,4 |
Вещества, повышающие поверхностное натяжение, называются поверхностно-инактивными.
Растворение органических веществ – мыл, спиртов, жирных кислот – обычно понижает поверхностное натяжение. Вещества этой группы называются поверхностно-активными (ПАВ). Молекулы ПАВ построены из двух частей – полярной, гидрофильной группы, имеющей сродство к воде (COOH, OH, NH2, NO2) и неполярного радикала, с которым связана пониженная растворимость ПАВ в воде.
 Понижение s в растворах ПАВ сопровождается повышением концентрации их молекул в поверхностном слое по сравнению с объемной концентрацией. Это явление называется адсорбцией (от лат. ad – на, sorbeo – поглощаю).
Понижение s в растворах ПАВ сопровождается повышением концентрации их молекул в поверхностном слое по сравнению с объемной концентрацией. Это явление называется адсорбцией (от лат. ad – на, sorbeo – поглощаю).
При малой концентрации адсорбированных молекул тепловое движение нарушает их ориентацию, и молекулы в основном лежат в поверхностном слое (рис.73-а). С повышением концентрации взаимодействие углеводородных цепей между собой усиливается, это способствует их вертикальной ориентации (рис.73-б). При насыщении адсорбционного слоя образуется мономолекулярный слой ориентированных молекул (рис.73-в).
 Образование адсорбционного слоя полярных молекул позволяет использовать растворы ПАВ в качестве моющих средств. Полярные молекулы обволакивают частицы загрязнений и переносят их в раствор в качестве фрагментов эмульсий.
Образование адсорбционного слоя полярных молекул позволяет использовать растворы ПАВ в качестве моющих средств. Полярные молекулы обволакивают частицы загрязнений и переносят их в раствор в качестве фрагментов эмульсий.
Адсорбция полярных молекул ПАВ не только понижает поверхностное натяжение жидкости, но и существенно стабилизирует поверхность, позволяя получать устойчивые двусторонние тонкие пленки типа мыльных пузырей. Толщина таких пленок не может быть меньше удвоенного радиуса 2r действия сил межмолекулярного притяжения (рис.74). При толщине пленки меньше 2r отрицательная энергия молекулярного взаимодействия в середине пленки будет убывать по абсолютной величине, разница между энергиями молекул в глубине и в поверхностном слое будет уменьшаться, и система перестанет быть устойчивой.
Реальная минимальная толщина пленок колеблется около 1 мкм, что составляет от нескольких сотен до нескольких тысяч поперечников молекул жидкости.
6.Принцип Ле-Шателье-Брауна. Для качественной оценки изменений в равновесной системе, происходящих при внешнем взаимодействии, в термодинамике широко применяется принцип подвижного равновесия. Он гласит: если на систему, находящуюся в равновесии, направить внешнее воздействие, нарушающее равновесие, в ней самопроизвольно происходят изменения в направлении уменьшения этого воздействия.
Этот принцип открыл в 1884 г. Анри Ле-Шателье, обобщая частные закономерности, а Карл Браун обосновал его на основе 2-го закона термодинамики в 1888 г.
В отличие от 2-го закона термодинамики, также указывающего направление самопроизвольно протекающих процессов и являющегося эффективным методом количественного исследования систем, принцип Ле-Шателье-Брауна носит качественный характер.
Примером действия принципа Ле-Шателье-Брауна может служить увеличение растворимости газов с ростом давления. Когда давление газа над жидкостью за счет внешнего воздействия увеличивается, система переводит часть газа в жидкость, тем самым ослабляя внешнее воздействие, растворимость газа растет. Если давление газа над жидкостью понижать, то система выделяет обратно часть газа из жидкости, стремясь к тому, чтобы понижение давления было как можно меньше. Растворимость газа уменьшается.
Принцип Ле-Шателье-Брауна имеет общефизический характер. Примером может служить правило Ленца, определяющее направление индукционного тока.
Дата добавления: 2020-05-20; просмотров: 1388;











