Уравнения Лагранжа второго рода.
Рассмотрим движение 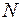 тел с геометрическими стационарными связями и
тел с геометрическими стационарными связями и 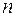 степенями свободы.
степенями свободы.
Для вывода уравнений Лагранжа кинетическую энергию Т системы 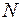 тел выразим через обобщенные координаты
тел выразим через обобщенные координаты 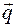 и обобщенные скорости
и обобщенные скорости 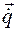 системы в виде:
системы в виде:
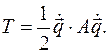
Вывод уравнений Лагранжа произведем из принципа Даламбера – Лагранжа. Напомним, что при этом, связи идеальны, а элементарная работа активных сил представима в виде:
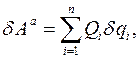
где 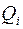 есть обобщенные силы системы.
есть обобщенные силы системы.
Принцип Даламбера – Лагранжа используем в следующем виде:
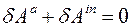 или
или 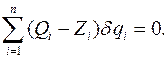
Вычислим элементарную работу сил инерций системы.
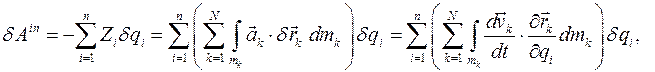
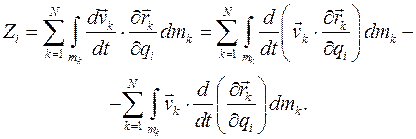
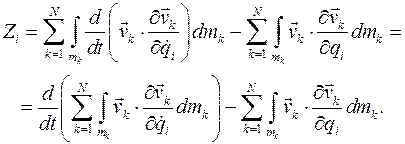
Из определения кинетической энергии 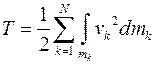 видно, что
видно, что
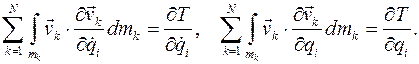
Окончательно уравнение Лагранжа принимает следующий вид:
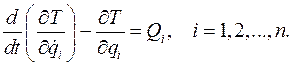
Консервативная система. Все активные силы потенциальны, связи стационарны (уравнения связей не зависят явно от времени). Потенциальная энергия 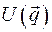 системы равна сумме потенциальных энергий всех активных сил.
системы равна сумме потенциальных энергий всех активных сил.
Определение. Функцию 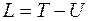 называют функцией Лагранжа.
называют функцией Лагранжа.
Так как в консервативной системе обобщенные силы выражаются через потенциальную энергию
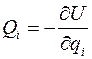 ,
,
то уравнения Лагранжа с помощью функции Лагранжа можно записать в виде:
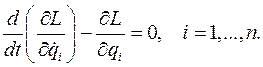
Дата добавления: 2020-05-20; просмотров: 771;











